Презентация на тему: Функции y=tg x и y=ctg x, их свойства и графики

Функции y=tg x и y=ctg x, их свойства и графики

Цели урока Научиться строить график функции y = tg x и y = ctg xИзучить свойства данных функций
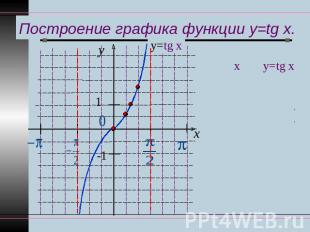
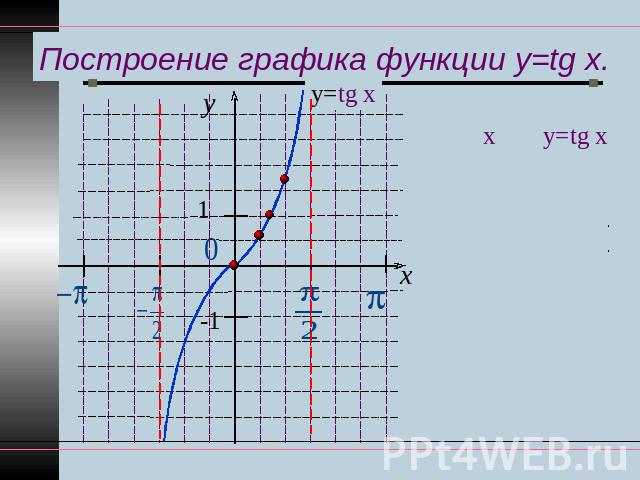
Построение графика функции y=tg x.
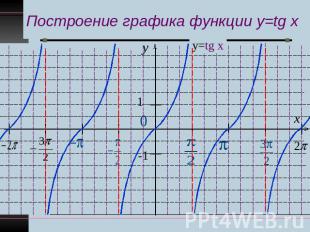
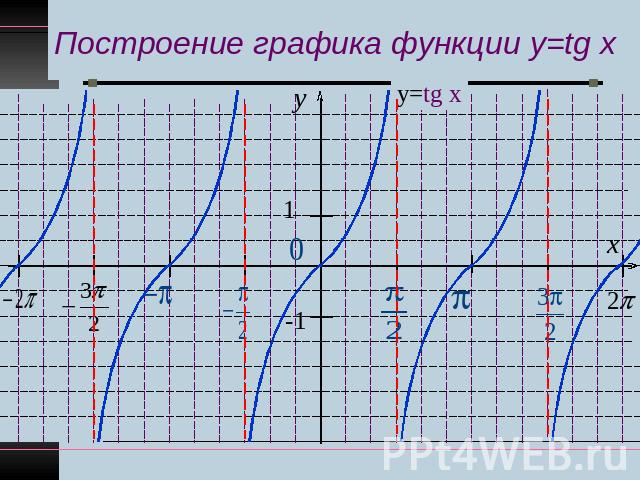
Построение графика функции y=tg x
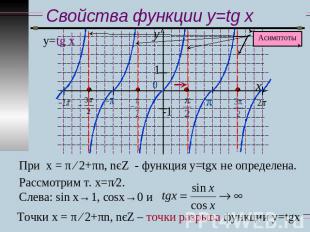
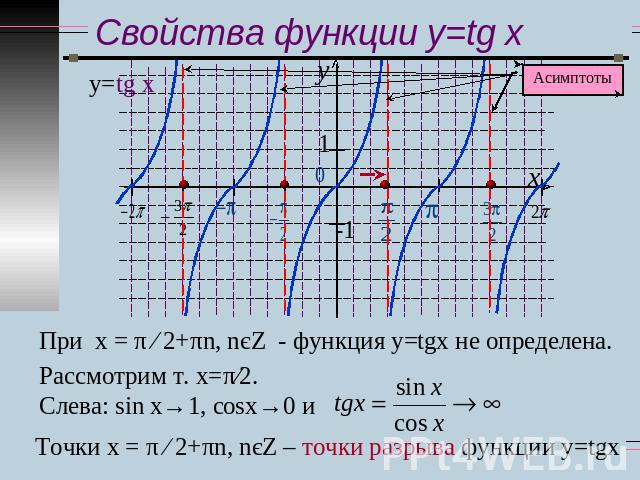
Свойства функции y=tg x При х = π ∕ 2+πn, nєZ - функция у=tgx не определена. Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx

Свойства функции y=tg x 1. Обл. определения: 2. Множество значений функции: уєR3. Периодическая, Т= π 4. Нечётная функция 5. Возрастает на всей области определения6. Нули функции у (х) = 0 при х = πn, nєZ7. у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ8. у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ9. При х = π ∕ 2+πn, nєZ - функция у=tgx не определена Имеет точки разрыва графика и асимптоты

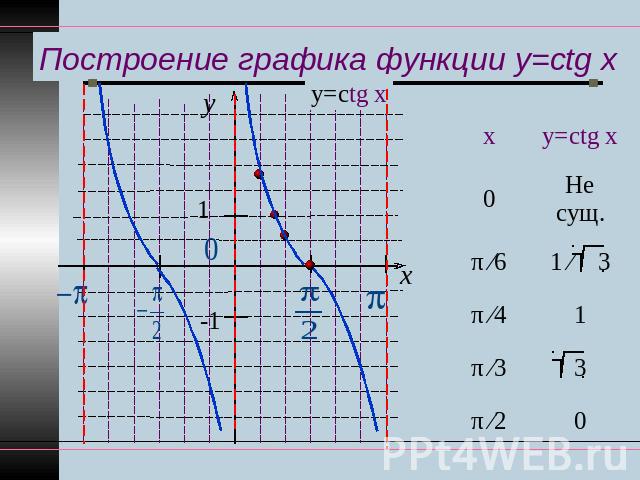
Функция y=ctg x, ее свойства и график
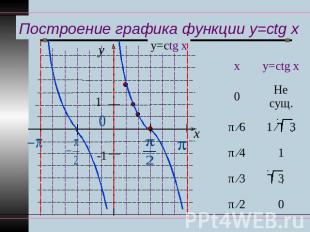
Построение графика функции y=ctg x