Презентация на тему: Теорема Пифагора

Устная работа Устная работа

Найдите гипотенузу. Найдите гипотенузу.

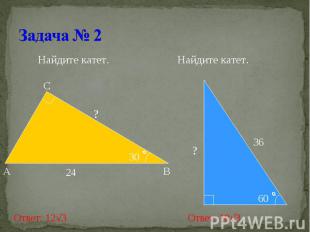
Найдите катет. Найдите катет.

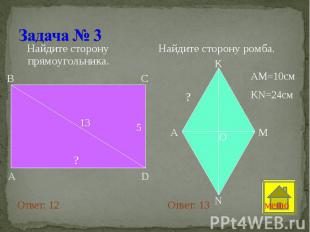
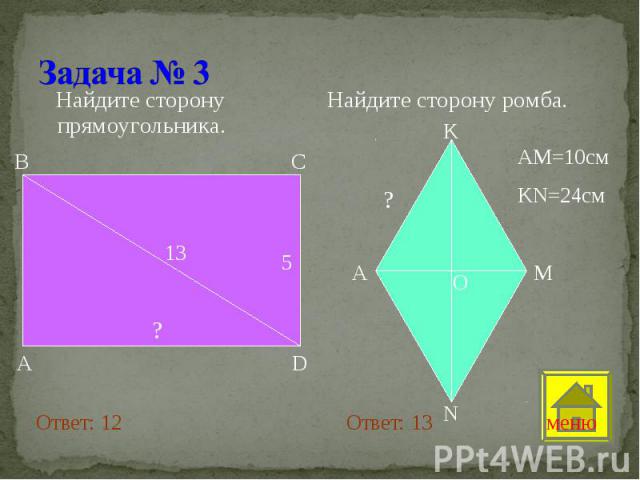
Найдите сторону прямоугольника. Найдите сторону прямоугольника.

I Вариант I Вариант 1)Катеты 8 и 15 см. Найти гипотенузу 2)Гипотенуза 61 см, катет 11 см. Найти другой катет 3)Диагональ прямоугольника 15 см, одна из сторон – 9 см. Найти его периметр

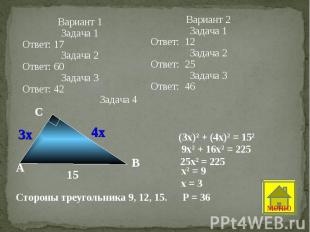
1. Построим треугольник ABC с прямым углом С. 1. Построим треугольник ABC с прямым углом С.

6. Четырехугольники ADFB и ACBE равновелики. Треугольники ABF и ЕCB равны. Значит треугольники ADF и ACE тоже равны. 7. Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2 8. Соответственно: а2+ b 2 =с 2

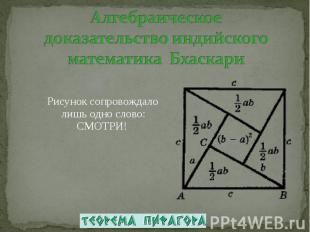
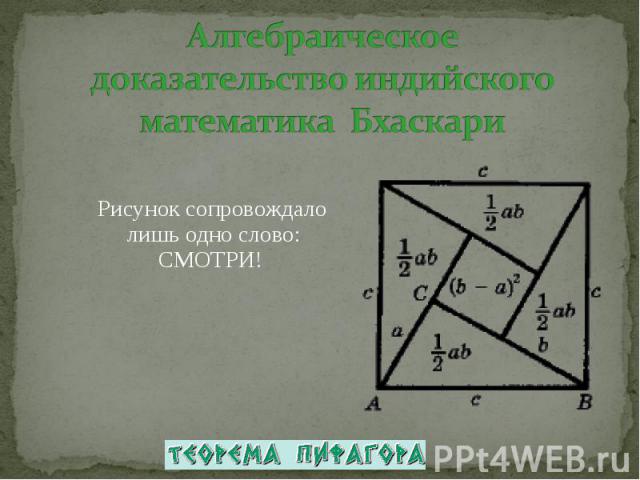
Рисунок сопровождало лишь одно слово: СМОТРИ! Рисунок сопровождало лишь одно слово: СМОТРИ!

1. Площадь данного треугольника АВС с одной стороны равна 0,5ab, 1. Площадь данного треугольника АВС с одной стороны равна 0,5ab, с другой 0,5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r=0,5(a+b-c)).

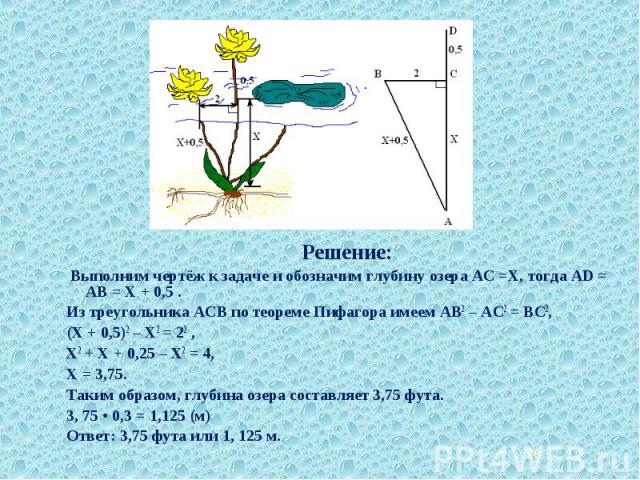
Над озером тихим Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс его в сторону. Нет Боле цветка над водой. Нашёл же рыбак его Ранней весною В двух футах от места, где рос. Итак, предложу я вопрос: “Как озера вода здесь глубока?”

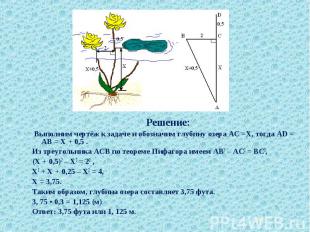
 Решение:  Решение: Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 . Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2, (Х + 0,5)2 – Х2 = 22 , Х2 + Х + 0,25 – Х2 = 4, Х = 3,75. Таким образом, глубина озера составляет 3,75 фута. 3, 75 • 0,3 = 1,125 (м) Ответ: 3,75 фута или 1, 125 м.

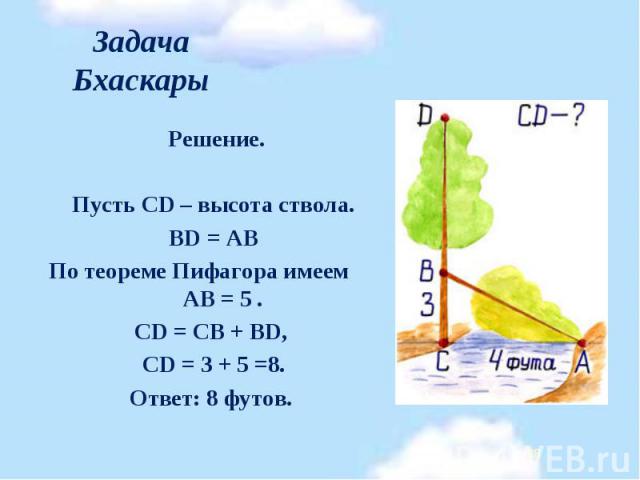
Решение. Решение.   Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ = 5 . CD = CB + BD, CD = 3 + 5 =8. Ответ: 8 футов.