Презентация на тему: Теорема Пифагора 2

Введение Введение Биография Пифагора Простейшее доказательство теоремы Древнекитайское доказательство Доказательство Евклида Доказательство теоремы Пифагора Еще одно алгебраическое доказательство Египетский треугольник Заключение Список литературы Авторы

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. Теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций.

Пифагор родился около 570 г. до н.э. на острове Самосе. Пифагор родился около 570 г. до н.э. на острове Самосе. В юности Пифагор отправляется в Милет, где встречается с ученым Фалесом, который советует ему отправится за знаниями в Египет. В 548 г. до н.э. Пифагор прибыл в самосскую колонию. Изучив язык и религию египтян, он уезжает в Мемфис. Жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания, но Пифагор преодолел их все. Научившись всему, что дали ему жрецы, он двинулся на родину в Элладу. Однако, проделав часть пути, его захватил в плен царь Вавилона. Вавилонская математика была более развитой, чем египетская, и Пифагору было чему поучится, позже он сбежал на родину. На родине Пифагор учредил нечто вроде религиозно-этического братства. ...Прошло 20 лет. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, он поджигает дом Пифагора. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор покончил жизнь самоубийством.

В прямоугольном треугольнике В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c²=a²+b²

“Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах” “Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах” Рассмотрим равнобедренный прямоугольный треугольник (с него и начиналась теорема). Достаточно посмотреть на мозаику равнобедренных прямоугольных треугольников. Для ABC квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по 2.

Рассмотрим рис.1: Рассмотрим рис.1: а+b - сторона внешнего квадрата, с - сторона внутреннего. Если вырезать внутренний квадрат (рис.1) со стороной с и уложить части его как показано на рис.2, получим: c²=a²+b²

Дано: ∆АВС-прямоугольный, а,b-катеты, с-гипотенуза, Дано: ∆АВС-прямоугольный, а,b-катеты, с-гипотенуза, ABHF, AGKC, BCED-квадраты Доказать: c²=a²+b² Доказательство: 1. ∆ABD=∆FBC(по 2-м сторонам и углу м/у ними) BC=BD FB=AB ∟DBА=90 +∟ABC=∟FBC 2. S∆ABD=1∕2SBYLD BD- общее основание, LD- общая высота 3. S∆FBC = 1∕2 SABFY (аналогично 2) 4. SABFH = SBYLD, т.к. ∆ABD=∆FBC 5. SACKG= SYCEL , т.к. ∆BCK=∆ACE(аналогично 1-4) 6. b²+a²=c² => c²=a²+b².

Дано: треугольник АВС - Дано: треугольник АВС - прямоугольный a, b - катеты с-гипотенуза Доказать: c2=a2+b2 Доказательство: 1. (a + b)2 = 4(1/2ab) + c2 2. a2 + 2ab + b2 = 2ab + c2 3. a2 + b2 = c2

Дано: ∆АВС – прямоугольный, ∟С=90º Дано: ∆АВС – прямоугольный, ∟С=90º Доказать: АС²+СВ²=АВ² Доказательство: 1.CD-высота. 2. cosА=AD/AC=AC/AB =>AD∙AB=AC² 3. cosB=BD/BC=BC/AB =>AB∙BD=BC² 4. Получим : AD∙AB+AB∙BD=AC²+BC² AB(AD+BD)=AC²+BC² AB²=AC²+BC²

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками: Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками: 3, 4 и 5 5, 12 и 13 8, 15 и 17 7, 24 и 25

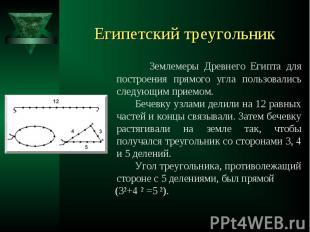
Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Бечевку узлами делили на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, чтобы получался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой (3²+4 ² =5 ²).

В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней. В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.

Шевцова Наталья Александровна, Шевцова Наталья Александровна, учитель математики высшей категории