Презентация на тему: РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ


Цель Цель В ходе изучения темы учащиеся должны знать,что множество решений системы неравенств есть пересечение множеств решений неравенств, входящих в эту систему 2) Научить решать системы, составленные из двух линейных неравенств.

Повторение Повторение Математический диктант Изучение нового материала Закрепление Итог урока
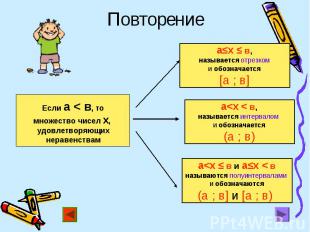
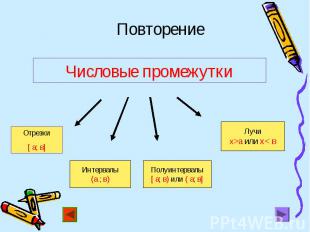

Запишите числовой промежуток, служащий множеством решений неравенства Запишите числовой промежуток, служащий множеством решений неравенства
![[3;6], [3;6], [1,5;5] [3;6], [3;6], [1,5;5]](https://fs1.ppt4web.ru/images/95581/140944/310/img6.jpg)
[3;6], [3;6], [1,5;5]
![Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых](https://fs1.ppt4web.ru/images/95581/140944/310/img7.jpg)
Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)?

0,1,2,3 0,1,2,3 -6,-5,-4,-3,-2,0

Укажите наибольшее и наименьшее целое число, принадлежащее промежуткам Укажите наибольшее и наименьшее целое число, принадлежащее промежуткам (-8; 8), (-6;-2)

Наибольшее 7 Наибольшее 7 Наименьшее -7 Наибольшее -3 Наименьшее -5

Записать неравенства, множеством решения которых служат промежутки Записать неравенства, множеством решения которых служат промежутки


Чтобы решить систему линейных неравенств, достаточно решить каждое из входящих в неё неравенство и найти пересечение множеств их решений. Чтобы решить систему линейных неравенств, достаточно решить каждое из входящих в неё неравенство и найти пересечение множеств их решений.

5Х-1 > 3( Х+ 1), 2(Х+4) > Х+5 Решим первое неравенство 5Х-1.> 3Х+3, 2Х > 4, Х > 2 Решим второе неравенство 2Х+8 > Х+ 5, Х > -3

Решение 1 неравенства все точки Решение 1 неравенства все точки луча Х > 2 Решение 2 неравенства все точки луча Х > -3
![3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7 4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4 [4;7] 3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7 4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4 [4;7]](https://fs1.ppt4web.ru/images/95581/140944/310/img16.jpg)
3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7 4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4 [4;7]

Рассмотрены примеры решения систем линейных неравенств. Рассмотрены примеры решения систем линейных неравенств. Учащиеся научились показывать множество решений систем линейных неравенств на координатной прямой.




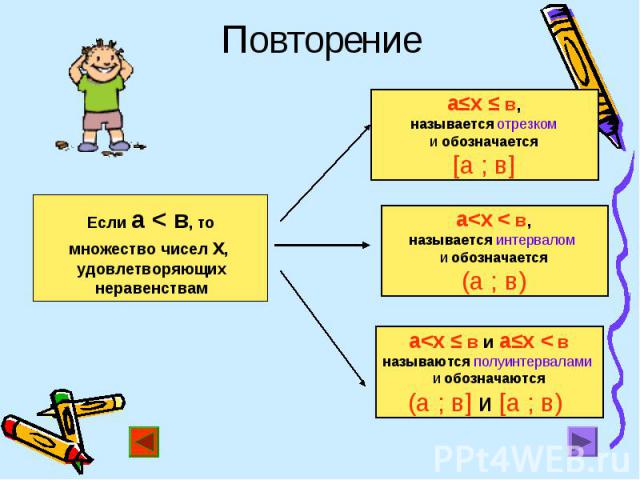
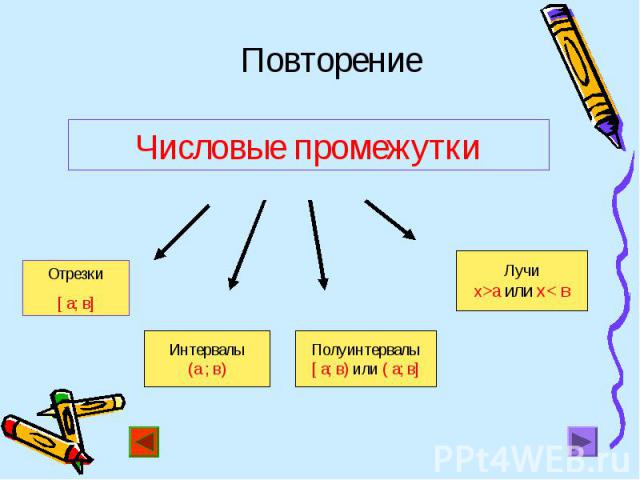

![[3;6], [3;6], [1,5;5] [3;6], [3;6], [1,5;5]](https://fs1.ppt4web.ru/images/95581/140944/640/img6.jpg)
![Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)? Какие из целых чисел принадлежат промежутку (-1; 3,6], [-6,6;1)?](https://fs1.ppt4web.ru/images/95581/140944/640/img7.jpg)




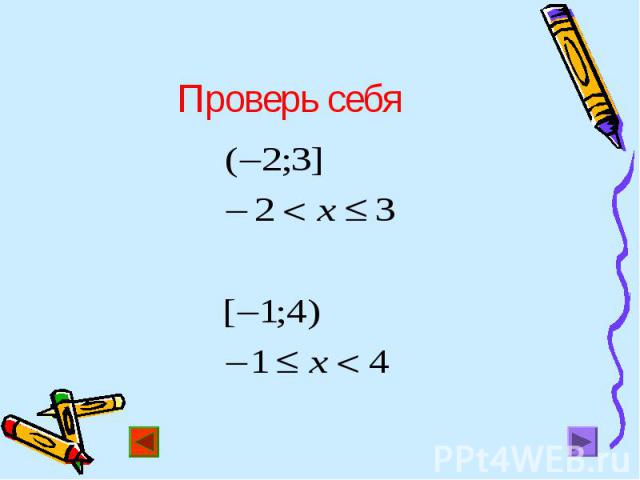



![3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7 4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4 [4;7] 3(Х-1) ≤ 2Х + 4, 3Х-3 ≤2Х+4, Х ≤ 7 4Х-3 ≥ 13; 4Х ≥ 16 ; Х ≥ 4 [4;7]](https://fs1.ppt4web.ru/images/95581/140944/640/img16.jpg)












