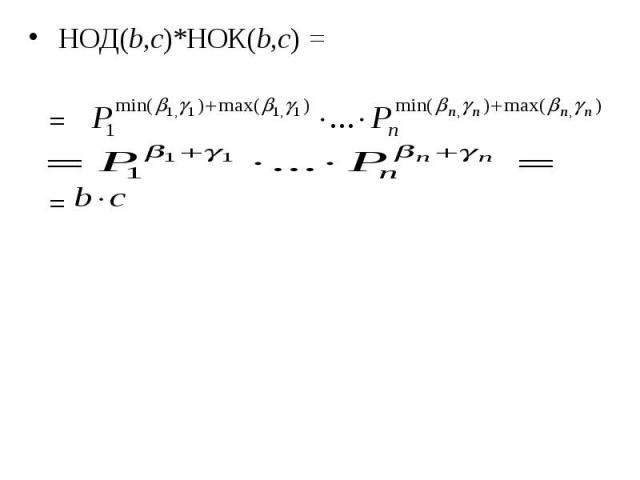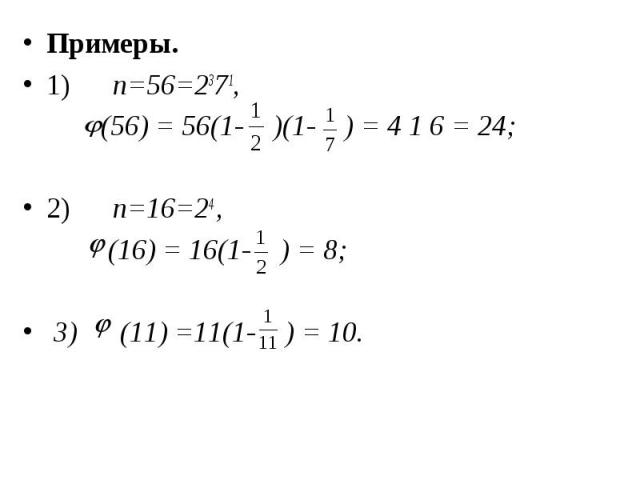Презентация на тему: Некоторые теоретико-числовые приложения комбинаторики

§5. Некоторые теоретико-числовые приложения комбинаторики §5. Некоторые теоретико-числовые приложения комбинаторики Определение 1. Натуральное число называется простым, если оно имеет ровно два разных делителя: 1 и само себя. Натуральное число называется составным, если оно имеет более двух различных делителей.

Примеры. Числа 2, 3, 5, 7, 11 простые, числа 4, 6, 18, 100 составные. Отметим, что число 1 не является ни простым, ни составным. Примеры. Числа 2, 3, 5, 7, 11 простые, числа 4, 6, 18, 100 составные. Отметим, что число 1 не является ни простым, ни составным. Существует стандартная система обозначений простых чисел: Р1 – первое по величине простое число (ясно, что Р1 = 2), Р2 – следующее простое число, (Р2 = 3), (Р3 = 5), (Р4 = 7), (Р5 = 11), (Р6 = 13), (Р7 = 17), (Р8 = 19) и т.д. Вообще Рn – n-ое простое число. К сожалению, не существует аналитической формулы f (n), которая позволила бы вычислять любое простое число Pn.

Теорема 2. Простых чисел существует бесконечно много. Теорема 2. Простых чисел существует бесконечно много. Доказательство. Допустим, существует лишь конечное число простых чисел. Перечислим их: P1, Р2, …, РN. Значит, любое другое натуральное число содержит в качестве делителя по крайней мере одно из Рi (i = 1, 2, …, N). Рассмотрим число Р = Р1 Р2 … РN + 1. Очевидно, что это число не делится ни на одно из чисел

так как при делении на любое из этих чисел Р дает в остатке 1. так как при делении на любое из этих чисел Р дает в остатке 1. Значит, допущение о конечности множества простых чисел неверно. Простых чисел существует бесконечно много. Замечание. По дошедшим до нас историческим источникам это доказательство принадлежит Евклиду и является первым примером в математике доказательства «методом от противного». Простые числа являются «кирпичиками» из которых строятся все остальные натуральные и целые числа, отличные от 0, -1, 1.

Теорема3. (основная теорема арифметики). Для любого натурального числа а ≠ 1 имеет место равенство Теорема3. (основная теорема арифметики). Для любого натурального числа а ≠ 1 имеет место равенство а = для некоторых неотрицательных целых α1, α2, …, αк и натурального k. Правая часть равенства называется разложением числа а в произведение простых чисел. Такое разложение при фиксированной нумерации множества простых чисел единственно.

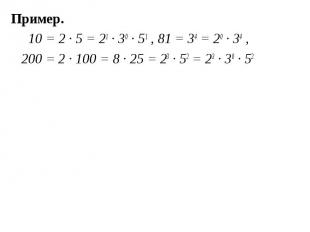
Пример. Пример. 10 = 2 ∙ 5 = 21 ∙ 30 ∙ 51 , 81 = 34 = 20 ∙ 34 , 200 = 2 ∙ 100 = 8 ∙ 25 = 23 ∙ 52 = 23 ∙ 30 ∙ 52.

Определение 4. Пусть а,b N. Число с называется общим делителем а и b , если оба они делятся на с без остатка. Определение 4. Пусть а,b N. Число с называется общим делителем а и b , если оба они делятся на с без остатка. Примеры. Пусть а = 24, b = 36. Тогда общими делителями a и b будут числа 1, 2, 3, 4, 6 и 12. Число 8 не будет общим делителем чисел 24 и 36. Пусть а = 10, b = 30. Общие делители – 1, 2, 5. Пусть а = 16, b = 35. Общий делитель, равный 1, единственный.

Теорема 5. Пусть  Теорема 5. Пусть  и  Число b является делителем а в том и только в том случае, когда βi ≤ αi для любого i = 1,…, n.

Следствие 6. Следствие 6. Пусть для натурального числа а имеет место равенство Тогда число делителей а вычисляется по формуле (α1 + 1) ∙ (α2 + 1) ∙ … ∙ (αn + 1).

Теорема 7. Пусть Теорема 7. Пусть и Тогда число является общим делителем чисел а и b в том и только в том случае, когда γ1 ≤ min (α1, β1), γ2 ≤ min (α2, β2), …, γn ≤ min (αn, βn).

Определение 8. Определение 8. Число c называется наибольшим общим делителем чисел а и b (обозначение: с = НОД (а, b)), если с является самым большим из всех общих делителей чисел а и b. Примеры. Пусть а = 24, b = 30. Тогда НОД (24, 30) = 6. Если а = 10, b = 33, то НОД (10, 33) = 1; НОД (а, а) = а. Пусть а = 12, b = 48. Тогда НОД (12, 48) = 12.

Теорема 9. Пусть а и b натуральные числа, Теорема 9. Пусть а и b натуральные числа, Тогда НОД (а,b)= где γi = min (αi,βi), i = 1,2,3, …, n.

Следствие 10. Следствие 10. Любой общий делитель чисел а и b является также делителем НОД (а, b). Определение 11. Число а называется кратным числу b (а,b N), если а делится на b или, что тоже самое, b есть делитель а. Тот факт, что а делится на b, будет обозначать как b .

Пример. Пусть b =3. Пример. Пусть b =3. Тогда кратным ему будут числа 3,6, 9, 12, … . Их можно описать общей формулой а = 3n (n N). Этот пример показывает, что в отличие от делителей, количество кратных любому натуральному числу b бесконечно.

Определение 12. Определение 12. Если число а делится на число b и с, то а называется общим кратным чисел b и с. Примеры. Если b = 6, c = 8, то общее кратное этих чисел равно 24. Также общими кратными являются числа 48, 72, … .

Теорема 13. Пусть, Теорема 13. Пусть, Тогда число является общим кратным чисел b и с тогда и только тогда, когда α1 ≥ max (β1,γ1), α2 ≥ max (β2,γ2), …, αn ≥ max (βn,γn).

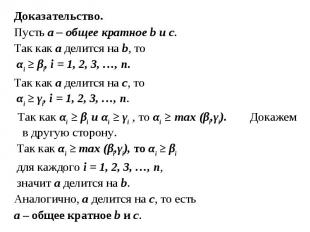
Доказательство. Доказательство. Пусть а – общее кратное b и с. Так как а делится на b, то αi ≥ βi, i = 1, 2, 3, …, n. Так как а делится на с, то αi ≥ γi, i = 1, 2, 3, …, n. Так как αi ≥ βi и αi ≥ γi , то αi ≥ max (βi,γi). Докажем в другую сторону. Так как αi ≥ max (βi,γi), то αi ≥ βi для каждого i = 1, 2, 3, …, n, значит а делится на b. Аналогично, а делится на с, то есть а – общее кратное b и с.

Определение 14. Определение 14. Самое маленькое из всех общих кратных натуральных чисел b и с называется наименьшим общим кратным b и с и обозначается НОК (b, c). Примеры. НОК (3, 5) = 15, НОК (4, 6) = 12, НОК (36, 64) = 576, НОК (2, 8) = 8, НОК (а, а) = а, НОК (1, а) = а.

Теорема 15. Пусть Теорема 15. Пусть Число является НОК (b, с) в том и только в том случае, когда αi = max (βi,γi), i = 1, 2, 3, …, n

Следствие 16. Следствие 16. Любое общее кратное чисел b и с делится на НОК(b, с). Лемма 17. Для любых чисел х, у max (x, y) + min (x, y) = x + y.

Доказательство. Рассмотрим три случая: Доказательство. Рассмотрим три случая: 1)       х = у, тогда max (x, y) = x, min (x, y) = x, поэтому max (x, y) + min (x, y) = 2 x и х + у = 2х ; 2)       х > у, тогда max (x, y) = x, min (x, y) = y, следовательно max (x, y) + min (x, y) = x + y ; 3)       x < y, тогда max (x, y) = y, min (x, y) = x, поэтому max (x, y)+ min (x, y) = y + x = x + y.

Теорема 18. Теорема 18. Для любых натуральных чисел b и с НОД (b, с) · НОК (b, с) = b · c. Доказательство. Пусть и Тогда

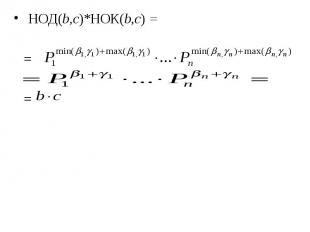
НОД(b,c)*НОК(b,c) = НОД(b,c)*НОК(b,c) = = =

Определение 19. Числа а и b называются взаимно простыми, если НОД (а, b) = 1. Другими словами, если а и b не имеют общих делителей, отличных от 1. Определение 19. Числа а и b называются взаимно простыми, если НОД (а, b) = 1. Другими словами, если а и b не имеют общих делителей, отличных от 1. Примеры. 3, 8 – взаимно просты, 1, 5 взаимно просты, 4, 6 – не взаимно просты.

Определение 20. Определение 20. Функцией Эйлера φ (n) называется количество чисел меньших, либо равных n, которые взаимно просты с n. Примеры. 1) φ (12) = 4. Перечислим все числа ≤ 12 и взаимно простые с 12: 1,5, 7, 11; 2) φ(36) = 12. Перечислим все необходимые числа: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35; 3) φ(7) = 6.

Теорема 21. Теорема 21. Пусть n = , причем αi > 0 и ki kj (i j), i ,j= 1, 2, …, n. Тогда

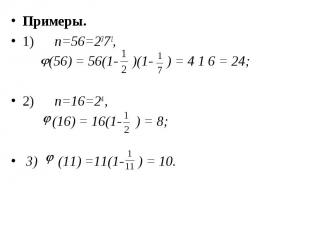
Примеры. Примеры. 1)      n=56=2371, (56) = 56(1- )(1- ) = 4 1 6 = 24; 2)      n=16=24 , (16) = 16(1- ) = 8; 3) (11) =11(1- ) = 10.