Презентация на тему: Развитие логического мышления на уроках математики

* Развитие логического мышления на уроках математики. Сделать учебную работу насколько возможно интересной для ребёнка и не превратить этой работы в забаву – это одна из труднейших и важнейших задач дидактики. Выполнила : учитель математики и информатики Ушанкова А.С.

* Приёмы логической мыслительной деятельности: Необычный подход к рассмотрению вопроса; Поиск ассоциации; Перенос идеи из другой области знаний; «Игра» с объектами и идеями.

* Приёмы развития логического мышления. Дидактические игры; Математические головоломки; Числовые ребусы; Геометрия в пространстве; Задачи- шутки; Включение в урок математических героев.

* Дидактические игры. В игре всегда содержится элемент неожиданности и необычности, решается какая-либо задача, проблема, т. е. игра выполняет на уроке те же функции, что и занимательная задача. Очень часто здесь присутствует соревновательный элемент и возможности для создания игровых ситуаций чрезвычайно велики.

* Игра в – 66. Играют двое. Первый записывает любое целое отрицательное число, большее -10, второй, устно прибавив к нему целое отрицательное число, большее -10, записывает сумму, первый к этой сумме устно прибавляет целое отрицательное число, большее -10, и записывает сумму и т. д. Побеждает тот, кто запишет число -66.

* Математические головоломки. Основное достоинство подобных заданий- они требуют от ученика выделения существенных связей между компонентами заданий, при этом часто происходит смена хода мысли учеников на обратный, что увеличивает свободу действий ученика, которая в обычных условиях достигается очень редко.

* Математические головоломки. Вырежьте 16 одинаковых квадратов 4-х цветов – по 4 квадрата каждого цвета. На 4-х квадратах каждого цвета напишите цифры 1, 2, 3, 4. Сложите теперь квадрат так, чтобы одинаковые цифры и одинаковые цвета не повторялись ни в строках, ни в столбцах, ни на диагоналях квадрата.

* Числовые ребусы. В этом логическом приёме используются зашифрованные задания, требующие рассуждений, обратных тем, к которым привыкли ученики. Фактически числовые ребусы есть ни что иное, как клубок логических связей, который надо распутать.

* Русский язык + математика = логика. один вагон деталь + один + вагон + деталь --------- ---------- ------------ много состав изделие Вместо одинаковых букв надо вставить одинаковые цифры так, чтобы получилось верное равенство.

* Геометрия в пространстве. Геометрия в целом, как и её основные составляющие- фигуры, логика и практическая применимость- позволяют учителю гармонично развивать образное и логическое мышление ребёнка любого возраста, прививать ему навыки практической деятельности.

Стереозрение

* Задачи – шутки. На первый взгляд эти задачи очень простые, но нельзя спешить быстро дать ответ- он может оказаться неверным. Правильное решение таких задач чаще всего не требует никаких дополнительных знаний,- главное внимательно читать условие задачи и постараться миновать расставленные ловушки.

* Математик, который не является поэтом, никогда не достигнет совершенства в математике. Тигр старше дикобраза в два с половиной раза, По сведениям удода тому назад три года В семь раз он старше был, Чем дикобраз. Учтите всё и взвесьте: Сколько же им вместе?- Позвольте мне спросить у вас.

* Включение в урок математических героев. В урок вводится какой-либо математический герой, который или решает задание, или предлагает его для решения, или придумывает фокусы и т. д. Иногда вводятся два героя: один сообразительный, а другой невнимательный.

* Творческим считается любое действие, которое эффективно и вызывает удивление. Сказка- это поэзия. Казалось бы сказка и математика- понятия не совместимые. Яркий сказочный образ и сухая абстрактная мысль! Но часто решать такие задачи очень увлекательно, хочется помочь попавшему в беду любимому герою. Красота решения, неожиданный поворот мысли, логика рассуждений- всё это усиливает интерес к этим задачам.

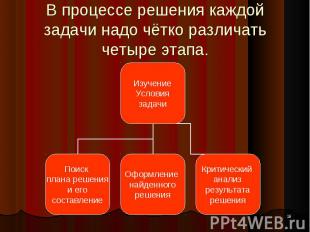
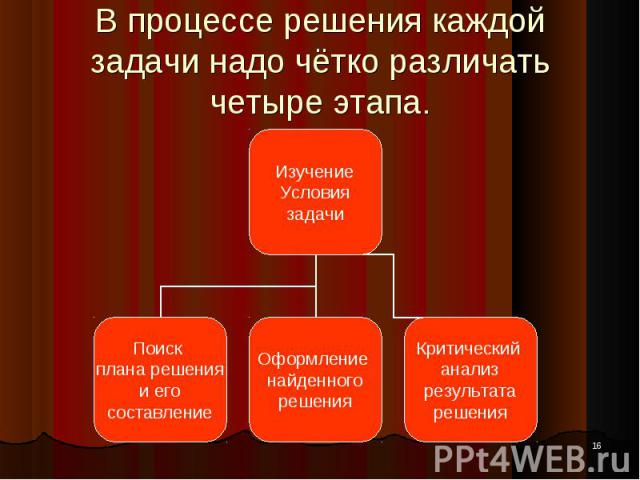
* В процессе решения каждой задачи надо чётко различать четыре этапа. Изучение Условия задачи Поиск плана решения и его составление Оформление найденного решения Критический анализ результата решения