Презентация на тему: Развитие логического мышления младших школьников на уроках математики

Развитие логического мышления младших школьников на уроках математики

На современном этапе развития общества наша страна находится в сложной ситуации, переживает трудные времена. Общество стоит на пороге новой идеологии, нового строя и новой политики. Меняется жизнь: претерпевают изменения её социальная и нравственная сферы. В связи с этим возникает много проблем, какая должна быть экономика, политика, как обеспечить достойный уровень жизни всех граждан государства. Общество не может стоять на месте, оно развивается, и для прогресса нужны люди свободные, высокообразованные, творческие, обладающие высоким уровнем развития разных видов мышления.

Одним из важнейших условий построения обучения, которое способствует развитию мыслительной деятельности школьников на уроках математики, является пробуждение их к самостоятельной мысли. Развитие у школьников теоретического сознания и мышления есть следствие того, что соответствующими знаниями, умениями и навыками учащиеся овладевают в форме учебной деятельности. Это овладение теоретическими знаниями происходит в диалоге, дискуссии, в их сознании постоянно функционирует анализ, обобщение, планирование, рефлексия.

Изменение приоритетных направлений развития современной системы образования ставит перед школой задачу формирования творческой личности, способной ориентироваться в многообразии окружающего мира. Это обусловлено качественными изменениями социального заказа общества, потребностями в творчески мыслящих людях, обладающих нестандартным взглядом на проблемы. Одной из составляющих этой проблемы является задача развития гибкости мышления учащихся.

В настоящее время в психологии существует два подхода к пониманию гибкости мышления (П. Торренс, Дж.Гилфорд) гибкость рассматривается как показатель креативности, характеризующей возможности и способности человека, которые прямо и непосредственно связаны с его способностью к обучению; стимулом их проявления является не столько многообразие имеющегося знания сколько восприимчивость к новым идеям, ломающим устоявшиеся стереотипы. Показатель гибкости, согласно данному подходу, оценивает способность выдвигать разнообразные идеи, переходить от одного аспекта к другому, использовать разнообразные стратегии проблем.

Я работаю по методической теме «Развитие логического мышления младших школьников на уроках математики». Тема является сферой моего методического интереса. Целью работы по данной теме является попытка решить проблемы активизации познавательной деятельности учащихся, воспитания у детей самостоятельности и активности как черт личности, формирование стремления и привычки к трудовому усилию, настойчивости в преодолении трудностей. Одной из важнейших задач, ставлю развитие логики мышления, которая бы позволила детям строить умозаключения, приводить доказательства, высказывания, логически связанные между собой; делать вывод, обосновывая свои суждения, и, в конечном счёте, самостоятельно приобретать знания.

С древнейших времён педагоги ищут способы наилучшего обучения детей. Ставятся задачи определить такие методы технологии, чтобы оно протекало быстро и качественно, с разумными затратами сил учителей и учеников. Испробовано уже многое. Не осталось ни одного более или менее очевидного пути, по которому бы не пытались идти учителя. Известно, что новообразованием младшего школьного возраста выступает логическое мышление. От того, насколько сформированы его элементы у ребёнка, поступающего в школу, будет во многом зависеть успешность обучения в школе, и математики в частности. Учёными указывается, что большое значение в развитии логического мышления детей имеет развитие мыслительных операций.

Важнейшей задачей математического образования является вооружение учащихся общими приёмами мышления, развитие способности понимать смысл поставленной задачи, умение логически рассуждать. Каждому важно научиться анализировать, отличать гипотезу от факта, отчётливо выражать свои мысли. Большие развивающие возможности в этом плане имеют уроки математики. В современной ситуации обучения математике ставятся задачи, связанные не только вооружением младших школьников математическими знаниями, умениями и навыками, но и развитием познавательных способностей на математическом материале. Большое внимание решению последней задачи уделяют развивающие программы математического образования.

Математика проникает почти во все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения. В качестве развития познавательных процессов при этом используются различные методы и средства. Наиболее эффективным средством развития логического мышления младших школьников выступает игра. Наилучшим образом используются логико-математические игры, в которых смоделированы математические отношения, закономерности, предполагающие выполнение логических операций.

В.А. Сухомлинский писал: «…Не обрушивайте на ребёнка лавину знаний… под лавиной знаний могут быть погребены пытливость и любознательность. Умейте открыть перед ребёнком в окружающем мире что-то одно, но открыть так, чтобы кусочек жизни заиграл перед детьми всеми цветами радуги. Открывайте всегда что-то неизведанное, чтобы хотелось ещё и ещё раз возвратиться к тому, что он узнал». Поэтому обучение, воспитание и развитие ребёнка должны быть непринужденными, осуществляться через свойственные конкретному возрасту виды деятельности и педагогические средства. Таким развивающим средством выступает игра.

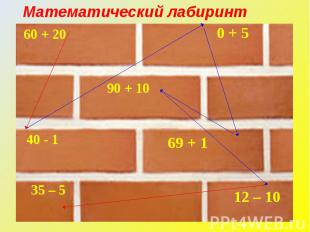
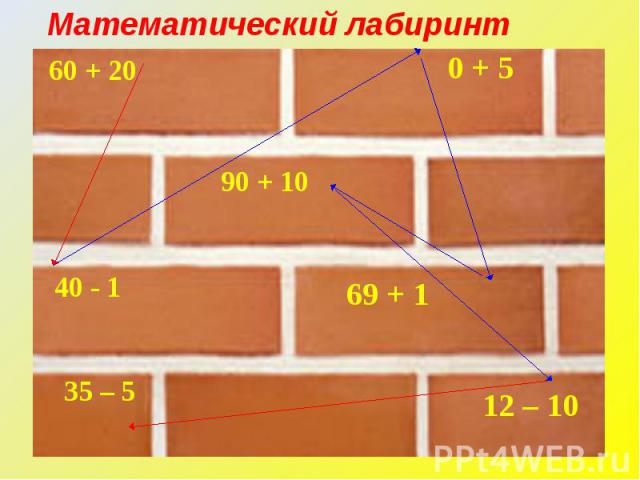
Математический лабиринт

Половим рыбку?

В данной игре присутствует и любимый мультфильм детей, и предметы с изображением рыбок(бумажных), на которых написано задание, это для них интересно и увлекательно, и к тому же задания можно заготавливать самые разнообразные, в частности, развивающие логику.

Разгадывание различных кроссвордов, шарад…

Развитие мышления и речи решается также в непрерывной связи. При общении детей в игре речь активизируется, развивается способность аргументировать свои утверждения, доводы. Играя, ребёнок может не только закрепить ранее полученные знания, но и приобретать новые навыки, умения, развивать умственные способности. В этих целях используются специальные на умственное развитие ребёнка игры, насыщенные логическим содержанием. В сюжетно-ролевой, творческой играх отражаются впечатления детей об окружающем мире, понимании происходящих событий и явлений. В огромном количестве игр с правилами запечатлены разнообразные знания, умственные операции, действия, которые дети должны освоить. Освоение это идёт по мере общего умственного развития, вместе с тем в игре это развитие и осуществляется. С помощью дидактической игры детей приучают самостоятельно мыслить, использовать полученные знания в различных условиях в соответствии с поставленной задачей. Многие игры ставят перед детьми задачу рационального использования имеющихся знаний в мыслительных операциях:Находить характерные признаки предметах и явлениях окружающего мира;Сравнивать, группировать, классифицировать предметы по определённым признакам, делать правильные выводы.

Можно, например применять задания такого вида:- Что общего у этих предметов? (цветы)- Сгруппируйте их.- Каким способом вы это сделаете? (название цветов, цвет)Дети распределяют цветы по группам, и вот что получается:

Далее задаются вопросы по сравнению этих предметов, например:- Сколько рядов у вас получилось?- Как называются цветы в первом ряду?- Какого они цвета?Сколько их?-Во втором ряду столько же?- Как называются цветы во втором ряду? (и т.д.)

Ещё пример группировки предметов, в данном случае предметы уже в группах, учителем задаются вопросы такого характера:- Как называются фигуры, которые вы видите?- Сколько рядов? - Найдите и назовите сходство и различие этих фигур?- Где можно применить в окружающей жизни эти кубики?

Специальная педагогическая работа по развитию логического мышления младших школьников даёт положительный результат, повышая в целом уровень их способностей к обучению в дальнейшем. В более старшем возрасте никаких принципиально новых интеллектуальных операций в системе мыслительной деятельности человека не происходит. Имеется ряд педагогических исследований (Ш.А. Амонашвили, А.В Белошистая, В.В. Давыдов, Г. Доман, Н.Б. Истомина, М. Монтессори, И.Л. Никольская и др.), доказывающих, что при организации систематического педагогического воздействия на развитие логического мышления соответствующие интеллектуальные операции могут быть сформированы у ребёнка в младшем школьном возрасте. Становление и активизация «сильного мышления» у ребёнка интеллектуализирует его познавательную деятельность, делает её активно-поисковой, формирует творческое и деятельностное отношение к действительности. Ребёнок чувствует себя уверенно в различных отношениях с окружающим миром.

Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. Выдающийся отечественный математик А.Н. Колмогоров писал: «Математика не просто один из языков. Математика – это язык плюс рассуждения, это как бы язык и логика вместе. Математика – орудие размышления. В ней сконцентрированы результаты точного мышления многих людей. При помощи математики можно связать одно рассуждение за другим, очевидные сложности природы с её странными законами и правилами, каждое из которых допускает отдельное очень подробное объяснение, на самом деле тесно связаны. Таким образом, математика позволяет сформировать определённые формы мышления, необходимые для изучения окружающего нас мира.

Мышление человека, и в частности школьника, наиболее ярко проявляется при решении задач. Любая мыслительная деятельность начинается с вопроса, который ставит перед собой человек, не имея готового ответа на него. Иногда этот вопрос ставят другие люди, но не всегда акт мышления начинается с формулировки вопроса, на который надо ответить, задачи, которую надо решить, с сознания чего-то неизвестного, что надо понять и уяснить. Человек может мыслить с разной степенью обобщённости, в большей или меньшей степени, опираться в процессе мышления на восприятие, представления или понятия. В устном счёте можно предлагать задачи простые на смекалку и на развитие логического мышления. Вычисления в этих задачах должны быть нетрудоёмкими, чтобы не отнимали много времени на уроке, но заставляли думать. При этом развиваются такие приёмы логического мышления, как синтез, аналогия, сравнение, классификация, обобщении, необходимые для интеллектуального роста каждого ребёнка.

Из-под ворот видно 8 кошачьих лап. Сколько кошек во дворе?2. Горело 7 лампочек, 3 из них погасли. Сколько лампочек осталось?Обведи правильный ответ:7, 3, 4, 03. Что тяжелее: 1кг ваты, или 1кг железа?Вата, железо, поровну

Сравнение – это сопоставление предметов и явлений с целью найти сходство и различие между ними.Анализ – это мысленное расчленение предмета или явления на образующие его части, выделение в нём отдельных частей, признаков и свойств.Синтез – это мысленное соединение отдельных элементов, частей и признаков в единое целое. Анализ и синтез неразрывно связаны, находятся в единстве друг с другом в процессе познания. Анализ и синтез – важнейшие мыслительные операции.Абстракция – это мысленное выделение существенных свойств и признаков предметов или явлений при одновременном отвлечении от несуществующих. Абстракция лежит в основе обобщения.Обобщение – мысленное объединение предметов и явлений в группы по тем общим и существенным признакам, которые выделяются в процессе абстрагирования. Процессам абстрагирования и обобщения противоположен вопрос конкретизации.Конкретизация – мыслительный переход от общего к единичному, которое соответствует этому общему. В учебной деятельности конкретизировать – значит привести пример.

В новых образовательных стандартах сказано: «при обучении различным предметам используются задачи, которые принято называть учебными, с их помощью формируются предметные знания, умения, навыки. Особенно широко применяются задачи в математике, физике, химии, географии. Как правило, в них используются математические способы решения». В связи с этим основная работа для развития логического мышления на уроках математики должна вестись с задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления. Нестандартные логические задачи – это инструмент для такого развития.

В любой творческой деятельности, в учёбе, в труде, в игре, да и просто в жизни – везде внимание, смышлёность, умение логически мыслить – необходимы человеку, они помогают решать проблемы, находить выход из сложных ситуаций и полезны для здоровья: поддерживают тонус головного мозга, смекалку можно развить, упражняясь в решении занимательных задач, головоломок, разбирая математические игры, шутки и фокусы, то есть любые задания, требующие работы ума.

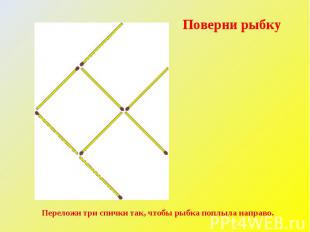
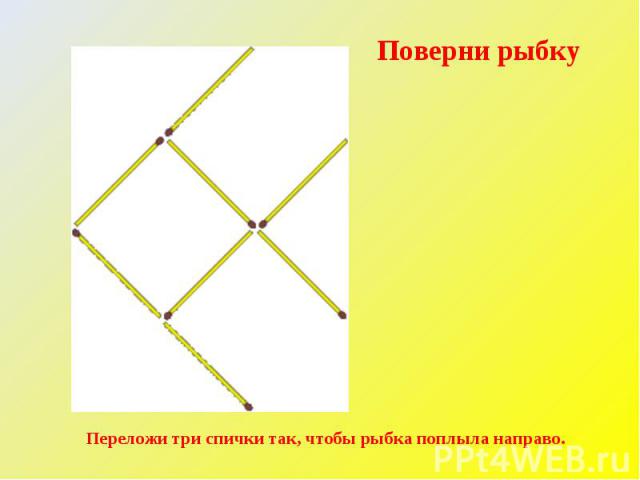
Поверни рыбку Переложи три спички так, чтобы рыбка поплыла направо.

ответ

Систематическое использование на уроках математики специальных задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни. Анализ литературы по проблеме развития логического мышления младших школьников на уроках математики позволяет сделать вывод о том, что в начальной школе именно этот предмет является основой развития у учащихся познавательных действий, в первую очередь логических.

Исходя из выше изложенного, при обучении необходимо найти в педагогическом процессе такие условия, которые могли бы в максимальной степени способствовать проявлению самостоятельности и активности мышления учащихся, а также продвижению их в умственном развитии. Важнейшей задачей математического образования является вооружение учащихся общими приёмами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоить навыки алгоритмического мышления. Каждому важно научиться анализировать, отличать гипотезу от факта, отчётливо выражать свои мысли, а с другой стороны развить мысли и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения). Именно математика предоставляет благоприятные возможности для решения этих задач.