Презентация на тему: Разложение многочлена на множители

Через занимательность проникает в сознание ученика сначала ощущение прекрасного, а затем, при последующем систематическом изучении математики, и понимание красоты ее методов. Б.А.Кордемский. Разложение многочлена на множители. Разработка презентации выполнена Кунжаровой Ю.О.ГОУ СОШ №303 г. С-Петербург

Урок1. Вынесение общего множителя за скобки. Представление многочлена в виде произведения двух или нескольких многочленов называют разложением многочлена на множители.6a2b+15b2= 3b2a2+ 3b5b= 3b(2a2+5b)Данный способ разложения многочлена на множители называют вынесением общего множителя за скобки.

Рассмотрим примеры разложения многочлена на множители. –15x2y3–30x3y2+45x4y= –15x2y1(y2+2xy–3x2) –15x2y3–30x3y2+45x4y=15x2y1(–y2–2xy+3x2) 3a3–15a2b+5ab2=a(3a2–5ab+5b2) 8a4b–12a2b4+16a3b2=4a2b(2a2–3b3+4ab) c3+c4+c5=c3(1+c+c2)

Решаем сами. Закончите разложение: 5ax–30ay=5a (………..) 3x2+6x=3x (…………) a2b–ab2= ab(………..) 5a2+25a4=5a2 (……….) 12с3b2–18c2b2=6c2b2 (………..) 9xm5+3x2m4–6xm2=3xm2 (………..)

Если все члены многочлена содержат общий множитель, то этот множитель можно вынести за скобки. Чтобы разложить многочлен на множители вынесением общего множителя за скобки, надо: Найти общий множитель.Вынести его за скобки.

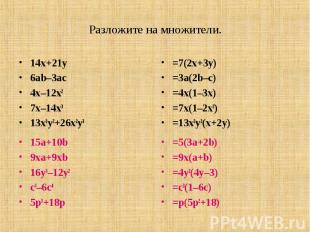
Разложите на множители. 14x+21y6ab–3ac4x–12x27x–14x313x3y2+26x2y3=7(2x+3y)= 3a(2b–c)=4x(1–3x)=7x(1–2x2)= 13x2y2(x+2y)15a+10b9xa+9xb16y3–12y2c3–6c45p3+18p=5(3a+2b)= 9x(a+b)= 4y2(4y–3)=c3(1–6c)=p(5p2+18)

* Докажите, что значение выражения: 165+164 кратно 17 Решение:165+164=*Докажите, что 78–77+76 делится на 43.Решение: 78–77+76=76 (72–7+1)=76∙(49–7+1)==(76∙43):43, т.к.43:43