Презентация на тему: Разложение многочлена на множители с помощью формул сокращенного умножения

Алгебра 7 класс УМК А.Г.Мордкович Учитель Доценко Людмила Павловна МОУ «ООШ с.Приозерное»

Разложение многочлена на множители с помощью формул сокращенного умножения Цель: формирование умений применять формулы сокращенного умножения при разложении многочлена на множители.

Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. Русский математик,  кораблестроитель, академик  Алексей Николаевич  Крылов

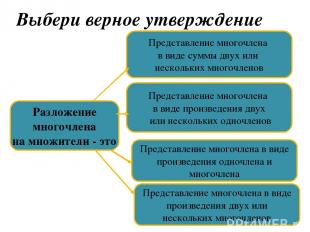
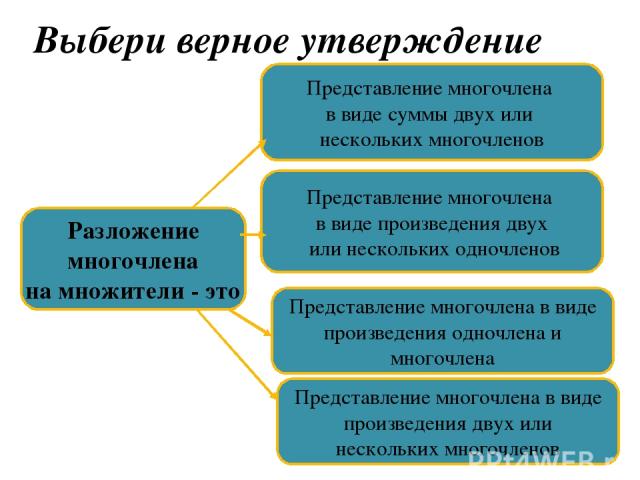
Выбери верное утверждение Разложение многочлена на множители - это Представление многочлена в виде суммы двух или нескольких многочленов Представление многочлена в виде произведения двух или нескольких одночленов Представление многочлена в виде произведения двух или нескольких многочленов Представление многочлена в виде произведения одночлена и многочлена

Устный счет 1)Представить одночлен в виде квадрата одночлена: 16x2; 81a4b6; 36m2n8; 121 x2y2. 2) Представить одночлен в виде куба одночлена: 27m3n3; 8a6b9; 125x3y6; 64p6g12. 3)Представить в виде удвоенного произведения: 50xy; 32a5b; 78cd; 56z3k7.

4)Разложить многочлен на множители 8x -12y x3 – 3x2- x a4 + a2b 9p4+ 18p2- 27p 5)Представьте выражение в виде квадрата двучлена a2 – 2ab + b2 a2- 12a + 36 81+18y + y2

Устный счет Разложить многочлен на множители: 8x –12y a4 + a2b x3- 3x2- 3x 9p4+ 36p2- 27p Представить в виде квадрата двучлена: a2- 2ab + b2 a2- 12ab +36 81- 18y + y2 = 4(2x -3у) = a2(a2+b) = x(x2- 3x -1) = 9p (p3+4p -3) = (a –b)2 = (a – 6) = (9 + y)2

Разложение многочлена на множители с помощью формул сокращенного умножения

Алгоритм разложения разности квадратов на множители: 1.Представить двучлен в виде разности квадратов. 2.Выполнить разложение по формуле а2-в2= (а-в)(а+в) разность квадратов Пример: 169 – m2=( 13)2-m2= (13+ m)(13- m)

Алгоритм разложения трехчлена на множители: 1.Убедимся, что трехчлен является полным квадратом и содержит сумму квадратов одночленов, а также удвоенное произведение этих одночленов. 2.Выполнить разложение по формуле ( a + b)2 = a2 + 2ab + b2 - квадрат суммы Пример: a2 + 4ab +4b2= a2+ (2b)2 +2*2ab = =(a + 2b)2

Алгоритм разложения трехчлена на множители: 1.Убедимся, что трехчлен является полным квадратом и содержит сумму квадратов одночленов , а также удвоенное произведение этих одночленов. 2.Выполнить разложение по формуле  (a - b)2 = a2 - 2ab + b2 - квадрат разности Пример: 4x4- 12xy + 9y6= (2x2)2+ (3y3)2- 2*2x2 *3y3= (2x2- 3y3)2 квадрат разности

Алгоритм разложения cуммы кубов на множители: 1.Представить двучлен в виде суммы кубов. 2.Выполнить разложение по формуле а3+в3= (а + в)(а2 - aв + b2) сумма кубов Пример: 27 + m3= (3)3+ m3=(3 + m) ((3)2 – 3*m+ m2) = (3 + m)(9- 3m +m2)

Алгоритм разложения разности кубов на множители: 1.Представить двучлен в виде разности кубов. 2.Выполнить разложение по формуле а3-в3= (а- в)(а2+ aв + b2) разность кубов Пример: 64а6- 8b9=(4a2)3 - (2b3)3 =(4a2 – 2b3)((4a2)2+ 4a2*2b3 +(2b3)2)=(4a2- 2b3)(16a4+ 8a2b3+4b6 )

Проверь себя! №33.16(а,б) №33.18(а,б) №33.22(а,б) №33.23(а,б)

Смотри не ошибись! I вариант x2- 81 m2-20m +100 25x2+40x+16 64a3- 27d3 II вариант x2- 25 x2-16x +64 49x2+56x+16 8a3+ 216d3

Проверка I вариант (x -9)(x+9) (m-10)2 (5x +4)2 (4a – 3d)(16a2+ 12ad +9d2) II вариант (x-5)(x+5) (x -8)2 (7x +4)2 (2a + 6d)(4a2-12ad +36d2)

Домашнее задание §33, №33.16(в,г) №33.18(в,г) №33.22(в,г) №33.23(в,г)

Я сегодня узнал… Предлагаю выразить своё отношение к полученной информации с помощью стратегии «Чемодан» -«Чемодан» - если открытая на уроке информация нужная и будет использоваться на практике - «Мясорубка», если полученная информация, недостаточно осознанна или требует дальнейшего осмысления, использование на практике предполагается - «Корзинка», если информация полученная на уроке, является не нужной или уже знакомой

Продолжи предложения: Я сегодня узнал…

Спасибо за урок!