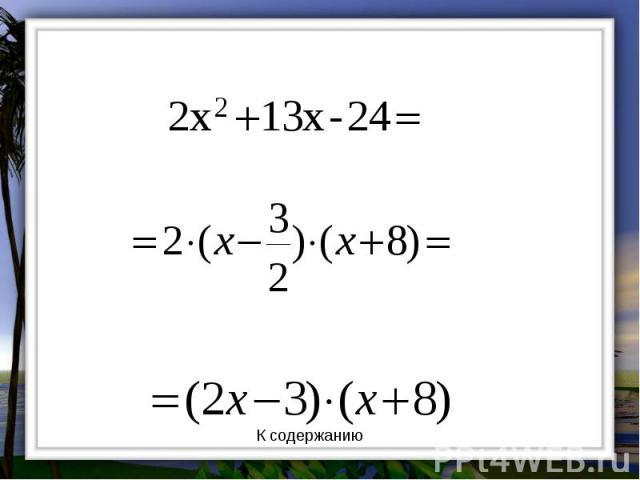Презентация на тему: Разложение многочлена на множители с помощью комбинации различных приемов

Разложение многочлена на множители с помощью комбинации различных приемов 7 класс
Содержание Формулы сокращенного умножения

Формулы сокращенного умножения

1. Квадрат суммы

2. Квадрат разности

3. Разность квадратов

4. Куб суммы

5. Куб разности

6. Сумма кубов

7. Разность кубов

Вынесение общего множителя за скобки Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен.

Алгоритм нахождения общего множителя нескольких одночленов Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов). Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени. Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.

Пример Разложить на множители: x4y3 - 2x3y2 + 5x2. Воспользуемся сформулированным алгоритмом. Наибольший общий делитель коэффициентов –1, -2 и 5 равен 1. Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2. Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки. Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим: -x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5).

Способ группировки

Алгоритм разложения многочлена на множители способом группировки:

Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен
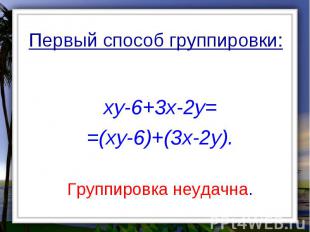
Первый способ группировки: xy-6+3x-2y= =(xy-6)+(3x-2y). Группировка неудачна.

Второй способ группировки

Третий способ группировки:


Разложение квадратного трехчлена на множители
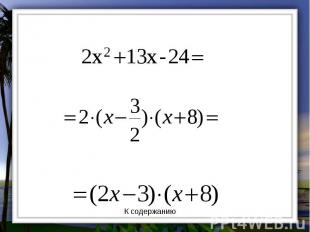

Спасибо за внимание! Спасибо за внимание!