Презентация на тему: Разложение многочлена на множители с помощью комбинации различных приемов

Разложение многочлена на множители с помощью комбинации различных приемов Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький.Конфуций

Рейтинговая карта

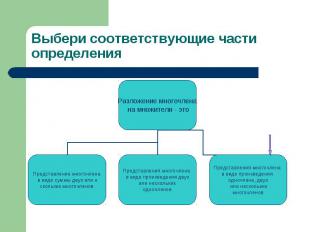
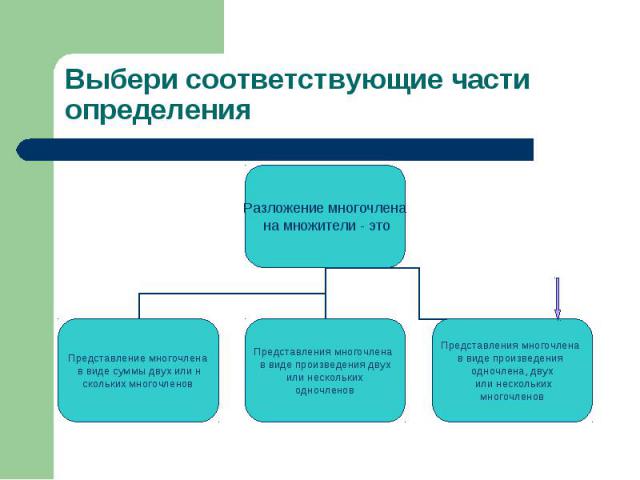
Выбери соответствующие части определения

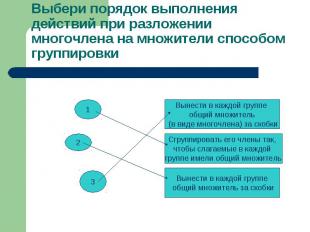
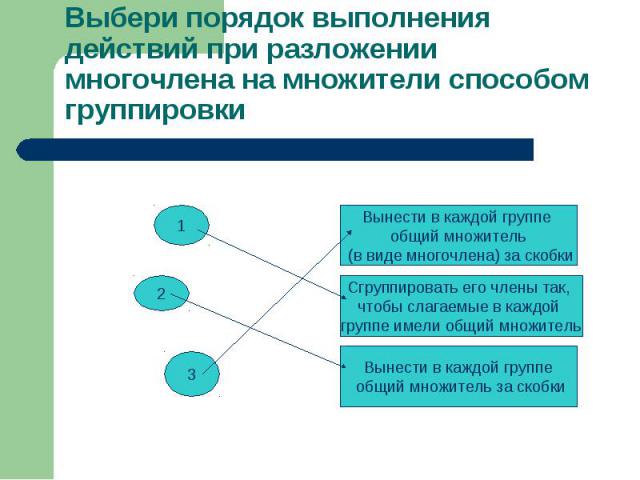
Выбери порядок выполнения действий при разложении многочлена на множители способом группировки

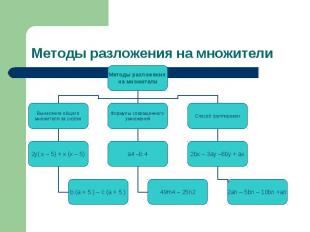
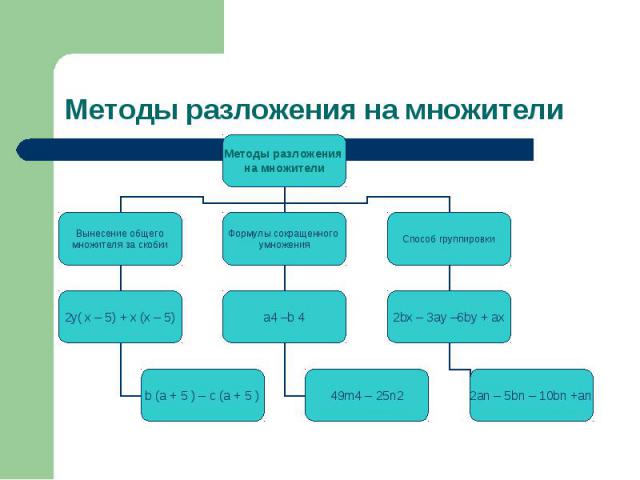
Методы разложения на множители

4. Отметить знаком «+» верные выражения

Методы разложения на множители.

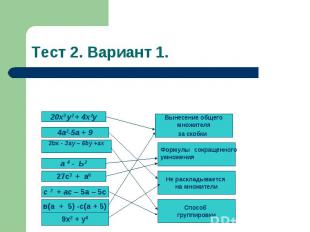
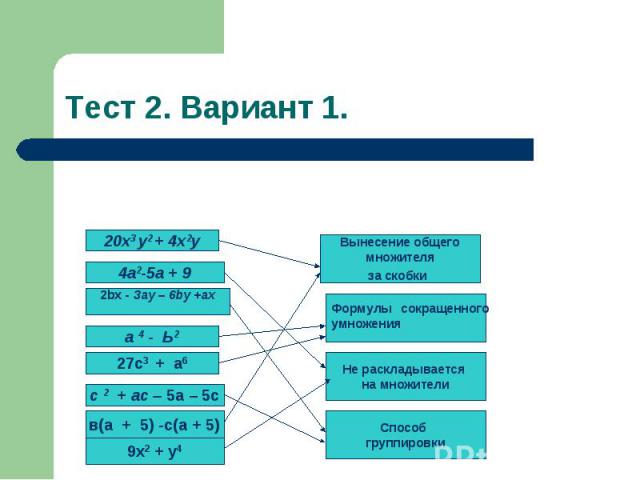
Тест 2. Вариант 1.

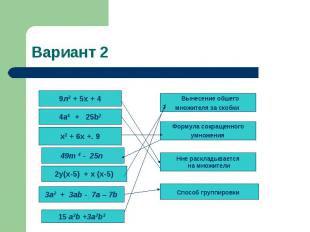
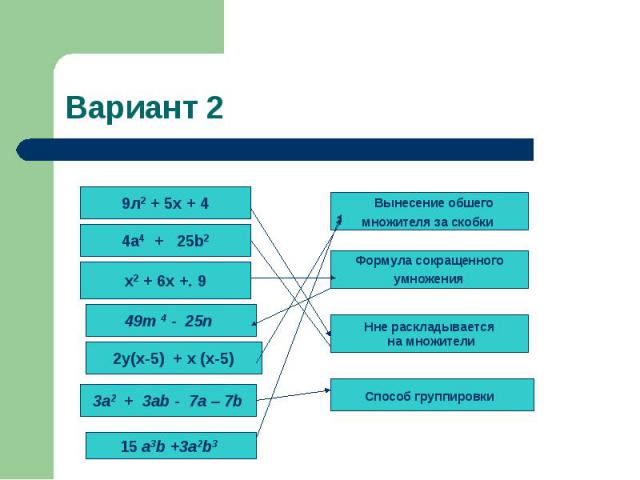
Вариант 2

Вынесение общего множителя Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые.Таким общим множителем может быть не только одночлен, но и многочлен.

Группировка Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.

Применение формул сокращенного умножения Здесь группа из двух, трех (или более) слагаемых, которая обращает выражение, входящее в одну из формул сокращенного умножения, заменяется произведением многочленов.

Ответы: 1. 3 (а+ 4b)2.  (2 + а)(а + b)3.  (За-4b) (За+ 4b )4.  7аb (а-2b +1 )5.  (m-q )(m+ n –1 )6.  (2а- b)27. (2а + с) (За + 2b ) 8. (5а + 7b )2 1. (4а + b)2 . 2. (3 +n ) (m-n ) 3. 5 ( а –5b ) 4. (а- q)(а-3b+1) 5. (3а-5b)2 6. (2a + 3b)(а + 2с) 7. (12а-5b) (12а+ 5b) 8. 9аb ( а2-2b-1 )

Преобразование цепых выражений 1. Вынести общий множитель за скобку (если он есть).2.     Попробовать разложить многочлен на множители по формулам сокращенного умножения.3.     Попытаться применить способ группировки (если предыдущие способы не привели к цели).

Задание 1. Решить уравнение : x2 - 15x + 56 = 0

Задание № 2 ( 3n - 4 )2 - n2  Задание № 2 ( 3n - 4 )2 - n2   Решение : (3n- 4)2 -n2 = (3n - 4 - n )( 3n - 4 + n ) =( 2n - 4) (4n - 4) = 8 (n - 2 ) (n - 1 )

Пример 4. n3 + Зn2 + 2n.   Решение. n3 + Зn2 + 2n = n (n2 + Зn + 2) = n (n2 + 2n + n + 2) = n ((n2 + 2n) + (n + 2)) = n (n (n + 2) + n + 2) = n (n + 1) (n + 2). Комбинировали три приема:-   вынесение общего множителя за скобки;-   предварительное преобразование;-   группировку.Отмечаем, что для решения этого примера мы использовали еще один прием разложения на множители - предварительное преобразование.

Разложить на множители, используя различные способы. Ответы