Презентация на тему: Разложение многочлена на множители

Разложение многочлена на множители с помощью комбинации различных приемов Урок алгебры в 7 классе. МОУ «Побединская СОШ», учитель математики Трубачева Светлана Владимировна. 900igr.net

Разложение многочлена на множители с помощью комбинации различных приемов. Три пути ведут к познанию: путь размышления – это путь самый благородный, путь подражания – этот путь самый легкий и путь опыта – этот путь самый горький. Конфуций

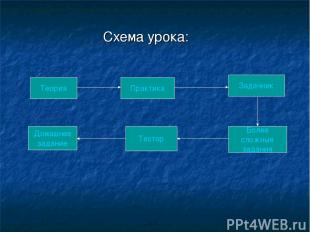
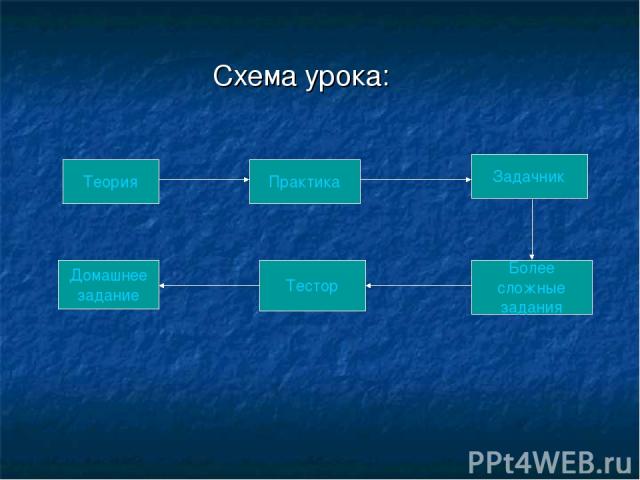
Схема урока: Теория Более сложные задания Тестор Задачник Домашнее задание Практика

Теория Разложение многочлена на множители – это представление многочлена в виде произведения двух или нескольких многочленов Комбинировали три приема: Вынесение общего множителя за скобки С помощью формул сокращенного умножения Способ группировки Схема урока

Провести классификацию данных многочленов по способу разложения на множители. Метод разложения на множители Формулы сокращенного умножения Способ группировки 20х3у2 + 4х2у 15а3b + 3а2b3 а4 –b8 а2 + аb – 5а - 5b 2bх – 3ау - 6bу + ах 2ап - 5bm - 10bп + аm 27b3 +а6 3а2 + 3аb – 7а - 7b Х2 + 6х + 9 49m4 – 25п2 b(а +5) – с(а + 5) 2у(х – 5) + х(х – 5) Вынесение общего множителя за скобки ответы Схема урока

Провести классификацию данных многочленов по способу разложения на множители. 20х3у2 +4х2у а4 – b8 2bх -3ау -6bу + ах b(а +5) - с(а +5) 27b3 + а6 а2 + аb – 5а -5b 15а3b +3а2b3 х2 + 6х + 9 2аn -5bm -10bn + аm 2у(х – 5) +х(х – 5) 49m4 - 25n2 3а2 +3аb -7а -7b За каждый, верно записанный многочлен, 1 балл. Формулы сокращенного умножения Способ группировки Метод разложения на множители Вынесение общего множителя за скобки теория

Вынесение общего множителя за скобки Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен. теория

Применение формул сокращенного умножения Здесь группа из двух, трех (или более) слагаемых, которая обращает выражение, входящее в одну из формул сокращенного умножения, заменяется произведением многочленов. а2 + 2аb + b2 = (а + b)2 а2 - 2аb + b2 = (а - b)2 а2 - b2 = (а – b)(а + b) а3 + b3 = (а + b)(а2 - аb + b2) а3 - b3 = (а - b)(а2 + аb + b2) теория

Способ группировки Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом. Чтобы разложить многочлен на множители способом группировки, нужно: Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынести в каждой группе общий множитель в виде одночлена за скобки Вынести в каждой группе общий множитель (в виде многочлена) за скобки. теория

Практика Вынесение общего множителя за скобки Пример: 3а + 12b = 3(а + 4 b) 2у(х - 5) + х(х – 5) = (х – 5)(2у + х) С помощью формул сокращенного умножения Пример: 4х2 + 12ху + 9у2 = (2х + 3у)2 125а3 – 64х3 = (5а – 4х)(25а2 + 20ах + 16х2) 49х4у6 - 0,01а2 = (7х2у3 – 0,1а) (7х2у3 + 0,1а) Способ группировки Пример: 3а2 +3аb – 7а - 7b = (3а2 + 3аb) – (7а + 7b) = 3а(а + b) – 7(а + b) = (а + b)(3а – 7)

Порядок разложения многочлена на множители Вынести общий множитель за скобку (если он есть) Попробовать разложить многочлен на множители по формулам сокращенного умножения Попытаться применить способ группировки (если предыдущие способы не привели к цели) Схема урока

Задачник Задания первого уровня Задания второго уровня Задания третьего уровня Схема урока

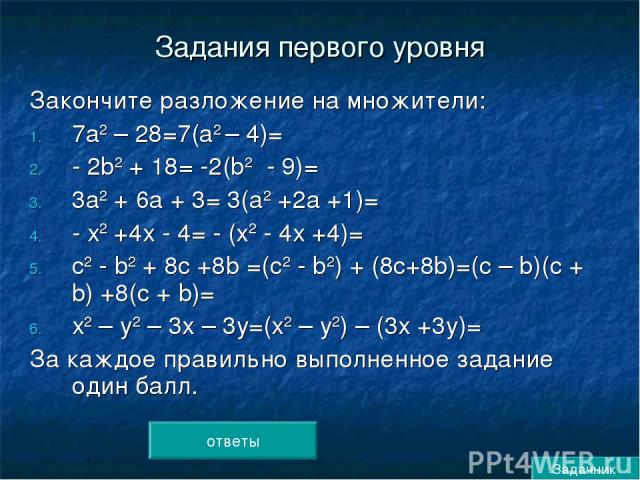
Задания первого уровня Закончите разложение на множители: 7а2 – 28=7(а2 – 4)= - 2b2 + 18= -2(b2 - 9)= 3а2 + 6а + 3= 3(а2 +2а +1)= - х2 +4х - 4= - (х2 - 4х +4)= с2 - b2 + 8с +8b =(с2 - b2) + (8с+8b)=(с – b)(с + b) +8(с + b)= х2 – у2 – 3х – 3у=(х2 – у2) – (3х +3у)= За каждое правильно выполненное задание один балл. ответы Задачник

Ответы 7(а – 2)(а +2) - 2(b – 3)(b + 3) 3(а +1)2 - (х – 2)2 (с + b)(с – b + 8) (х – у)(х + у) – 3(х + у)=(х +у)(х – у – 3)

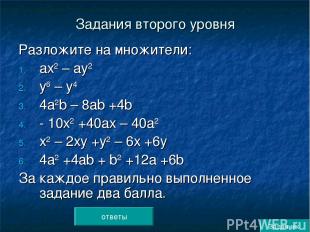
Задания второго уровня Разложите на множители: ах2 – ау2 у6 – у4 4а2b – 8аb +4b - 10х2 +40ах – 40а2 х2 – 2ху +у2 – 6х +6у 4а2 +4аb + b2 +12а +6b За каждое правильно выполненное задание два балла. ответы Задачник

Ответы: а(х – у)(х +у) (у3 – у2)(у3 + у2) 4b(а – 1)2 - 10(х – 2а)2 (х – у)(х – у – 6) (2а + b) (2а + b +6)

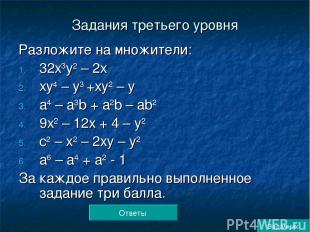
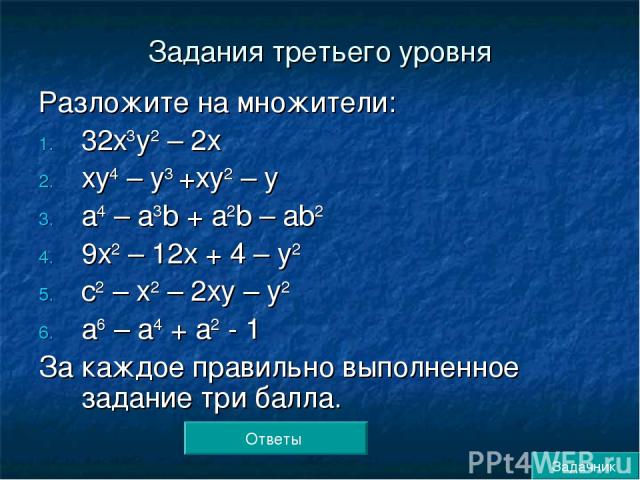
Задания третьего уровня Разложите на множители: 32х3у2 – 2х ху4 – у3 +ху2 – у а4 – а3b + а2b – аb2 9х2 – 12х + 4 – у2 с2 – х2 – 2ху – у2 а6 – а4 + а2 - 1 За каждое правильно выполненное задание три балла. Ответы Задачник

Ответы: 2х(4ху -1)(4ху +1) (у3 +у)(ух -1) (а3 – аb)(а – b) (3х - 2 – у)(3х – 2 +у) (с – х – у)(с + х + у) (а2 – 1)(а4 + 1)

Более сложный уровень. Пример: n3 +3n2 +2n= n(n2 +3n+2)= n(n2 +2n + n +2)= n((n2 +2n) + (n +2))= n(n(n +2)+(n +2))=n(n +2)(n +1) Для решения этого примера мы использовали еще один прием разложения на множители – предварительное преобразование Схема урока Задания

Предварительное преобразование Некоторый член многочлена раскладывается на необходимые слагаемые или дополняется путем прибавления к нему некоторого слагаемого. В последнем случае, чтобы многочлен не изменился, от него отнимается такое же слагаемое.

Решите уравнение: х2 +10х +21=0 х2 +10х +25 - 4=0 (х +5)2 – 4=0 (х +5 -2)(х +5 + 2)=0 (х +3)(х +7)=0 х +3 =0 или х +7 =0 х = -3 или х = -7 Ответ: -3; -7. Метод выделения полного квадрата. Сложный уровень

Сложные задания: Решите уравнение: х2 – 15х +56 =0 Докажите тождество: (а2 +3а)2 +2(а2 +3а)= а(а+1)(а+2)(а+3) 3.Разложите на множители: а)х2 – 3х +2 b)х2 + 4х +3 За каждое правильно выполненное задание 4 балла. Сложный уровень

Решите уравнение: х2 – 15х +56 =0 х2 – 7х – 8х +56 =0 (х2 – 7х) – (8х – 56) = 0 х(х – 7) – 8(х – 7) =0 (х – 7)(х – 8) =0 х -7 =0 или х – 8 =0 х=7 или х=8 Ответ: 7;8 Сложные задания

Докажите тождество: (а2 + 3а)2 +2(а2 + 3а) = а(а + 1) (а + 2)(а + 3) (а2 + 3а)2 +2(а2 + 3а) = (а2 + 3а)(а2 + 3а) + 2(а2 +3а) = (а2 + 3а)(а2 + 3а + 2) = (а(а + 3))(а2 + 2а + а + 1 +1) = а(а + 3)((а2 + 2а + 1) +(а + 1)) = а(а +3)((а + 1)2 +(а + 1)) = а(а +3)(а + 1)(а + 1 + 1) = а(а + 3)(а + 1)(а + 2) = а(а + 1)(а + 2)(а + 3) Сложные задания

Разложите на множители: а) х2 – 3х + 2 = х2 – 2х – х + 1 + 1 = (х2 – 2х + 1) – (х – 1) = (х – 1)2 – (х – 1) = (х – 1)(х – 1 – 1) = (х – 1)(х – 2) Сложные задания

Разложите на множители: b) х2 + 4х + 3 = х2 + 4х + 4 – 1 = (х2 + 4х + 4) – 1 =(х + 2)2 – 12 = (х + 2 – 1)(х + 2 + 1) = (х + 1)(х + 3) Сложные задания

Проверь себя. Разложите на множители, используя различные способы: 5а3 – 125аb2 5а(а - 5b)(а + 5b) 5а(а2 - 25 b2) 5а(а - 5b)2 63аb3 – 7а2b 7а2b2(9b – 1) аb(63 b2 – 7а) 7аb(9b2 – а) 3а2 + 6а + 3 3(а +1)(а – 1) 3(а + 1)2 (3а + 1)2 а2 - b2 + 6а +6b (а + b)(а – b + 6) ( а – b)2 (а2 - b2) + (6а + 6b) 6х2 – 12х + 6 (3х – 3)2 6(х – 1)2 (х – 1)(х + 6) Схема урока

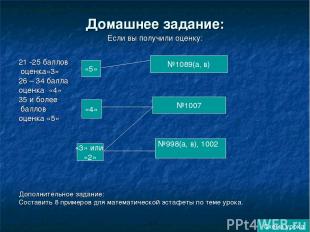
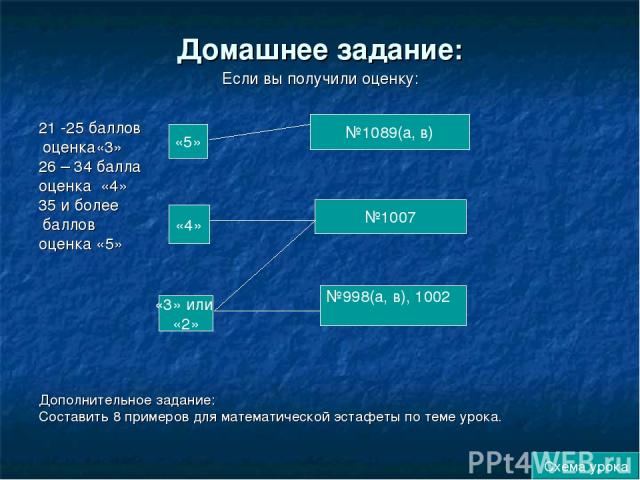
Домашнее задание: Если вы получили оценку: 21 -25 баллов оценка«3» 26 – 34 балла оценка «4» 35 и более баллов оценка «5» Дополнительное задание: Составить 8 примеров для математической эстафеты по теме урока. «4» «5» «3» или «2» №1089(а, в) №1007 №998(а, в), 1002 Схема урока