Презентация на тему: Многочлен по алгебре

Урок алгебры в 7 классе. МОУ Дятьковская СОШ №5 Учитель математики – Павликова Елена Владимировна 16.04.2010 900igr.net

О ЕГЭ давно твердят, Запугать им вас хотят. Он для вас не будет страшен, А проверит знанья ваши. В рабочих будней череде Мы подготовимся к ЕГЭ.

16.04.2010

1. ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ 1.1. Действия с дробями 1.2. Иррациональные выражения Алгоритм извлечения квадратного корня из числа Действия с иррациональными выражениями 1.3. Текстовые задачи Задачи на движение Задачи на проценты Задачи на производительность 2. ФУНКЦИИ И ИХ СВОЙСТВА 2.1. Многочлены Оглавление От авторов 8 Рекомендации по подготовке к ЕГЭ 15 Краткий теоретический справочник 32 § 1. Условные обозначения 32 § 2. Степени и корни 33 § 3. Модуль и его свойства 34 § 4. Прогрессии 35 § 5. Логарифмы 35 § 6. Тригонометрия 36 § 7. Многочлены 40 § 8. Уравнения 44 § 9. Неравенства 46

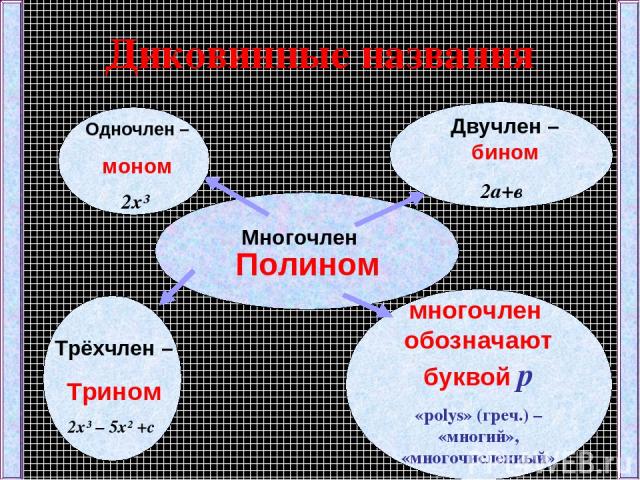
Многочлен Это сумма одночленов Одночлен Произведение числовых и буквенных множителей
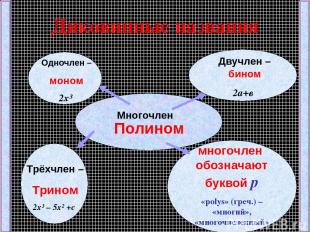
Диковинные названия Многочлен Одночлен – моном 2x³ Двучлен –бином 2а+в Трёхчлен – Трином 2x³ – 5x² +с многочлен обозначают буквой р «polys» (греч.) – «многий», «многочисленный» Полином

2 – 3 + 4 + 5 1 + 3 – 2 ____________ 2 – 2 + 7 + 3 + +



Верно ли утверждение ? Да Нет Многочленом называется сумма одночленов. Разложить многочлен на множители, значит представить этот многочлен в виде суммы более простых многочленов. Разность квадратов двух чисел (выражений) равна частному суммы этих чисел (выражений) на их разность. Одинаковые одночлены или отличающиеся друг от друга только коэффициентами, называют подобными членами многочлена. В результате деления многочлена на одночлен получается одночлен. Существует только два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки. Сумма кубов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на полный квадрат их разности. 7 - оценка «5» 6- 5 - «4» 4 - 3 - «3» менее 3 – «2»


КЛЮЧ ОТВЕТОВ: 01001 1- истина 0 – ложь 5 - оценка «5» 4 - «4» 3 - «3» менее 3 – «2» Вариант 1 (t – s)(t + s) = t2 – 2ts + s2 5a²b(4ab + 3b²) = 20a³b² + 15a²b³ 7m²–4mn–n²–(2m²–mn)=5m–3mn 2d+3cd=d(2+c) х2 - 2ху + у2 = (х - у)2 Вариант 2 (х – у)2 = х2 - ху + у2 23а+ 19b–(12а -11b+9)=11а +30b–9 3c2-6c = 3c (c-3) p² + 2pr + r2 = (p – r)(p + r) (12n³k³ – 15n² ) : (3nk) = 4n²k²–5nk³

71² = Я догадался, как можно использовать формулы для устных вычислений. 5041 960 6399 53²- 43² = 79 • 81 =


Сборник тренировочных тестов для промежуточной аттестации под редакцией Лысенко Ф.Ф. Стр. 156 Вариант №15 задание А2 Упростите выражение (4а + 3)² - (3-4а)(3+4а) 1)32а² + 24а 2) -12а² 3) 24а 4) -4а² + 24а Стр. 81 Вариант №21 задание А7 Упростите выражение (3а – 2)(а² - а +1) – (6 - 10 ):2а² и найдите его значение при а = - 6. Стр. 101 Вариант №29 задание А7 Если многочлен 4х² + ах + b можно представить в виде (4х – 3)(х+8), то сумма чисел а и b равна…


Сборник заданий для подготовки к ГИА в 9 классе под редакцией Л.В.Кузнецовой: Стр. 48 Работа № 6 вариант 1 задание №6 Укажите выражение, тождественно равное многочлену 4х² - 6ху А) -2х(-3у-2х) В) -2х(3у+2х) Б) -2х(3у-2х) Г) -2х(-2х-3у) Задание из второй части экзаменационной работы Стр. 156 №8.6.(1)
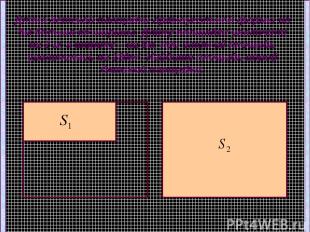
Длина детской площадки прямоугольной формы на 5м больше её ширины. Длину площадки увеличили на 2 м, а ширину – на 5м, при этом её площадь увеличилась на 280м². Найдите площадь новой детской площадки.

Длина детской площадки прямоугольной формы на 5м больше её ширины. Длину площадки увеличили на 2 м, а ширину – на 5м, при этом её площадь увеличилась на 280м². Найдите площадь новой детской площадки. х х+5 х+5+2=х+7 х+5 х(х+5) (х+7)(х+5) Длина (м) Ширина (м) Площадь (м²) 1. Исходная площадка 2. Новая площадка

1 вариант 2 вариант 1. Упростите выражение: (а-4)²-2а(3а-4) А. -5а²+16 Б. -5а²+8а-16 В. -5а²+8 Г. -5а²+8а-4 1. Упростите выражение: (с+5)²-с(10-3с) А. -2с²+25 Б. 4с²-10с+25 В. 4с²-5с+25 Г. 4с²+25 2. Решите уравнение: 2х²-8=0 А. -2; 2 Б. 0; 4 В. -2; 0; 2 Г. -8; 8 2. Решите уравнение: 3х²-27=0 А. -3; 0; 3 Б. -3; 3 В. -9; 9 Г. -27; 0 3. В выражении 8х²-12ху вынесли за скобки общий множитель -4х. Какой двучлен остался в скобках? А. -2х-3у Б. 2х-3у В. -2х+3у Г. 2х+3у 3. В выражении 9ху-6у² вынесли за скобки общий множитель -3у. Какой двучлен остался в скобках? А. -3х-2у Б. -3х+2у В. 3х-2у Г. 3х+2у 1. А 2. А 3. В 1. Г 2. Б 3. Б

16.04.2010 1 ур. - Вариант 10, часть 1 2 ур.- Вариант 10, части 1 и 2

Оцени себя и сделай для себя вывод о пользе проведенного на уроке времени Оцените урок. Я доволен уроком, мне очень понравилось, я всё понял(а). Мне понравился урок, но в моих знаниях есть пробелы. Я не доволен уроком, ничего не понял(а) и как решать, я не знаю.

Урок алгебры в 7 классе. МОУ Дятьковская СОШ №5 Учитель математики – Павликова Елена Владимировна 16.04.2010