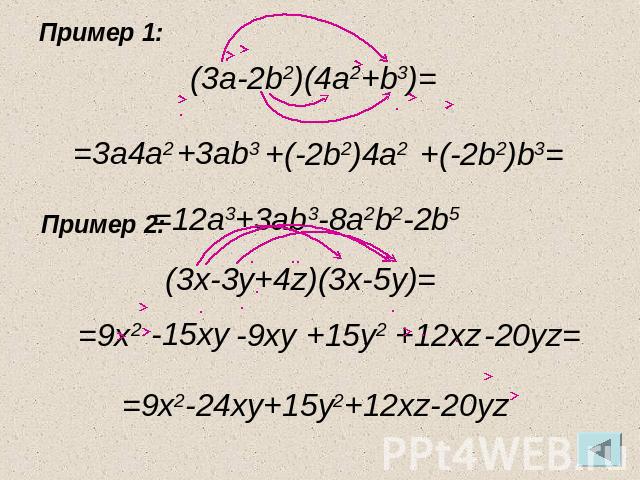Презентация на тему: Умножение многочлена на многочлен

Умножение многочлена на многочлен Курсовая работа Алевтины Алексеевны Рагимовой Лицей № 179 Калининского района

Содержание Устная работа Новый материал Примеры Работа с проверкой Самостоятельная работа

Найдите площадь и периметр данных фигур. Запишите решение в виде выражения. S=3a P=2(3+a) S=3*7 P=2(3+7) S=ca P=2(c+a) S=cd P=2(c+d)

(c+d) - ширина (b+a) - длина S=(b+a)(c+d) S1=bc S2=ac S3=bd S4=ad S=S1+S2+S3+S4 S=bc+ac+bd+ad (b+a)(c+d)=bc+ac+bd+ad

(b+a)(c+d)=bc+bd+ac+ad Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
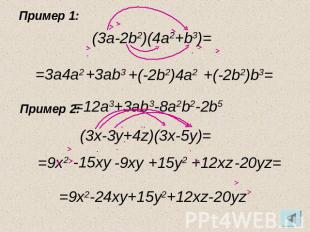
Пример 1: (3a-2b2)(4a2+b3)= =3a4a2 +3ab3 +(-2b2)4a2 +(-2b2)b3= Пример 2: =12a3+3ab3-8a2b2-2b5 (3x-3y+4z)(3x-5y)= =9x2 -15xy -9xy +15y2 +12xz -20yz= =9x2-24xy+15y2+12xz-20yz

№ 726 1 вариант (x+6)(x+5)= b) (a-4)(a+1)= (2-y)(y-8)= =x2+5x+6x+30= x2+11x+30 =a2+a - 4a - 4 = a2- 3a - 4 =2y -16 - y2+8y=10y - y2-16 2 вариант (a-4)(2a+1)= (2y-1)(3y+2)= (5x-3)(4-3x)= =2a2+a - 8a - 4=2a2-7a-4 =6y2+4y-3y-2=6y2+y-2 =20x-15x2-12+9x=29x-15x2-12

Самостоятельная работа 1 вариант (x+4)(y-5) (5y2+1)(3y2-1) (4a2+2a+1)(2a-1) 2 вариант (x-8)(y+6) (3x2-1)(2x2+1) (1+2b)(1-2b+4b2)

(b+a)(c+d)=bc+bd+ac+ad Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

(b+a)(c+d)=bc+bd+ac+ad Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.