Презентация на тему: Рациональные уравнения

Рациональные уравнения Их основные свойства и правила решения.

Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. Извне он может получить только возбуждение. А. ДистервергУравнения являются математическими моделями очень многих физических и иных явлений. Поэтому решение различных практических задач сводится к решению уравнений.Уравнением с одним неизвестным называется запись вида А(x)=B(x), в которой A(x) и B(x)-выражение от неизвестной x.Областью определения уравнения называется множество всех значений x, при которых определены обе части уравнения.Корнем или решением уравнения называется значение неизвестного, при подстановке которого в уравнение получается верное числовое равенство. Решить уравнение –значит найти все его корни или доказать, что их нет.

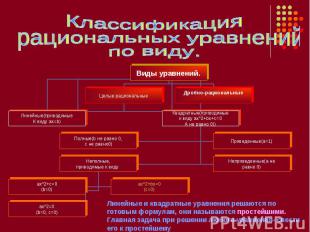
Классификация рациональных уравнений по виду.Линейные и квадратные уравнения решаются по готовым формулам, они называются простейшими. Главная задача при решении любого уравнения- свести его к простейшему

Примеры. 1) 2(x+7)=2x+14 2) 3(x-1)-5(5-x)=7 3) (a^2-9)x=a^2-5a+6 4) 2x+5-x=8x Уравнение 1 имеет бесконечное множество корней, уравнение 2- решений не имеет,уравнение4 имеет один корень, уравнение 3- линейное уравнение с параметром; в зависимости от значения параметра а уравнение может иметь различное количество корней.Решим уравнение 3:Случай1. а^2-9=0.Тогда а=-3 или а=3. Если а=-3, то исходное уравнение примет вид 0x=30 и корней не имеет. Если а=3, то получим уравнение 0x=0, для которого любое действительное число является корнем.Случай2.(a^2-9) не равно 0. Т.е. получаем что а не принадлежит (-3;3). Тогда мы выражаем x через а. Получаем: х = (а-2)/(а+3)Решить уравнение с параметром а- это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

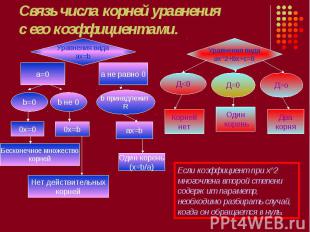
Связь числа корней уравненияс его коэффициентами.Если коэффициент при х^2 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.

Запомни!!!Основными рациональными уравнениями с одной переменной являются линейные и квадратные уравнения. Все остальные рациональные уравнения приводятся с помощью различных преобразований к этим основным.Два уравнения называются равносильными, если они имеют одинаковые корни или оба уравнения не имеют корней.Уравнение Y2 называется следствием уравнения Y1, если любой корень Y1 является корнем Y2.Если исходное уравнение преобразуется в равносильное уравнение, то никакой особой проверки решения уравнения не требуется. Если же исходное уравнение преобразуется в процессе решения в уравнение-следствие, то обязательна проверка всех найденных корней.

Методы решения рациональных уравнений. Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречномуБолее часто используются методыРазложения на множители и введениеНовых переменных!

Метод разложения на множителиСуть этого метода заключается в следующем: уравнение f1(x)f2(x)f3(x)=0 можно заменить совокупностью уравнений: f1(x)=0; f2(x)=0; f2(x)=0. Решив уравнение этой совокупности, возьмите их корни, которые принадлежат области определения исходного уравнения, а остальные отбросьте как посторонние.Метод разложения на множители включает в себя:Способ группировки.Вынесение общего множителя за скобки.Использование формул сокращенного умножения.Способ выделения полного квадрата.Разложение квадратного трехчлена aх^2+bx+c=a(x-x1)(x-x2),где x1, x2- корни этого трехчлена.

Графический метод. Сформулируем идею графического метода решения уравненияf(x)=g(x):Необходимо построить графики функций y=f(x), y=g(x)Найти точки пересечения – корнями уравнения служат абсциссы этих точек. В каких случаях лучше использовать этот метод?Когда необходимо определить число корней уравнения, угадать значение корня, найти приближенные значения корней Графические способы решения красивы, просты, но не дают стопроцентной гарантии решения любого рационального уравнения.

Метод введения новых переменных. Удачный выбор новой переменной делает структуру уравнения более прозрачной.Суть метода введения новых переменных:Если уравнение f(x)=0 удалось преобразовать к виду z(g(x))=0, то нужно ввести новую переменную y=g(x), решить уравнение z(y)=0, а затем рассмотреть совокупность уравнений: g(x)=y1, g(x)=y2, … g(x)=yn где y1,y2,…yn- корни уравнения z(y)=0Новая переменная в уравнениях иногда действительно очевидна, но иногда ее трудно увидеть, а можно выявить лишь в процессе каких- либо преобразований.