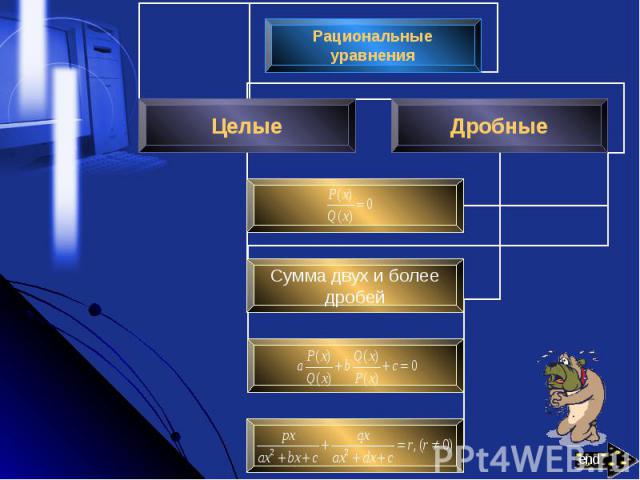
Презентация на тему: Рациональные уравнения


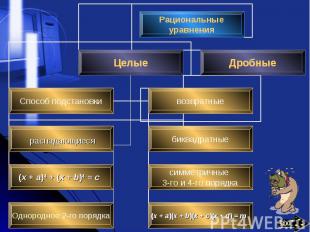
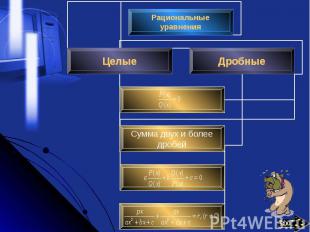

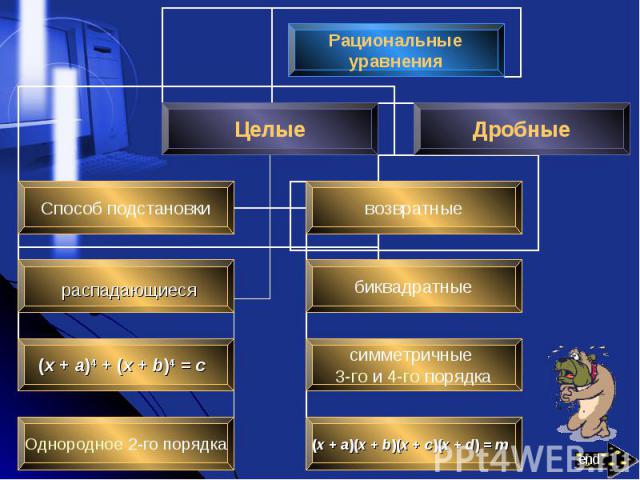
При решении некоторых целых рациональных уравнений есть смысл ввести новую переменную величину, обозначив некоторое рациональное выражение новой буквой. При решении некоторых целых рациональных уравнений есть смысл ввести новую переменную величину, обозначив некоторое рациональное выражение новой буквой. Например, в уравнении , где Р(х) – многочлен, удобно ввести новую переменную y=Р(х), решить полученное квадратное уравнение относительно y и, наконец, решить уравнение Р(х)= yо, где yо – корень уравнения

Решите уравнение Решите уравнение Решение. Введем новую переменную. Пусть Тогда получим уравнение Находим корень у = 1 и делаем обратную подстановку. Ответ: 2; 3.

Рациональное уравнение называется распадающимся, если его можно привести к виду , где – рациональные выражения с переменной х. Рациональное уравнение называется распадающимся, если его можно привести к виду , где – рациональные выражения с переменной х. Для решения воспользуемся равносильным переходом Применяемые приемы разложения на множители: - вынесение общего множителя за скобки; - способ группировки; -формулы сокращенного умножения.

Решите уравнение Решите уравнение Решение. Разложим левую часть уравнения на множители: Воспользуемся равносильным переходом: Ответ:-2;0;1;2.

При решении уравнения надо проверить две ситуации: При решении уравнения надо проверить две ситуации: 1) т.е. корнями заданного уравнения являются решения этой системы. 2) Если Q(x) ≠ 0, то после деления заданного уравнения на Q2(x) получим уравнение которое подстановкой сводится к квадратному уравнению В ответ включают числа, полученные при рассмотрении обеих ситуаций.

Решить уравнение Решить уравнение (x2 – 2х)2 – (x2 – 2х)(x2 – х – 2) – 2(x2 – х – 2)2 = 0. Решение. Возможны две ситуации. Рассмотрим первую:

Рассмотрим вторую ситуацию: разделим почленно заданное уравнение на (x2 – х – 2)2 при условии, что х ≠ -1 и х ≠ 2. Уравнение принимает вид Рассмотрим вторую ситуацию: разделим почленно заданное уравнение на (x2 – х – 2)2 при условии, что х ≠ -1 и х ≠ 2. Уравнение принимает вид Обозначим и решим квадратное уравнение t2 – t –2 = 0. Получаем t1= -1, t2= 2. Обратная подстановка дает уравнения откуда х = -0,5 и х = -2. С учетом обеих ситуаций получаем ответ: - 0,5; -2; 2.

Уравнение имеет вид Уравнение имеет вид aх4+bх2+c=0. Сделаем подстановку x2 = t. Значит, x4 = t2. Получаем квадратное уравнение at2+bt+c=0. Находим значения t и, сделав обратную подстановку, находим корни исходного уравнения. Замечание. При решении биквадратного уравнения можно получить от 1 до 4-х корней или же это уравнение может совсем не иметь корней.

Решите уравнение х4–3х2–4=0. Решите уравнение х4–3х2–4=0. Решение. Сделаем подстановку x2 = t. Получаем квадратное уравнение t2–3t–4=0, корни которого t = -1 и t = 4. Обратная замена дает два уравнения x2 = -1 и x2 = 4, из которых первое уравнение не имеет корней, а корни второго уравнения -2 и 2. Ответ: -2; 2.

Уравнение имеет вид Уравнение имеет вид ах3+bх2+bх+а=0. Сгруппируем слагаемые: а(х3+1)+bх(х+1)=0. Применим формулу суммы кубов а(х+1)(х2 –х+1)+bх(х+1)=0 и выполним разложение на множители (х+1)(ах2+(b - а)х+а)=0. Получили распадающееся уравнение. Значит, х+1=0 или ах2+(b - а)х+а=0. Решив эти два уравнения, найдем корни исходного уравнения.

Решите уравнение 2х3–3х2– 3х +2=0. Решите уравнение 2х3–3х2– 3х +2=0. Решение. Сгруппируем слагаемые парами и в каждой паре вынесем общий множитель за скобки: 2(х3+1)–3х(х+1)=0. Применим формулу суммы кубов и вынесем общий множитель (х+1): 2(х+1)(х2 –х+1)– 3х(х+1)=0, (х+1)(2х2 –5х+2)=0. Значит, х+1=0 или 2х2 –5х+2=0. Решив эти два уравнения, найдем корни исходного уравнения: -1; 0,5; 2. Ответ: -1; 0,5; 2.

Уравнение имеет вид Уравнение имеет вид ах4+bх3+сх2+bх+а=0. Сгруппируем слагаемые и разделим обе части уравнения на х2. Получаем Сделаем подстановку , тогда Получаем квадратное уравнение a(t2-2)+bt+c=0. Находим значения t и делаем обратную подстановку.

Решите уравнение Решите уравнение Решение. Разделим обе части уравнения на x2 ≠ 0 и, удобно группируя, получим равносильное уравнение: Сделаем подстановку , тогда Получаем квадратное уравнение , корни которого 2 и -3,5. Обратная подстановка дает два рациональных уравнения и откуда и находим корни исходного уравнения. Ответ: 1;

Уравнение вида Уравнение вида ax4 + bx3 + cx2 + dx + e = 0, где a ≠ 0, b ≠ 0 и , называется возвратным уравнением четвертого порядка. Это уравнение сводится к квадратному с помощью подстановки

Решить уравнение Решить уравнение x4 + x3 - 6x2 - 2x + 4 = 0. Решение. Заметим, что и, следовательно, данное уравнение есть возвратное уравнение четвертого порядка. Так как x = 0 не является решением уравнения, разделим на x2 и получим равносильное уравнение Обозначим , тогда и уравнение примет вид t2 + t - 2 = 0, корни которого t1 = -2 и t2 = 1. Делаем обратную замену и после умножения на x ≠ 0 получаем два квадратных уравнения x2 + 2x - 2 = 0, x2 - x - 2 = 0, откуда и получим корни исходного уравнения. Ответ:

Если a + b = c + d , то это уравнение сводится к квадратному уравнению. Действительно, Если a + b = c + d , то это уравнение сводится к квадратному уравнению. Действительно, (x + a)(x + b) = x2 + (a + b)x + ab (x + c)(x + d) = x2 + (c + d)x + cd = = x2 + (a + b)x + cd Обозначив x2 + (a + b)x = t, получим квадратное уравнение (t + ab)(t + cd) = m Из этого уравнения найдем значения t и, сделав обратную подстановку, закончим решение исходного уравнения.

Решить уравнение Решить уравнение (x - 2)(x + 1)(x + 4)(x + 7) = 19. Решение. Заметим, что -2 + 7 = 1 + 4. Удобно группируя, получим [(x - 2)(x + 7)]·[(x + 1)(x + 4)] = 19 или (x2 + 5x – 14 )(x2 + 5x + 4) = 19. Обозначим t = x2 + 5x - 14, тогда x2 + 5x + 4 = t + 18. Уравнение примет вид t(t + 18) = 19 или t2 + 18t - 19 = 0, откуда t = -19 и t = 1. Сделав обратную подстановку, получим x2 + 5x - 14 = -19 и x2 + 5x - 14 = 1. Окончательный ответ:

Используя подстановку , уравнение Используя подстановку , уравнение можно свести к биквадратному уравнению относительно t. Действительно, подставив в уравнение , получим Обозначим и возведем каждое слагаемое в 4-ю степень. После приведения подобных получим биквадратное уравнение

Решить уравнение Решить уравнение (x + 3)4 + (x - 1)4 = 82. Решение. Сделаем подстановку Получим следующее уравнение относительно t: (t + 2)4 + (t - 2)4 = 82 или t4 + 8t3 + 24t2 + 32t + 16 + t4 - 8t3 + 24t2 - 32t + 16 - 82 = 0. Откуда получим биквадратное уравнение t4 + 24t2 - 25 = 0, корни которого t = ± 1. Следовательно, x + 1 = ± 1. Значит, корни исходного уравнения x = -2 и x = 0. Ответ: -2;0.

Решить уравнение Р(х) = 0. Решить уравнение Р(х) = 0. Для каждого корня уравнения Р(х) = 0 сделать проверку: удовлетворяет ли он условию Q(х) ≠ 0 или нет. Если да, то это — корень заданного уравнения, а если нет, то этот корень является посторонний для заданного уравнения и в ответ его включать не следует.

Решите уравнение Решите уравнение Решение. Приравняем числитель дроби к нулю и решим полученное уравнение: Значение х = 2 не удовлетворяет условию Следовательно, уравнение имеет один корень х= 4. Ответ: 4.

Подстановкой это уравнение Подстановкой это уравнение сводится к виду Умножим на и решим полученное квадратное уравнение относительно t. Остается сделать обратную подстановку где tо - корень квадратного уравнения, и решить полученное уравнение относительно х.

Подстановкой это уравнение Подстановкой это уравнение сводится к виду Умножим на и решим полученное квадратное уравнение относительно t. Остается сделать обратную подстановку где tо - корень квадратного уравнения, и решить полученное уравнение относительно х.

Решите уравнение Решите уравнение Решение. Сделаем подстановку и решим полученное уравнение относительно t : Обратная подстановка приводит к уравнению корень которого х = -1. Ответ: -1.

1-й способ Перенести все члены уравнения в одну часть. Привести уравнение к виду и найти корни полученного уравнения. 2-й способ Определить О.Д.З. уравнения. Умножить обе части уравнения на общий знаменатель дробей и получить целое уравнение. Найти корни полученного уравнения и проверить их соответствие О.Д.З.

Решите уравнение Решите уравнение Решение. Найдём О.Д.З. Знаменатели дробей не могут обращаться в нуль . Значит, О.Д.З. уравнения: х ≠ 2 и х ≠ 0. Перенесём члены из правой части уравнения в левую и приведём к общему знаменателю. . Приравняем числитель дроби к нулю: х2 – 6х + 8 = 0. Находим корни квадратного уравнения: х = 4 и х = 2. Значение х = 2 не удовлетворяет О.Д.З. Следовательно, уравнение имеет один корень х= 4. Ответ: 4.

Данное уравнение сводится к квадратному уравнению заменой переменной Данное уравнение сводится к квадратному уравнению заменой переменной

Решить уравнение Решить уравнение Решение. О.Д.З. уравнения есть множество Поскольку x = 0 не является решением данного уравнения, перепишем уравнение в виде (разделим числитель и знаменатель каждой дроби на x). Обозначим и уравнение примет вид

О.Д.З. полученного уравнения t ≠ 5 и t ≠ -1. О.Д.З. полученного уравнения t ≠ 5 и t ≠ -1. Решая это уравнение, приходим к квадратному уравнению 2t2 - 13t + 11 = 0, корни которого t1 = 1 и t2 = 11/2 удовлетворяют О.Д.З.. Делаем обратную подстановку и получаем два рациональных уравнения решив которые находим корни заданного уравнения. Ответ:

Алгебра и математический анализ, 10 Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд Алгебра и математический анализ, 10 Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд Алгебра и начала анализа. 8 – 11 кл. Пособие для школ и классов с углубл. изучением математики (серия «Дидактические материалы») Звавич Л.И., Шляпочник Л.Я., Чинкина М.В.



















![Решить уравнение Решить уравнение (x - 2)(x + 1)(x + 4)(x + 7) = 19. Решение. Заметим, что -2 + 7 = 1 + 4. Удобно группируя, получим [(x - 2)(x + 7)]·[(x + 1)(x + 4)] = 19 или (x2 + 5x – 14 )(x2 + 5x + 4) = 19. Обозначим t = x2 + 5x - 14, тогда x2 +… Решить уравнение Решить уравнение (x - 2)(x + 1)(x + 4)(x + 7) = 19. Решение. Заметим, что -2 + 7 = 1 + 4. Удобно группируя, получим [(x - 2)(x + 7)]·[(x + 1)(x + 4)] = 19 или (x2 + 5x – 14 )(x2 + 5x + 4) = 19. Обозначим t = x2 + 5x - 14, тогда x2 +…](https://fs1.ppt4web.ru/images/95369/121225/640/img20.jpg)