Презентация на тему: Методы решения тригонометрических уравнений (10 класс)

Обобщающий урок по теме:«Методы решения тригонометрических уравнений» 10 класс Горбунова Вера Александровна, учитель физики и математикиМБОУ Черемуховская СОШ Новошешминского муниципального района РТ

«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» Я. А. Коменский

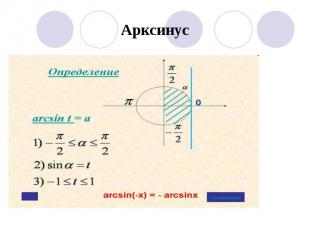
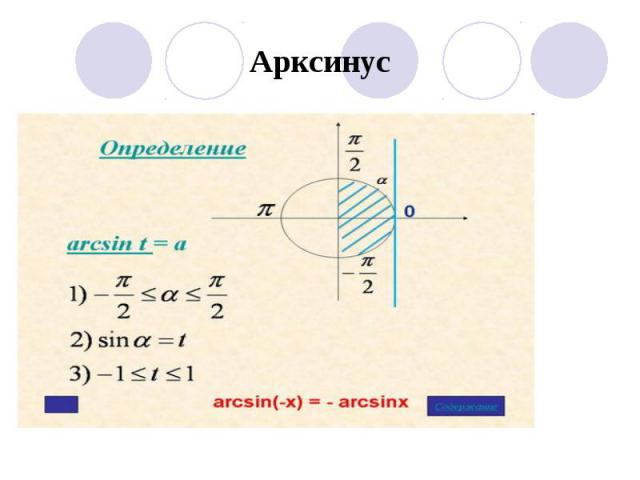
Арксинус

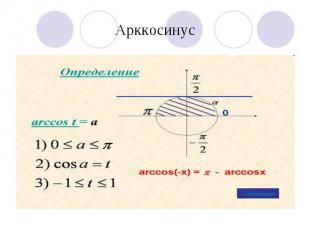
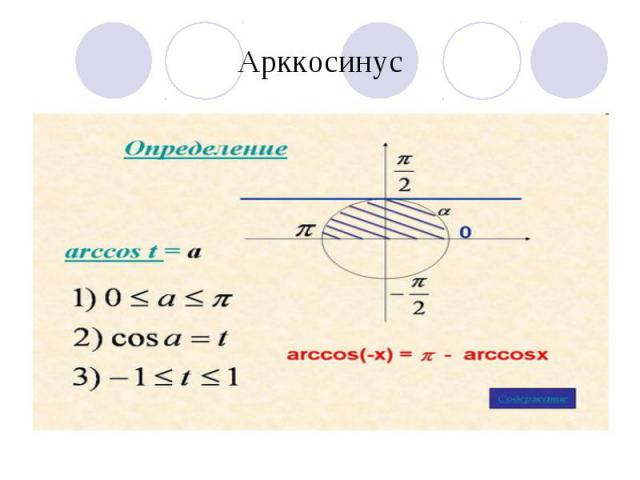
Арккосинус

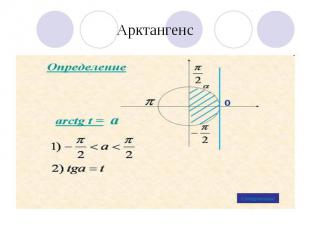
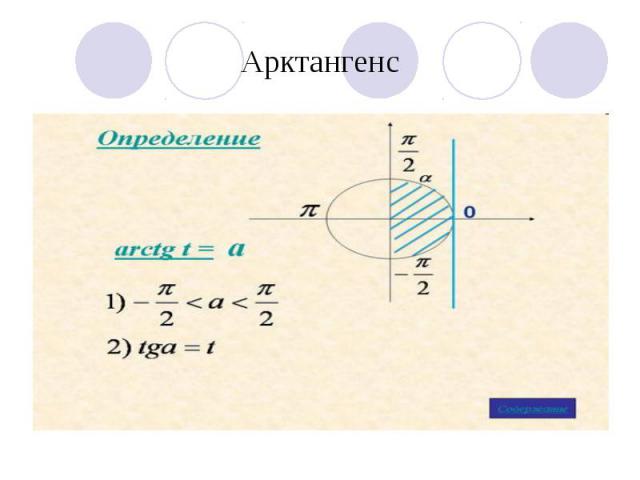
Арктангенс

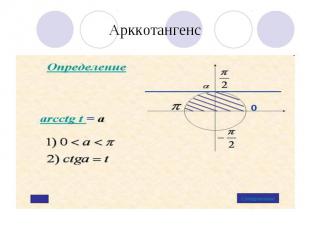
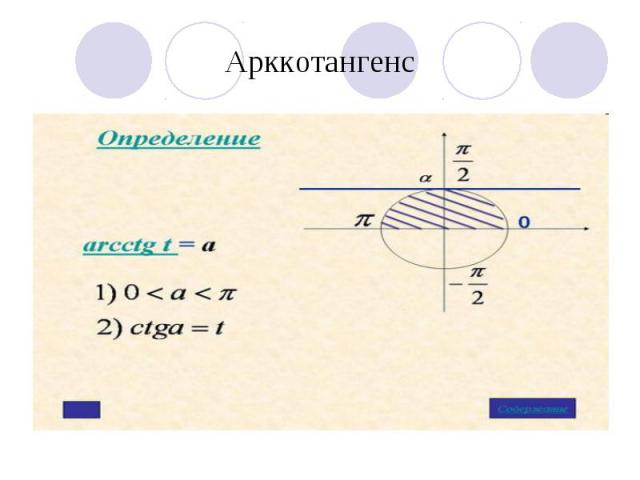
Арккотангенс

Финк- Райт – Раунд - Робин arcsin √2/2arccos 1arcsin (- 1/2 )arccos (- √3/2)arctg √3

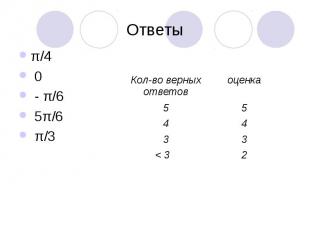
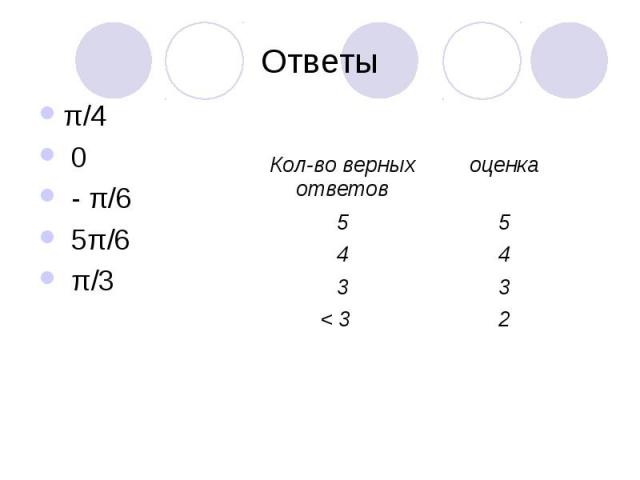
Ответы π/4 0 - π/6 5π/6 π/3

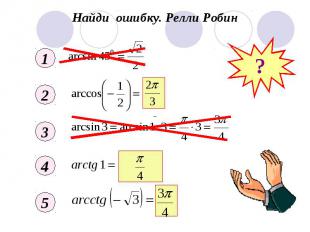
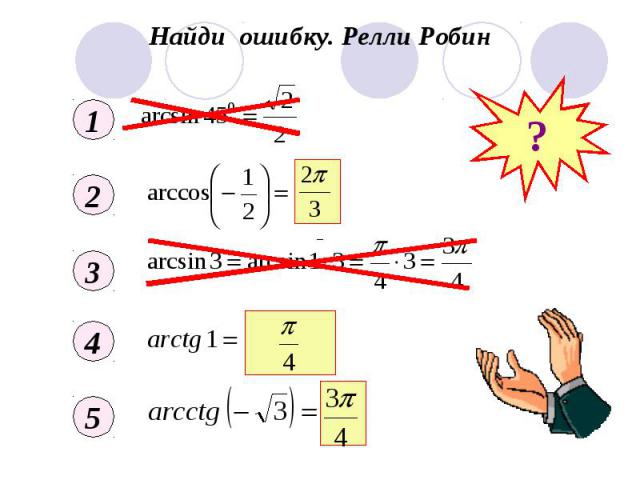
Найди ошибку. Релли Робин

Оценка

Общая схема исследования функции1. Область определения функции.2.  Исследование области значений функции3. Исследование функции на четность. 4.. Исследование функции на периодичность5. Формулы корней тригонометрических уравнений.

Функция у = sin x. 1. Областью определения функции является множество всех действительных чисел ( R )2. Областью значений) - [ - 1; 1 ].3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α4. Функция периодическая, с главным периодом 2π

Функция у = соs x. 1. Областью определения функции является множество всех действительных чисел ( R )2. Областью изменений (Областью значений) - [ - 1; 1 ]3. Функция у = cos α четная, т.к. cos (- α) = cos α4. Функция периодическая, с главным периодом 2π.

Функция у = tg x 1. Областью определения функции является множество (- π/2; π/2)2. Областью значений R.3.Функция у = tg x нечетная, т.к. tg (- α) = - tg α4. Функция периодическая, с главным периодом π.

Функция у = ctg x 1. Областью определения функции является множество (πn; π + πn)2. Областью значений R3. Функция у = ctg x нечетная, т.к. ctg (- α) = - ctg α4. Функция периодическая, с главным периодом π.

Клок Бадис Пример 1. sin x = −Пример 2. cos x = Пример 3. tg x = − 1Пример 4. ctg x =

Пример 1 sin x = −

Пример 2 cos x =

Пример 3 tg x = − 1

Пример 4 сtg x =

Оценка

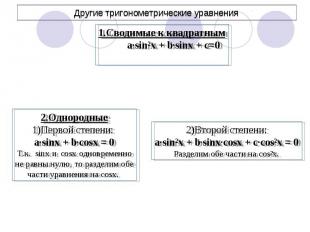
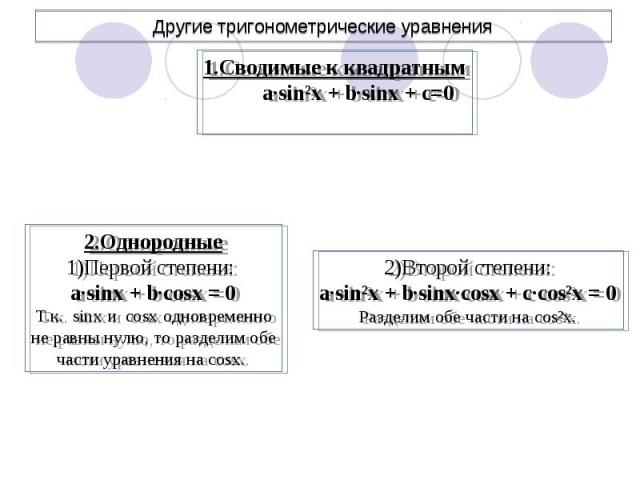
Другие тригонометрические уравнения 1.Сводимые к квадратным a∙sin²x + b∙sinx + c=02.Однородные1)Первой степени: a∙sinx + b∙cosx = 0Т.к. sinx и cosx одновременноне равны нулю, то разделим обечасти уравнения на cosx. 2)Второй степени:a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0Разделим обе части на cos²x.

Содержание Метод замены переменной Метод разложения на множителиС помощью тригонометрических формул:Формул сложенияФормул приведенияФормул двойного аргумента

Основные методы решения тригонометрических уравнений. Домашнее задание. На «3»1) 3 sin x+ 5 cos x = 02) 5 sin2 х - 3 sinх cos х - 2 cos2х =0 На «4»1) 3 cos2х + 2 sin х cos х =02) 5 sin2 х + 2 sinх cos х - cos2х =1На «5»1) 2 sin x - 5 cos x = 32) 1- 4 sin 2x + 6 cos2х = 0 На «3»1) cos x+ 3 sin x = 02) 6 sin2 х - 5 sinх cos х + cos2х =0 На «4»1) 2 sin2 x – sin x cosx =02) 4 sin2 х - 2sinх cos х – 4 cos2х =1На «5»1) 2 sin x - 3 cos x = 42) 2 sin2 х - 2sin 2х +1 =0

« То, что мы знаем, - ограниченно, а то чего мы не знаем, - бесконечно». Пьер Лаплас:

Спасибо!

Билетик на выход а)2 cos2х + 5 sin х - 4=0 б)3 sin x - 2 cos2x =0