Презентация на тему: Методы решения тригонометрических уравнений


1.Приведение уравнения к однородному. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. 3.Введение вспомогательного угла. 4.Преобразование разности (или суммы) тригонометрических функций в произведение. 5.Приведение к квадратному уравнению. 6.Возведение обеих частей уравнения в квадрат. 7.Универсальная подстановка. 8.Графическое решение.





Покажем однозначность ответов.



Сделаем проверку. Сделаем проверку.


Выражение всех функций через (универсальная подстановка) Выражение всех функций через (универсальная подстановка) по формулам:

Область допустимых значений первоначального уравнения - всё множество R . При переходе к tg из рассмотрения выпали значения x, при которых tg не имеет смысла, т.е.x = + n, где n Z . Следует проверить , не является ли x = + n, где n Z решением данного уравнения. Левая часть sin(π - 2πk) – cos(π + 2πk) = sin π – cos π = 0 – (-1) = 1 и правая часть равна единице. Значит, x = + n ,где n Z является решением данного уравнения. Ответ: : x= + n, n Z, x= + n, n Z.
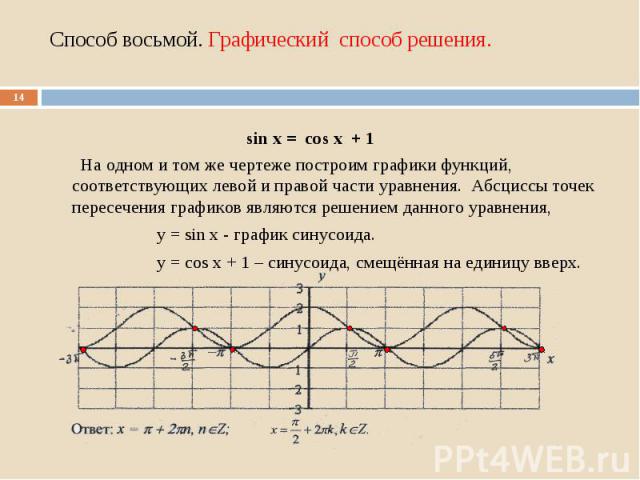
На одном и том же чертеже построим графики функций, соответствующих левой и правой части уравнения. Абсциссы точек пересечения графиков являются решением данного уравнения, у = sin х - график синусоида. у = соs х + 1 – синусоида, смещённая на единицу вверх.

Решите самостоятельно, применяя разные способы решения одного и того же тригонометрического уравнения: Решите самостоятельно, применяя разные способы решения одного и того же тригонометрического уравнения: sin2x +cos2x = 1

sin 2x + cos 2x = 1 sin 2x + cos 2x = 1 2 sin x cos x + cos 2 x – sin2 x = sin 2x + cos 2x, 2 sin x cos x – 2 sin 2 x = 0, 2 sin x ( cos x – sin x ) = 0, sin x = 0, cos x – sin x = 0, x = n, n Z, tg x = 1, Ответ: x = n, n Z, Способ: Приведение уравнения к однородному( 1-й способ ).

sin 2x + cos 2x = 1, sin2x – (1 – cos 2x ) = 0, 2 sin x cos x – 2 sin 2x = 0, Далее так, как первым способом. Способ: разложение левой части уравнения на множители ( 2 – й способ ).

Способ: преобразование суммы тригонометрических функций в произведение ( 4-й способ).

разделим обе части уравнения на , разделим обе части уравнения на , Способ: введение вспомогательного угла (3-й способ).

возведём обе части уравнения в квадрат, тогда Способ: приведение к квадратному уравнению относительно ( 5-й способ).

sin 2x + cos2x = 1, sin 2x + cos2x = 1, sin 2 2x + 2sin 2x cos2x +cos2x = 1, 2sin 2x cos2x + 1 = 1, 2sin 2x cos2x = 0, sin 2x = 0, cos2x = 0 , 2x = n, n Z ; 2x = + n, n Z, x = , n Z ; x = + , n Z. Ответ: x= , n Z; x = + , n Z. Способ : возведение обеих частей уравнения в квадрат ( 6 – й способ ).

Способ: универсальная подстановка (7-й способ).

Реши уравнения: Ответы: Реши уравнения: Ответы: