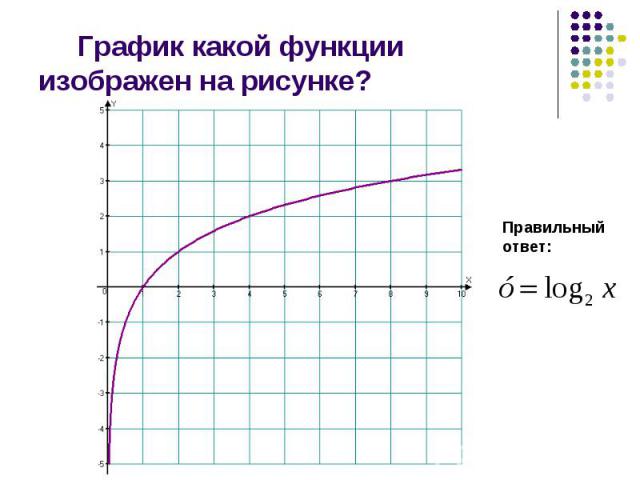
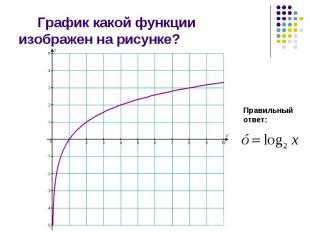
Презентация на тему: Логарифмические неравенства (2)

Повторить свойства логарифмической функции. Повторить свойства логарифмической функции. Применять эти свойства при решении логарифмических неравенств.

log26 … log210 log26 … log210 log0,36 … log0,310

Логарифмическим неравенством называют неравенство вида Логарифмическим неравенством называют неравенство вида logа f(x)>logа g(x), где a>0, a≠1, и неравенства, сводящиеся к этому виду.

Если f(x) >0 и g(x)>0, то: Если f(x) >0 и g(x)>0, то: При а>1, неравенство logа f(x)>logа g(x) равносильно неравенству того же смысла: f(x) > g(x). При 0<а<1, неравенство logа f(x)>logа g(x) равносильно неравенству противоположного смысла: f(x) < g(x). ≠

Если а>1, Если а>1, то logа f(x)>logа g(x) Если 0<а<1, то logа f(x)>logа g(x)