Презентация на тему: Логарифмические неравенства

Логарифмические неравенства

При изучении логарифмических функций рассматриваются неравенства вида: logax < b logax ≥ b
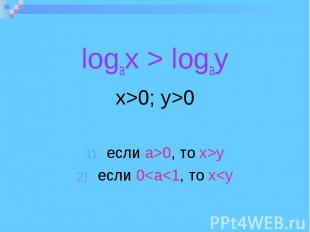
logax > logay x>0; y>0 eсли а>0, то x>y eсли 0

Пример №1 Решить неравенство: log 3(x+2) функция возрастает x+2

Пример №2 Решить неравенство:log0,5(2x+1)>-2 a=0,5; 0 log0,54 2x+1
![Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1] Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1]](https://fs1.ppt4web.ru/images/17985/103587/310/img5.jpg)
Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1]
![log2x≤1 ответы: (0;2] log3x log2x≤1 ответы: (0;2] log3x](https://fs1.ppt4web.ru/images/17985/103587/310/img6.jpg)
log2x≤1 ответы: (0;2] log3x

Решите неравенства: log3(x-2)>1 a>1 = >функция возрастает x-2>3 x-2>3 x>5 x-2>0 x>2 ответ: (5;∞) log2(x-3)>5 a>1 = >функция возрастает x-3>32 x-3>32 x>35 x-3>0 x>3 ответ: (35;∞)

lg(x-3)≥2 a>1 = >функция возрастает x-3≥100 x-3≥100 x≥103 x-3>0 x>3 ответ: [103;∞) lg(x-1)≤0 a>1 = >функция возрастает x-1≤1 x-1 ≤1 x ≤2 x-1>0 x>1 ответ: (1;2]



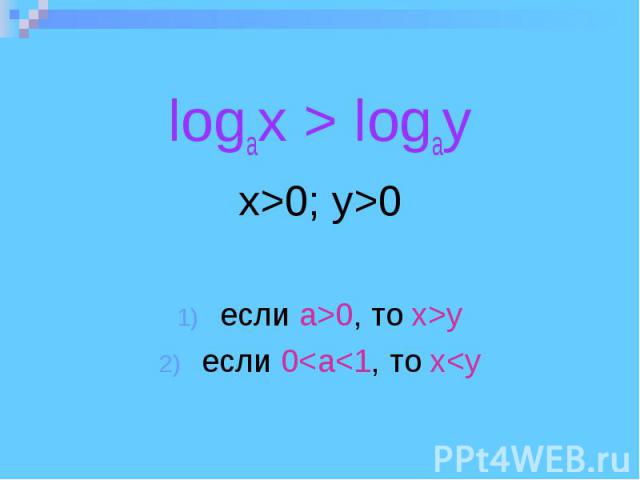


![Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1] Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1]](https://fs1.ppt4web.ru/images/17985/103587/640/img5.jpg)
![log2x≤1 ответы: (0;2] log3x log2x≤1 ответы: (0;2] log3x](https://fs1.ppt4web.ru/images/17985/103587/640/img6.jpg)

![lg(x-3)≥2 a>1 = >функция возрастает x-3≥100 x-3≥100 x≥103 x-3>0 x>3 ответ: [103;∞) lg(x-1)≤0 a>1 = >функция возрастает x-1≤1 x-1 ≤1 x ≤2 x-1>0 x>1 ответ: (1;2] lg(x-3)≥2 a>1 = >функция возрастает x-3≥100 x-3≥100 x≥103 x-3>0 x>3 ответ: [103;∞) lg(x-1)≤0 a>1 = >функция возрастает x-1≤1 x-1 ≤1 x ≤2 x-1>0 x>1 ответ: (1;2]](https://fs1.ppt4web.ru/images/17985/103587/640/img8.jpg)