Презентация на тему: Алгебраические комедии софизмы

Алгебраические комедии софизмы

«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» (Ян Амос Коменский, ХVΙ в.)

Можно разыграть настоящие алгебраические комедии и фарсы на такие сюжеты, как 2 * 2 = 5, 1 + 1 = 3 и т.п.. Юмор подобных математических представлений кроется в том, что ошибка –довольно элементарная – несколько замаскирована и не сразу бросается в глаза.

1+1=3 4 – 10 = 9 – 15 / + 6 ¼ 4 – 10 + 6 ¼ = 9 – 15 + 6 ¼ 22 – 2*2 * 5/2 + (5/2)2= 32 – 2* 3* 5/2+ (5/2)2 (2 – 5/2)2 = (3 – 5/2)2 Значит, 2 – 5/2 = 3 – 5/2 /+ 5/2 2 – 5/2 + 5/2 = 3 – 5/2 + 5/2 2 = 3 1 + 1 = 3, ч.т.д.

В чем же кроется ошибка? Решение: Ошибка проскользнула в следующем заключении: Из того, что (2 – 5/2)2=(3 - 5/2)2. Был сделан вывод, что 2 – 5/2 = 3 – 5/2. Но из того, что квадраты равны, вовсе не следует, что равны первые степени. Ведь (-5)2 = 52, но -5 не равно 5. В нашем примере мы имеем именно такой случай: (2 – 5/2)2 = (3 – 5/2)2 (- ½)2 = (1/2)2, но - ½ не равно ½

Другой алгебраический фарс 2 * 2 = 5

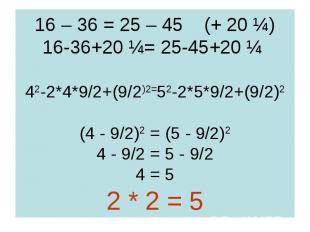
16 – 36 = 25 – 45 (+ 20 ¼) 16-36+20 ¼= 25-45+20 ¼ 42-2*4*9/2+(9/2)2=52-2*5*9/2+(9/2)2 (4 - 9/2)2 = (5 - 9/2)2 4 - 9/2 = 5 - 9/2 4 = 5 2 * 2 = 5

Эти комические случаи должны предостеречь малоопытного математика от неосмотрительных операций с уравнениями.