Презентация на тему: Кратчайший путь

Графы: определения и примеры Графы: определения и примеры Ориентированные графы Путь в орграфе Матрица смежности Иерархический список Алгоритм Дейкстры Программа “ProGraph” Описание работы программы Достоинства программы Список литературы

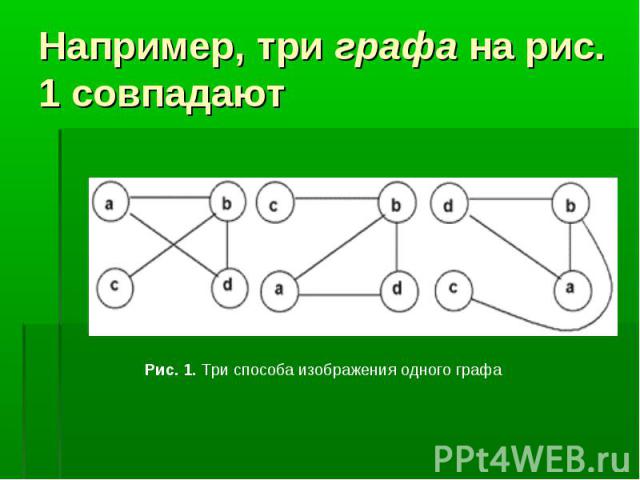
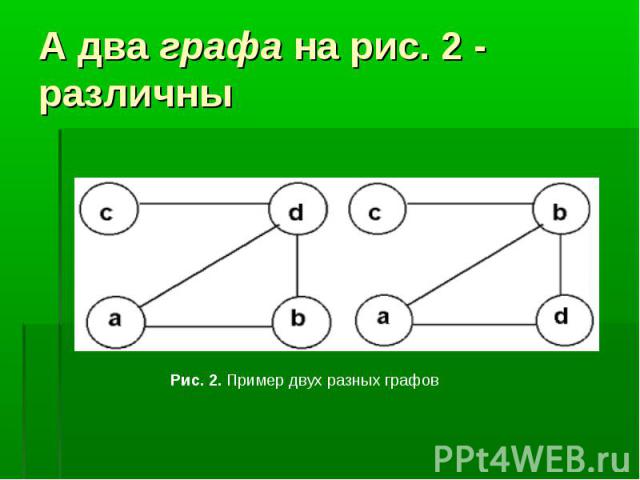
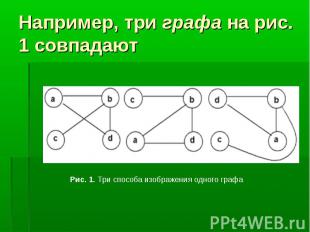
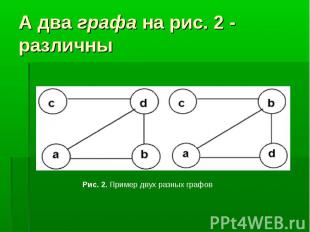
Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит. Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит.

Любому ребру соответствует ровно две вершины, а вот вершине может соответствовать произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет ребер (ее степень равна 0). Любому ребру соответствует ровно две вершины, а вот вершине может соответствовать произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет ребер (ее степень равна 0).

Две вершины называются смежными, если они являются разными концами одного ребра. Две вершины называются смежными, если они являются разными концами одного ребра. Два ребра называются смежными, если они выходят из одной вершины.

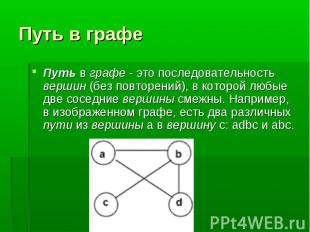
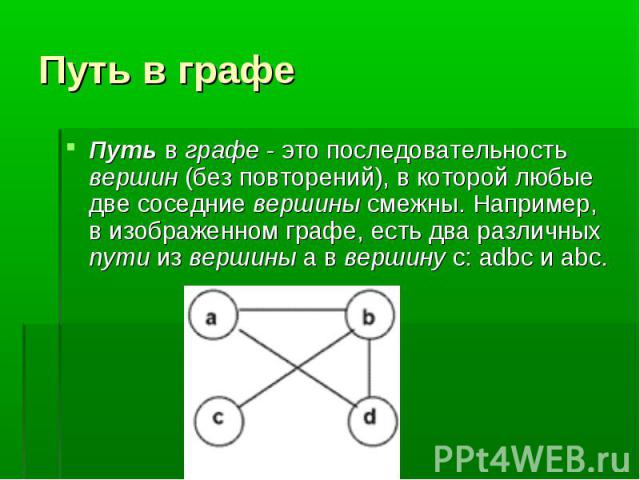
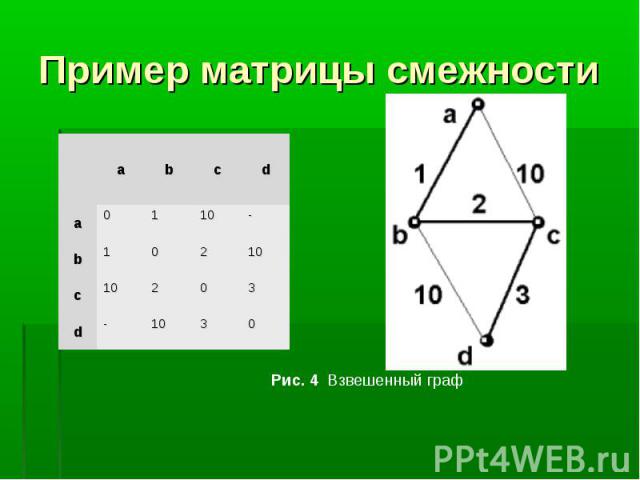
Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в изображенном графе, есть два различных пути из вершины a в вершину с: adbc и abc. Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в изображенном графе, есть два различных пути из вершины a в вершину с: adbc и abc.

Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v. Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v. Граф называется связным, если все его вершины взаимно достижимы.

Длина пути - количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc - 3 и 2 соответственно. Длина пути - количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc - 3 и 2 соответственно. Расстояние между между вершинами u и v - это длина кратчайшего пути от u до v. Из этого определения видно, что расстояние между вершинами a и c в графе на рис. равно 2. Цикл - это замкнутый путь. Все вершины в цикле, кроме первой и последней, должны быть различны. Например, циклом является путь abda в графе на рис.

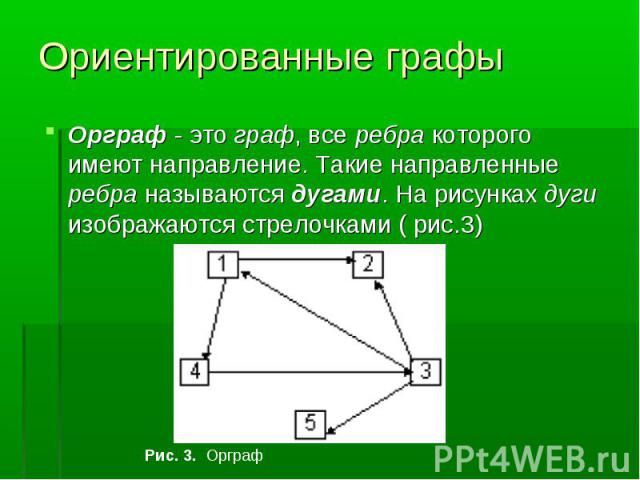
Орграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками ( рис.3)

В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу. В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу. Если в графе присутствуют и ребра, и дуги, то его называют смешанным

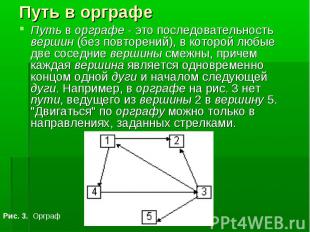
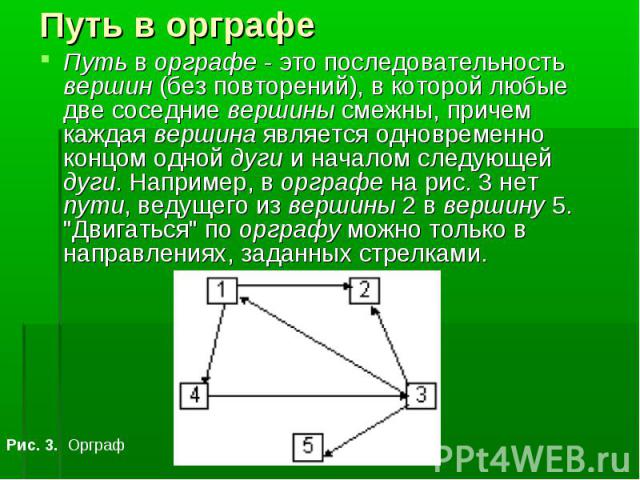
Путь в орграфе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 3 нет пути, ведущего из вершины 2 в вершину 5. "Двигаться" по орграфу можно только в направлениях, заданных стрелками. Путь в орграфе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 3 нет пути, ведущего из вершины 2 в вершину 5. "Двигаться" по орграфу можно только в направлениях, заданных стрелками.

Взвешенный (другое название: размеченный) граф (или орграф) - это граф (орграф), некоторым элементам которого (вершинам, ребрам или дугам) сопоставлены числа. Наиболее часто встречаются графы с помеченными ребрами. Числа-пометки носят различные названия: вес, длина, стоимость.

Длина пути во взвешенном (связном) графе - это сумма длин (весов) тех ребер, из которых состоит путь. Расстояние между вершинами - это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 4, равно 6. Длина пути во взвешенном (связном) графе - это сумма длин (весов) тех ребер, из которых состоит путь. Расстояние между вершинами - это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 4, равно 6.

Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования. Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.

Матрица смежности Sm - это квадратная матрица размером N x N (N - количество вершин в графе), заполненная по следующему правилу: Матрица смежности Sm - это квадратная матрица размером N x N (N - количество вершин в графе), заполненная по следующему правилу: Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = Ves(e), в противном случае Sm[u,v] = “-”.

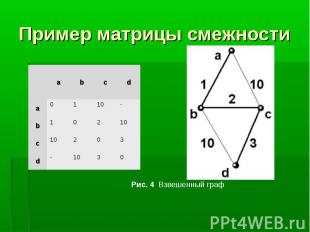
Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей). Кроме того, для "общения" с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных. Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей). Кроме того, для "общения" с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.

В одном линейном списке содержатся номера "начальных вершин", а в остальных - номера смежных вершин или указатели на эти вершины. В качестве примера приведем иерархический список, задающий орграф, изображенный на рис.3 В одном линейном списке содержатся номера "начальных вершин", а в остальных - номера смежных вершин или указатели на эти вершины. В качестве примера приведем иерархический список, задающий орграф, изображенный на рис.3

Вершина = запись Вершина = запись Номер: Число; Имя: Строка; След Вершина: указатель на Вершина; Список Дуг: Дуга; end; Дуга = запись Стоимость: Число; Конец Дуги: Вершина; След Дуга: Дуга; end; Очевидное преимущество такого способа представления графов заключается в экономичном использовании памяти. И даже небольшая избыточность данных, к которой приходится прибегать в случае неориентированного графа, задавая каждое ребро как две дуги, искупается гибкостью всей структуры, что особенно удобно при необходимости частых перестроений в процессе работы программы.

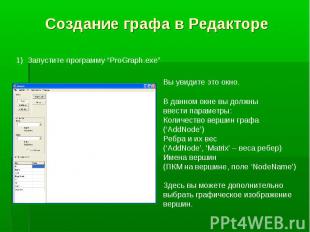
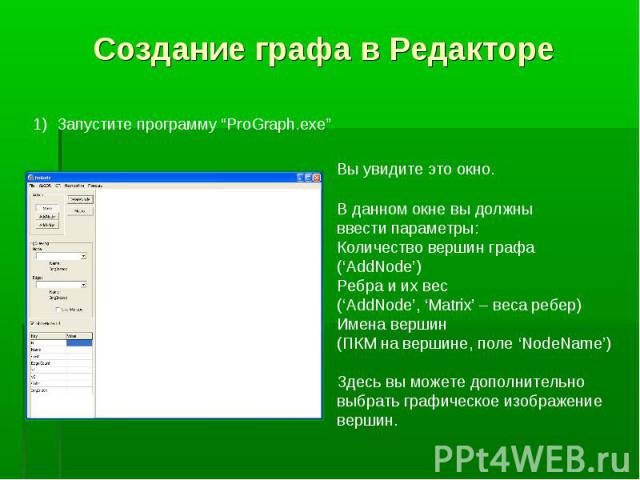
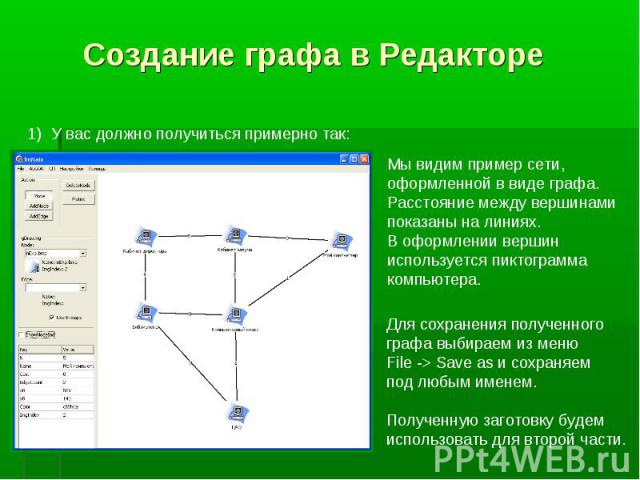
Программа “ProGraph” была специально созданна для создания графов в графической оболочке. Поддерживает возможность добавления алгоритмов на графах. Программа “ProGraph” была специально созданна для создания графов в графической оболочке. Поддерживает возможность добавления алгоритмов на графах.

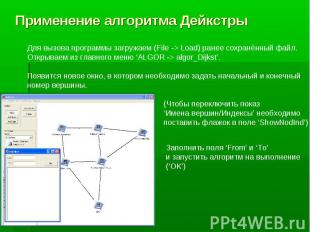
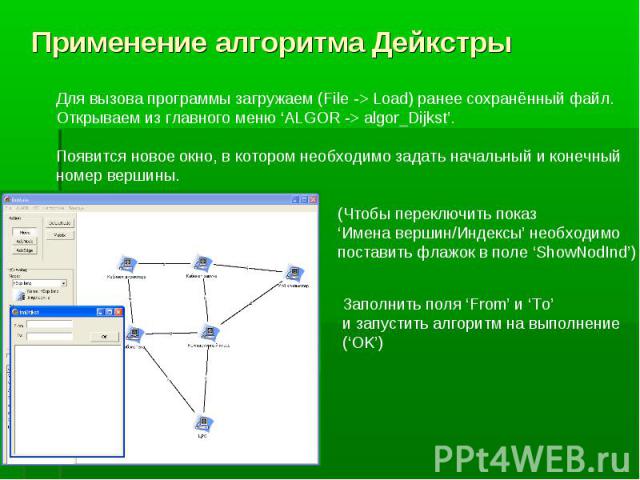
Мы рассмотрим один из основных алгоритмов поиска кратчайших путей в графе – алгоритм Дейкстры, применимый для графов с неотрицательными весами. Мы рассмотрим один из основных алгоритмов поиска кратчайших путей в графе – алгоритм Дейкстры, применимый для графов с неотрицательными весами.

Основная идея основана на простой формуле: (Dist(x) – расстояние до вершины x из исходной) Основная идея основана на простой формуле: (Dist(x) – расстояние до вершины x из исходной) Dist(Xi) = Минимум(Dist(Xi), Dist(p) +Matr(p,i))