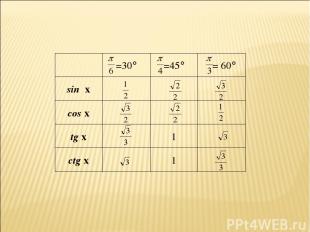
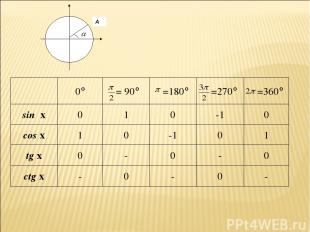
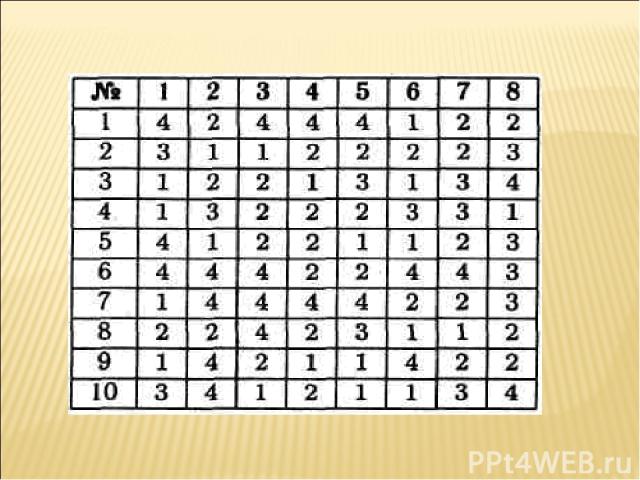
Презентация на тему: презентация методы решения тригонометрических уравнений 10 класс

МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений

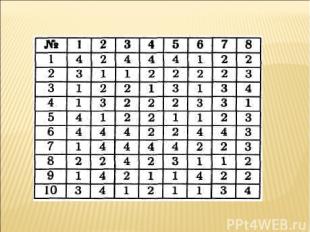
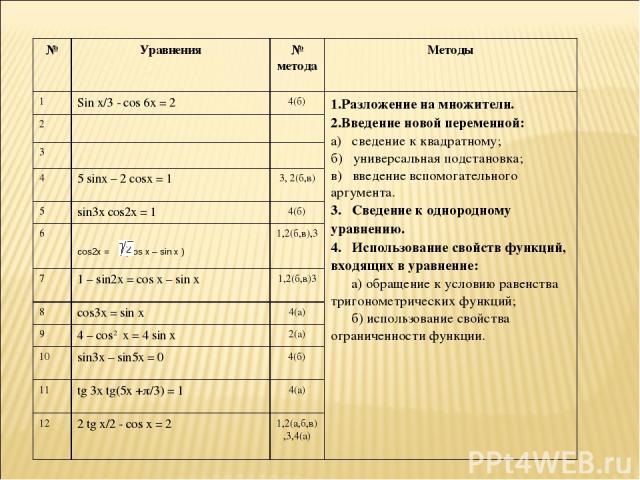
№ Уравнения № метода Методы 1 Sin x/3 - cos 6x = 2 4(б) 1.Разложение на множители. 2.Введение новой переменной: а) сведение к квадратному; б) универсальная подстановка; в) введение вспомогательного аргумента. 3. Сведение к однородному уравнению. 4. Использование свойств функций, входящих в уравнение: а) обращение к условию равенства тригонометрических функций; б) использование свойства ограниченности функции. 2 3 4 5 sinx – 2 cosx = 1 3, 2(б,в) 5 sin3x cos2x = 1 4(б) 6 cos2x = (cos x – sin x ) 1,2(б,в),3 7 1 – sin2x = cos x – sin x 1,2(б,в)3 8 cos3x = sin x 4(а) 9 4 – cos2 x = 4 sin x 2(а) 10 sin3x – sin5x = 0 4(б) 11 tg 3x tg(5x + /3) = 1 4(а) 12 2 tg x/2 - cos x = 2 1,2(а,б,в),3,4(а)

1. Какие методы решения тригонометрических уравнений вы знаете? 2. Определите и ответьте, какими методами нужно решать данные тригонометрические уравнения? а) sin 2x – cos x = 0 б) 2sin²x - 5sinx = -3 в) cos²x – sin²x = sinx – cosx г) sin2 x – 3sinx cosx + 2cos²x = 0 3.Решите простейшие тригонометрические уравнения:

Некоторые типы тригонометрических уравнений. Уравнения, сводящиеся к квадратным, относительно cos х = t, sin х = t. A sin2 x + B cosx + C = 0 A cos2 x + В sinx + C = 0 Решаются методом введения новой переменной. 2.Однородные уравнения первой и второй степени. I степени. A sinx + B cosx = 0 : cosx A tg x + B = 0 II степени. A sin2 x + B sinx cosx + A cos2 x = 0 : cos2x A tg2 x + B tgx + C = 0 Решаются методом разложения на множители и методом введения новой переменной. 3. Уравнение вида: А sinx + B cosx = C. А, В, С 0 Применимы все методы.

4. Понижение степени. А cos2x + В = C. A cos2x + B = C. Решаются методом разложения на множители. A sin2x + B = C. A sin2x + B = C. Сводятся к однородным уравнениям С = С( ).

Формулы. Универсальная подстановка. х + 2 n; Проверка обязательна! Понижение степени. = (1 + cos2x ) : 2 = (1 – cos 2x) : 2 Метод вспомогательного аргумента.

Сведение к однородному. Разложение на множители.

1.Потеря корней: делим на g(х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g(х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения. Проблемы ,возникающие при решении тригонометрических уравнений

Уравнение . Уравнение . Поделив уравнение на , получим , , При решении этой задачи обе части уравнения были поделены на . Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения корнями данного уравнения. Если , то из уравнения следует, что . Однако и не могут одновременно равняться нулю, так как они связаны равенством . Следовательно, при делении уравнения , где , , на (или ) получаем уравнение, равносильное данному.

, x = y + . Решить уравнение cos²x + sinx cosx = 0 1) Делить на cosx нельзя, так как в условии не указано , что cosx не равен нулю. Но можно утверждать, что sinx не равен нулю, так как в противном случае cosx равен 0, что невозможно , так как sin²x-cos²x =1. Значит можно разделить на sin²x. 2) Решим уравнение разложением на множители: cos²x + sinx cosx = 0, сosx(cosx + sinx ) = 0, сosx = 0 или cosx + sinx = 0, tg x=-1,

Уравнения, линейные относительно sin x и cos x а sin x + в cos x = с. Если а=в=0, а с не равно 0, то уравнение теряет смысл; Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество. Рассмотрим случаи, когда а,в,с не равны 0. Примеры: 3 sin 5x - 4 cos 5x = 2 2 sin 3x + 5 cos 3x = 8. Последнее уравнение не имеет решений, так как левая часть его не превосходит 7. Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tgх ; сведением уравнения к однородному; введением вспомогательного аргумента и другими. Решение этих уравнений существует при

Данное уравнение является уравнением вида , (1) где , , , которое можно решить другим способом. Разделим обе части этого уравнения на : . (2) Введем вспомогательный аргумент , такой, что . Такое число существует, так как . Таким образом, уравнение можно записать в виде . Последнее уравнение является простейшим тригонометрическим уравнением.

Уравнение . Используя формулы sin x = 2 sin cos , cos x = cos2 - sin2 и записывая правую часть уравнения в виде , получаем Поделив это уравнение на , получим равносильное уравнение Обозначая , получаем , откуда . 1) 2) Ответ:

4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0

4sin²x - 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2 сos²x – sin x – 1 = 0 ±П/6 +Пn; -П/2+2Пn, n Z.

Решить уравнение Здесь Поделим обе части уравнения на 5: Введем вспомогательный аргумент , такой, что , . Исходное уравнение можно записать в виде , , откуда Ответ: