Презентация на тему: Квадратичная функция и её применение при решении задач с параметрами

исследовательская работа «Квадратичная функция и её применение при решении задач с параметрами» Выполнил: Половинкин Никита, ученик 10 «а» класса

«Метод решения хорош, если с самогоначала мы можем предвидеть – и далее подтвердить это, - что, следуя этому методу, мы достигнем цели». Лейбниц, Opuscules Цель работы: показать, как использование свойств квадратичной функции, помогает при решении задач с параметрами.

Параметр – это буквенная часть, которую содержит уравнение, не считая неизвестную переменную. Буквенная часть (параметр) может скрывать целое «семейство» чисел, при подстановке которых уравнение становится верным. Решить задачу с параметрами – это значит установить, при каких значениях параметров она имеет решения, и найти эти решения (как правило, в зависимости от параметров), то есть решение подобных задач должно сопровождаться исследованием. Хотя для решения задач с параметрами не требуется никаких специальных знаний, выходящих за рамки школьной программы, необходимость проводить исследование значительно осложняет решения задач этого типа. Для достижения указанной цели нам необходимо было решить следующие задачи.Ознакомиться со свойствами квадратичной функции, в частности, с взаимным расположением корней в зависимости от значений коэффициентов.Изучить методы решения задач с параметрами, выделив те, где используются свойства квадратичной функции.Сделать подборку задач, позволяющих проиллюстрировать эти методы.Подобрать задачи для самостоятельного решения.Сделать обзор литературы по этой теме.Оформить презентацию. Выбранная тема является актуальной, т.к. задачи с параметрами данного типа встречаются на ЕГЭ и олимпиадах.Практическая значимость – данная работа может быть использована школьниками при подготовке к вступительным экзаменам, к ЕГЭ.

1 Задачи на определение числа решенийВыделяют три основных подхода к решению задач с параметрами:аналитический метод решения,графический метод с использованием координатной плоскости 1.1 Аналитический методАналитический метод является наиболее трудоемким, но, в то же время, наиболее строгим методом решения. При наличии времени можно рекомендовать его использование для подкрепления правоты полученных результатов после предварительного применения одного из графических методов и получения ответа.Характерной особенностью аналитических методов решения является использование «двойственной» природы параметра, с которым можно обращаться как с обычным числом до тех пор, пока этому не препятствует его неизвестность.

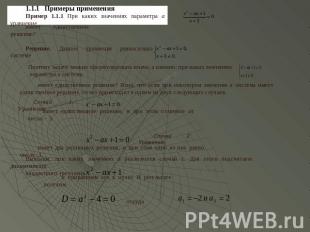
имеет единственное решение? Поэтому задачу можно сформулировать иначе, а именно: при каких значениях параметра а система имеет единственное решение? Ясно, что если при некотором значении а система имеет единственное решение, то это происходит в одном из двух следующих случаев. имеет единственное решение, и при этом отличное от числа - 3. Выясним, при каких значениях а реализуется случай 1. Для этого подсчитаем дискриминант квадратного трехчлена

Полученные значения а должны быть проверенны на предмет выполнения условия . С этой целью подставим полученные значения а в уравнение , каждое из которых отлично от числа -3. Таким образом, значения Выясним теперь, при каких значениях параметра а реализуется случай 2. Поскольку, в силу самого определения случая 2, число опять-таки требует проверки, которая должна выяснить, не является ли число двукратным корнем уравнения . Если бы это было именно так, то найденное значение , имеет еще решение . Следовательно, значения

1.2 Графический метод 1.2.1 Суть алгоритмаВ данном разделе рассматриваются задачи, при решении которых, помимо аналитических методов, применяются некоторые графические приёмы. Графический метод прост и нагляден, но пользоваться им нужно с большой аккуратностью, подкрепляя, увиденное на чертеже, необходимыми аналитическими выкладками. 1.2.2 Примеры примененияПример 1.2.1 Найти число корней уравнения Решение. Построим графики функций, стоящих в левой , мы заставляем эту прямую, оставаясь всё время горизонтальной, перемещаться вверх. Поскольку число корней исходного уравнения равно числу общих точек, которые имеют два указанных графика, то ответ непосредственно усматривается из чертежа (рис. 1). , то это горизонтальная прямая. На чертеже она изображена для случая

1.3 Координатно-параметрический метод1.3.1 Суть алгоритмаКоординатно-параметрический метод основан на нахождении множества всех точек плоскости, значения координаты х и параметра а каждой из которых удовлетворяют заданному в условиях задачи условию (соотношению). Если указанное множество точек найдено, то можно каждому допустимому значению параметра поставить в соответствие координаты х точек этого множества, дающие искомое решение задачи, или указать те значения параметра, при которых задача не имеет решения. Пример 1.3.1 Найти все значения параметра ф множество всех точек Решение. На координатно-параметрической плоскости , значения координаты и параметра каждой из которых удовлетворяют данному уравнению, представляет собой параболу – график функции

2 Теорема Виета2.1 Основные теоретические сведения Известно, что если х1 и х2 – корни квадратного трехчлена (1)Равенство (1) дает возможность установить следующие соотношения между корнями и коэффициентами квадратного уравнения: Утверждение, выраженное соотношениями (2), носит название теоремы Виета. Теорема Виета имеет очень большое практическое значение и часто используется при решении различных задач, в том числе и задач с параметрами. С помощью этой теоремы можно легко устанавливать знаки корней (или формулировать условия, определяющие заданные знаки корней), вычислять по коэффициентам уравнения некоторые выражения, зависящие от корней уравнения, не вычисляя самих корней, решать системы вида:

и теорему Виета, получаем систему: – корни уравнения. Тогда, учитывая условие

3 Расположение данного числа относительно корней квадратного трехчлена3.1 Основные теоретические сведенияИсследования знака дискриминанта позволяют установить, действительны или комплексны корни квадратного трехчлена. Однако для целого ряда задач этого оказывается недостаточно и требуется еще установить, как расположены на числовой оси действительные корни квадратного трехчлена относительно каких-либо фиксированных точек числовой оси. Это удается сделать, используя следующую серию теорем. Теорема 1. Для того чтобы оба корня квадратного трехчлена были действительными и оба больше, чем число Теорема 2. Для того чтобы оба корня квадратного трехчлена были действительными и один из них был меньше, чем число (т.е. были расположены на числовой оси по разные стороны от точки

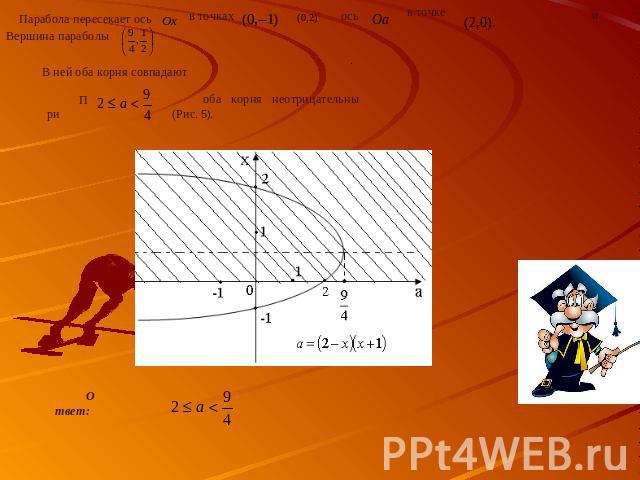
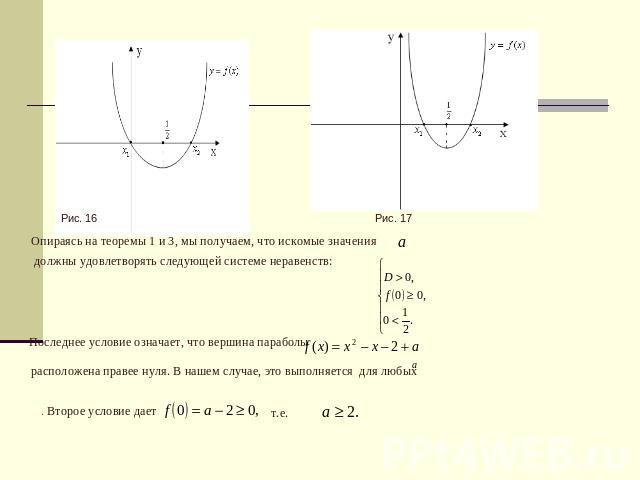
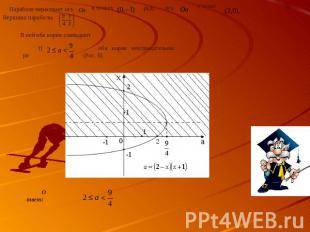
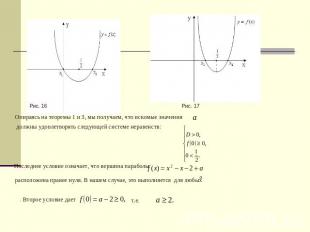
Теорема 3. Для того чтобы оба корня квадратного трехчлена были действительными и оба меньше, чем число (т.е. были расположены на числовой оси левее, чем точка ), необходимо и достаточно, чтобы 3.2 Примеры применения данной теории Пример 3.2.1 Найти все значения , при которых уравнение имеет два различных неотрицательных решения. Решение. Исходная задача эквивалентна следующей: найти все значения а, при которых число нуль расположено не правее двух различных корней данного уравнения. и возможна одна из следующих ситуаций: (см. рис. 16 и рис.17).

Опираясь на теоремы 1 и 3, мы получаем, что искомые значения должны удовлетворять следующей системе неравенств: Последнее условие означает, что вершина параболы расположена правее нуля. В нашем случае, это выполняется для любых . Второе условие дает

Чтобы это уравнение имело два действительных различных корня, достаточно, чтобы его дискриминант был положителен, т.е. чтобы было Итак, для всех значений из промежутка число нуль расположено не правее двух различных корней данного уравнения. Указанный промежуток дает решение поставленной задачи.

Пример 4.3 (С-5) Пусть А – множество тех значений параметра Найдите множество значений, которое при этих условиях принимает величина Решение. Уравнение имеет два различных действительных корня, если дискриминант квадратного трехчлена положителен, т. е. , что дает нам первое условие: По теореме Виета , запишется в виде неравенства: Учитывая первое условие, получаем, что Рассмотрим теперь величину

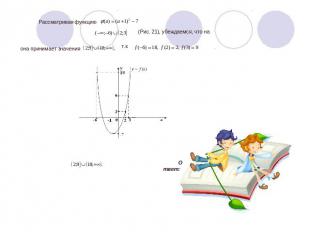
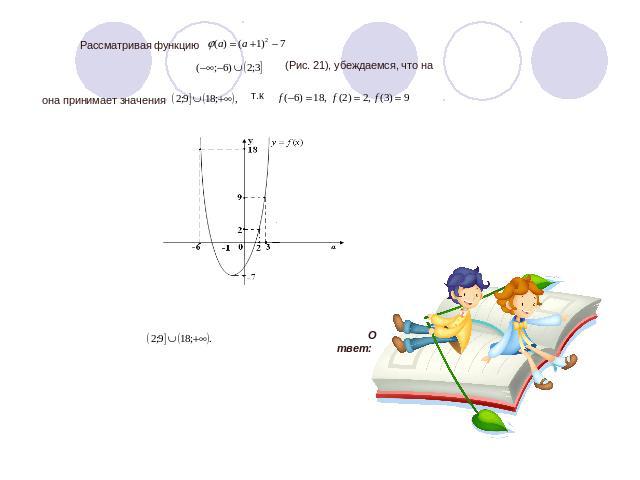
(Рис. 21), убеждаемся, что на она принимает значения

Рассмотрев наиболее распространенные методы решения подобных задач: аналитический, графический, координатно-параметрический и теорему Виета, мы пришли к выводу, что каждый из них является эффективным для своего определенного круга задач. Более наглядным является координатно-параметрический метод, так как позволяет явно увидеть, при каких значениях параметра выполняются требуемые условия.Выбранная тема является актуальной, т.к. задачи с параметрами данного типа встречаются на ЕГЭ и олимпиадах. В школьных учебниках же практически нет заданий на эту тему. Однако овладение методикой их решения нам кажется необходимым: оно существенно повышает уровень логической подготовки, позволяет чуть по-новому, как бы изнутри, взглянуть на такие «банальные» функциональные зависимости, подробно анализируемые школьной программой, как, к примеру, линейные или квадратные многочлены. Практическая значимость – данная работа может быть использована школьниками при подготовке к вступительным экзаменам, к ЕГЭ.