Презентация на тему: Квадратичная функция: просто о сложном

Муниципальное общеобразовательное учреждениеВязьма-Брянская средняя общеобразовательная школаКвадратичная функция:просто о сложном Выполнила: ученица 9 классаКлименкова Ульяна, Руководитель: учитель математикиХрущенко Валентина Николаевна

ОГЛАВЛЕНИЕΙ. Введение.ΙΙ. Основная часть.1.Определение.2. Функция y = ax², её свойства и график.2.1. Свойства функции y = ax² при а>0. 2.2. Свойства функции y = ax² при а<0.3. Преобразование графиков функции y = a(x – m)² + n.3.1. Растяжение.3.2. Параллельный перенос по оси Ох.3.3. Параллельный перенос по оси Оy.3.4. Построение графика функции y = a(x – m)² + n.3.5 Построение графика по трем точкам.4.Исследование квадратичной функции.4.1. Исследование корней квадратного трехчлена.4.2. Расположение корней квадратичной функции у = ах² + вх +с .4.3.Различные способы решения квадратных уравнений.5.Решение различных задач повышенной сложности с помощью квадратичной функции.6.Решение задач из ЕГЭ 9 класса с помощью квадратичной функции.ΙΙΙ. Заключение.ΙV. Список литературы.

ВВЕДЕНИЕКвадратичная функция является одной из первых, с которой мы познакомились в процессе изучения курса алгебры. С одной стороны – эта функция простая, но с другой – она интересна и обширна. После линейной функции квадратичная – простейшая и важнейшая элементарная функция. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростью V0 , находится в момент времени t на расстоянии от земной поверхности (g – ускорение); количество тепла Q, выделяемого при прохождении тока в проводнике с сопротивлением R, выражается через силу тока формулой Задачи с параметрами на квадратичную функцию и задачи, сводящиеся к квадратичным функциям, очень популярны на экзаменах в вузы, ЕГЭ, школьных олимпиадах разного уровня. Квадратичная функция является одной из главных школьной математики для которой построена полная теория и доказаны все свойства, а от учащегося требуется четкое понимание и знание всех этих свойств. При этом задач на квадратичную функцию очень много – от простых, непосредственно вытекающих из формул и теории, до сложных, требующих всестороннего анализа и глубокого понимания свойств функции. Условия на существование корней, число корней, их значений, поведение и свойства графиков функции можно сформулировать в терминах соотношений между коэффициентами и условий на коэффициенты.

По знакам коэффициентов можно однозначно восстановить эскиз графика функции. Знак выражения определяет существование и число корней. Важно понимать, как влияют коэффициенты квадратичной функции, их знаки, соотношения между ними на свойства функции и ее графика. Большое практическое значение при решении задач на квадратичную функцию имеет наличие однозначного соответствия между алгебраическим описанием и геометрической интерпретацией задачи – графическим изображением и положением эскиза графика функции на координатной плоскости. С одной стороны, от учащихся требуется свободное владение свойствами квадратичной функции и умение построить соответствующую графическую интерпретацию, с другой - геометрическая интерпретация помогает проверить логическую правильность и непротиворечивость теоретических рассуждений. Задачи на расположение корней квадратичной функции и сводящиеся к ним – одни из самых популярных в задачах с параметрами. Эта тема позволит углубить наши знания о квадратичной функции и повысить интерес учащихся к ней.Цель моей работы – исследовать квадратичную функцию, осуществить её полный анализ и применить к решению задач из ЕГЭ и из другой литературы различного уровня сложности.

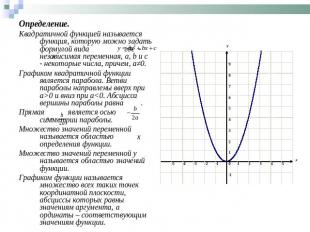
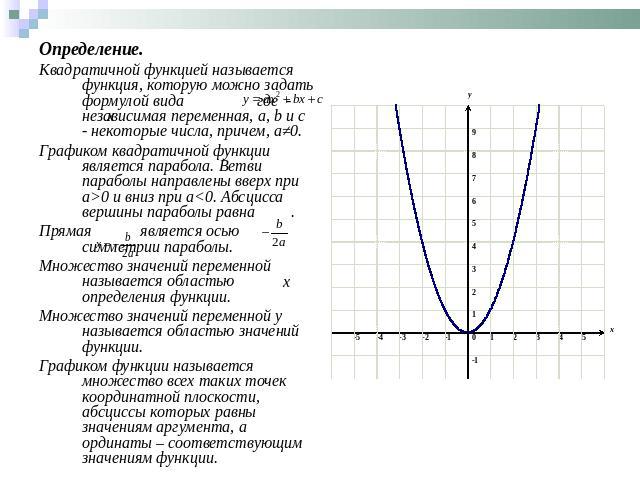
Определение.Квадратичной функцией называется функция, которую можно задать формулой вида где - независимая переменная, а, b и с - некоторые числа, причем, а≠0.Графиком квадратичной функции является парабола. Ветви параболы направлены вверх при а>0 и вниз при а<0. Абсцисса вершины параболы равна . Прямая является осью симметрии параболы.Множество значений переменной называется областью определения функции.Множество значений переменной y называется областью значений функции.Графиком функции называется множество всех таких точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

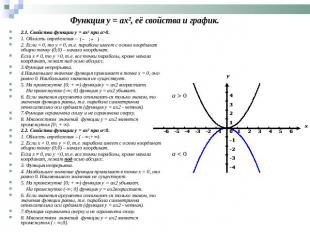
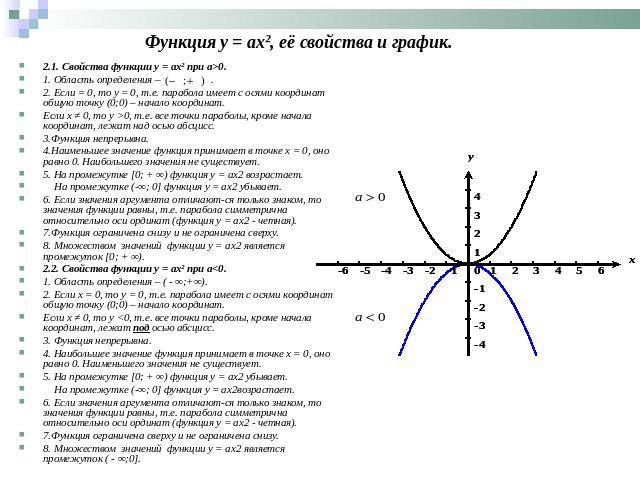
2.1. Свойства функции y = ax² при а>0.1. Область определения – .2. Если = 0, то y = 0, т.е. парабола имеет с осями координат общую точку (0;0) – начало координат.Если х ≠ 0, то y >0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.3.Функция непрерывна.4.Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.5. На промежутке [0; + ∞) функция у = aх2 возрастает. На промежутке (-∞; 0] функция у = aх2 убывает.6. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = aх2 - четная).7.Функция ограничена снизу и не ограничена сверху.8. Множеством  значений  функции у = aх2 является промежуток [0; + ∞).2.2. Свойства функции y = ax² при а<0.1. Область определения – ( - ∞;+∞).2. Если х = 0, то y = 0, т.е. парабола имеет с осями координат общую точку (0;0) – начало координат.Если х ≠ 0, то y <0, т.е. все точки параболы, кроме начала координат, лежат под осью абсцисс.3. Функция непрерывна.4. Наибольшее значение функция принимает в точке х = 0, оно равно 0. Наименьшего значения не существует.5. На промежутке [0; + ∞) функция у = aх2 убывает. На промежутке (-∞; 0] функция у = aх2возрастает.6. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. парабола симметрична относительно оси ординат (функция у = aх2 - четная).7.Функция ограничена сверху и не ограничена снизу.8. Множеством  значений  функции у = aх2 является промежуток ( - ∞;0].

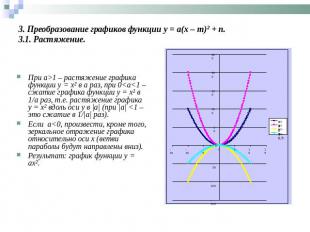
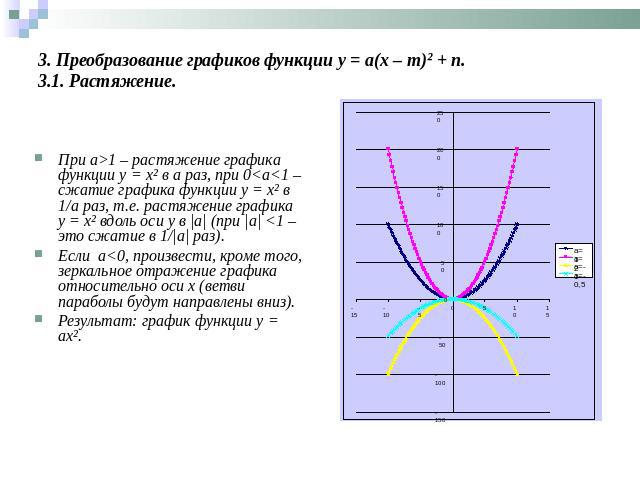
3. Преобразование графиков функции y = a(x – m)² + n.3.1. Растяжение. При а>1 – растяжение графика функции y = x² в а раз, при 0<а<1 – сжатие графика функции y = x² в 1/a раз, т.е. растяжение графика y = x² вдоль оси y в |а| (при |а| <1 – это сжатие в 1/|а| раз). Если а<0, произвести, кроме того, зеркальное отражение графика относительно оси х (ветви параболы будут направлены вниз).Результат: график функции y = ax².

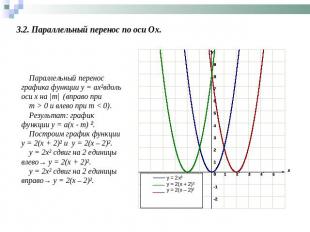
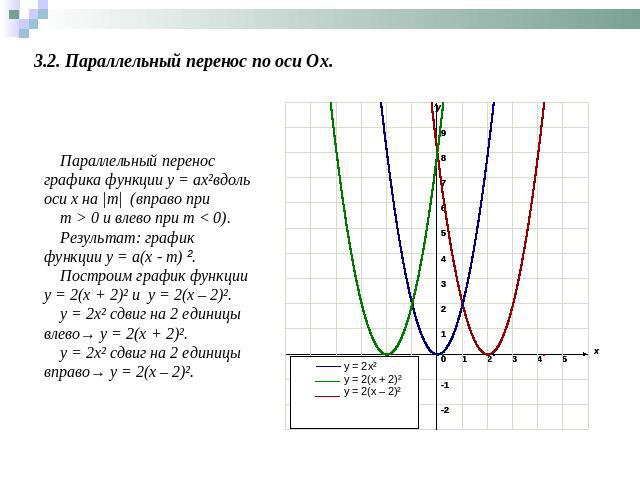
3.2. Параллельный перенос по оси Ох. Параллельный перенос графика функции у = ах²вдоль оси х на |m|  (вправо при m > 0 и влево при т < 0).Результат: график функции у = а(х - т) ².Построим график функции y = 2(x + 2)² и y = 2(x – 2)².y = 2x² сдвиг на 2 единицы влево→ y = 2(x + 2)².y = 2x² сдвиг на 2 единицы вправо→ y = 2(x – 2)².

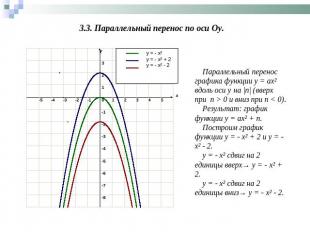
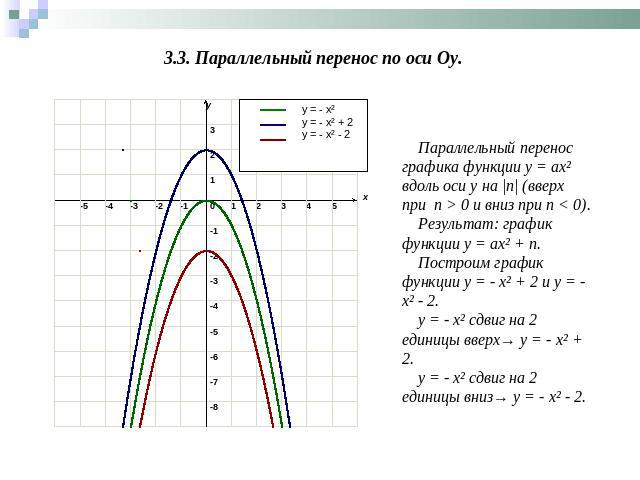
3.3. Параллельный перенос по оси Оy. Параллельный перенос графика функции у = ах² вдоль оси у на |n| (вверх при п > 0 и вниз при п < 0).Результат: график функции у = ах² + n.Построим график функции y = - x² + 2 и y = - x² - 2.y = - x² сдвиг на 2 единицы вверх→ y = - x² + 2.y = - x² сдвиг на 2 единицы вниз→ y = - x² - 2.

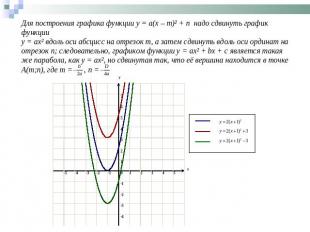
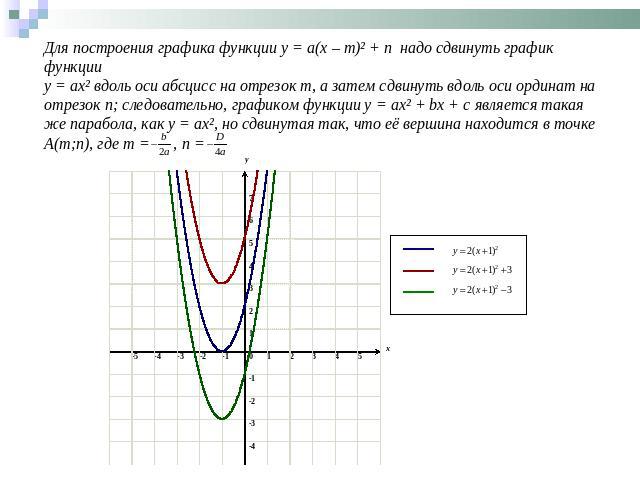
Для построения графика функции y = a(x – m)² + n надо сдвинуть график функции y = ax² вдоль оси абсцисс на отрезок m, а затем сдвинуть вдоль оси ординат на отрезок n; следовательно, графиком функции y = ax² + bx + c является такая же парабола, как у = ах², но сдвинутая так, что её вершина находится в точке А(m;n), где m = , n =

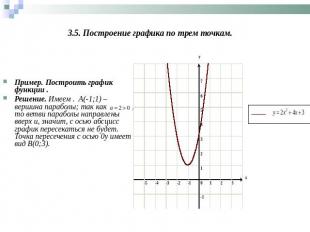
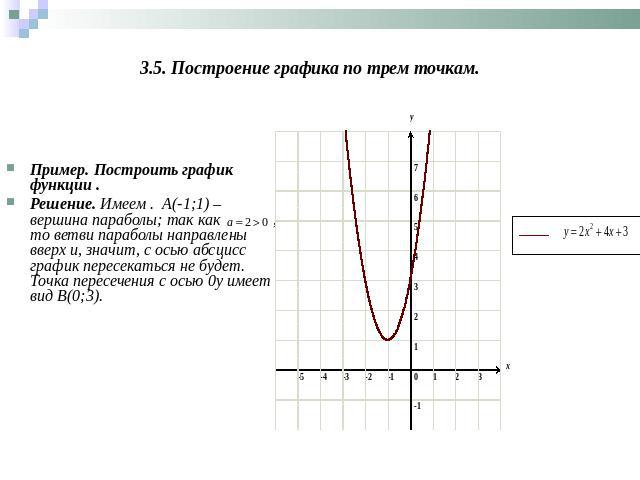
3.5. Построение графика по трем точкам. Пример. Построить график функции .Решение. Имеем . А(-1;1) – вершина параболы; так как , то ветви параболы направлены вверх и, значит, с осью абсцисс график пересекаться не будет. Точка пересечения с осью 0y имеет вид В(0;3).

4.Исследование квадратичной функции.4.1. Исследование корней квадратного трехчлена. Свойства функции и вид ее графика определяются, в основном, значениями коэффициента а и дискриминанта , что отражено в таблице.

4.2. Расположение корней квадратичной функции . Если дискриминант квадратного уравнения является полным квадратом, то лучше найти корни уравнения и дальше работать с этими корнями. Если дискриминант квадратного уравнения не является полным квадратом, то корни уравнения лучше не находить, а нужные ограничения составить на основе следующих теорем.

4.3.Различные способы решения квадратных уравнений.

5.Решение различных задач повышенной сложности с помощью квадратичной функции.

6.Решение задач из ЕГЭ 9 класса с помощью квадратичной функции.

Меня заинтересовала тема «Квадратичная функция», и я углубила свои знания о ней. Эта тема позволила мне расширить мое представление о функции и ее свойствах. С помощью изучения квадратичной функции я узнала, что существуют различные способы построения графиков и попробовала решать задачи к ЕГЭ и повышенного уровня сложности. Добиваясь поставленной цели, мы решили следующие задачи: применение практических навыков при решении задач, требующих комплексного применения знаний, полученных в ходе изучения различных учебных предметов.Проработанный и изученный мною материал формирует становление профессиональных интересов, целостное, единое представление об окружающем мире, о взаимообусловленности явлений и процессов, а также общности законов, действующих в природе. Мы встречаемся с квадратичной функцией не только при решении задач и построении графиков, но и в окружающем мире.

Кожухов С.К., Кожухова С.А. Уравнения и неравенства с параметром. – Орел: ОИУУ, 2000. - 92с. Математика: Лекции, задачи, решения: Учебное пособие/В.Г.Болтянский, Ю.В.Сидоров, М.И.Шабунин и другие; Худ. А.Шуплецов. – Мн.: ООО «Попурри», 1996. – 640с.: ил.Галицкий М.Л. и другие. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся школ и классов с углубленным изучением математики/М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич. – 2-е издание. – М.: Просвещение, 1994. – 271с.: ил.Энциклопедический словарь юного математика/сост. э 68 А.П.Савин. – М.: Педагогика, 1985. – 352с., ил.Мордкович А.Г. Алгебра. 8 класс: В двух частях. Ч.1: Учебник для общеобразовательных учреждений. – 8-е издание. – М.: Мнемозина, 2006. – 223с.: ил.Мордкович А.Г. Алгебра. 8 класс: В двух частях. Ч.2: задачник для общеобразовательных учреждений/ А.Г.Мордкович, Т.Н.Мишустина, Е.Е.Тульчинслая. – 8-е издание. – М.: Мнемозина, 2006. – 239с.: ил.Алгебра: сборник заданий для подготовки к итоговой аттестации в 9 классе./Л.В.Кузнецова, С.Б.Суворова, Е.А.Бунимович и другие. – 2-е издание. – М.: Просвещение, 2007. – 191с.: ил. – (Итоговая аттестация).