Презентация на тему: Графики квадратичной функции

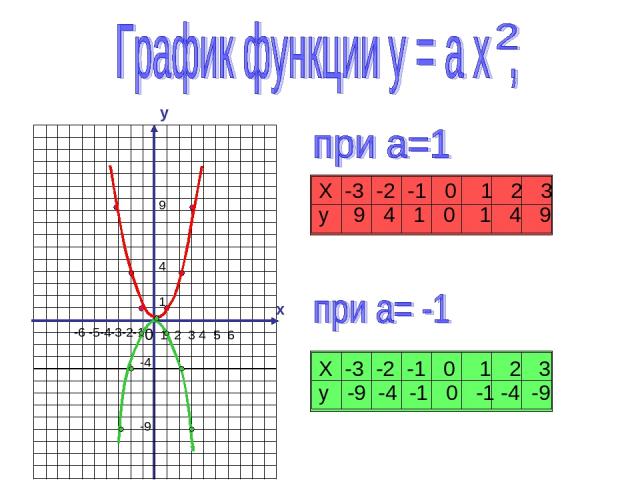
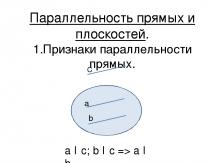
Квадратичная функция, ее график и свойства

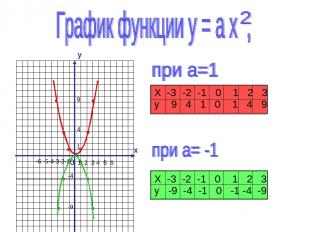
y x 0 1 2 3 4 5 6 -6 -5-4-3-2-1 1 4 9 -9 -4

Преобразование графика квадратичной функции

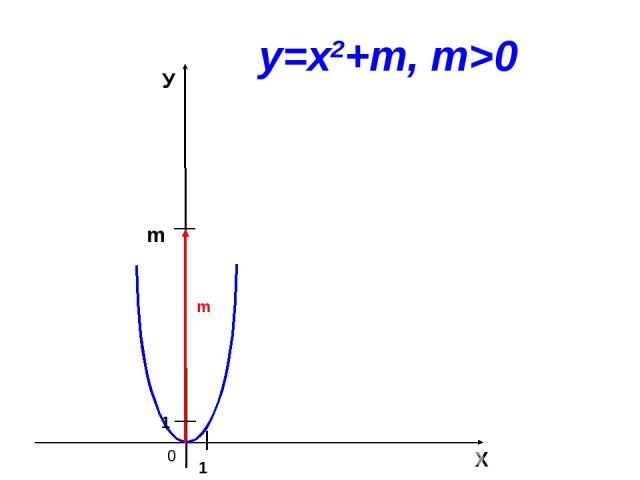
Построение графиков функций у=х2 и у=х2+m.

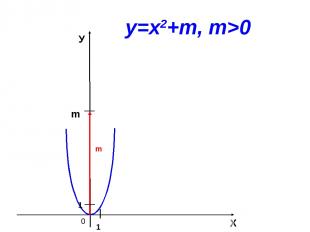
0 m Х У 1 1 у=х2+m, m>0

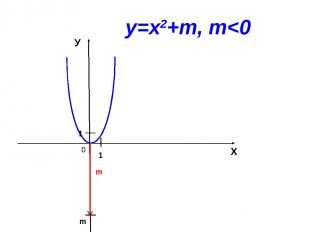
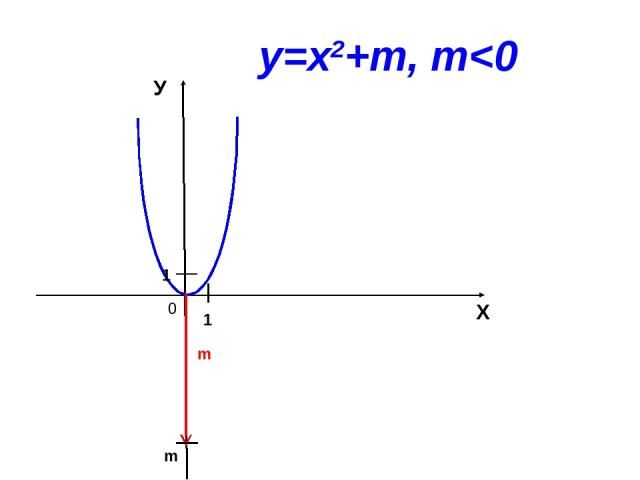
0 Х У 1 1 m у=х2+m, m

Постройте в одной координатной плоскости графики функций:

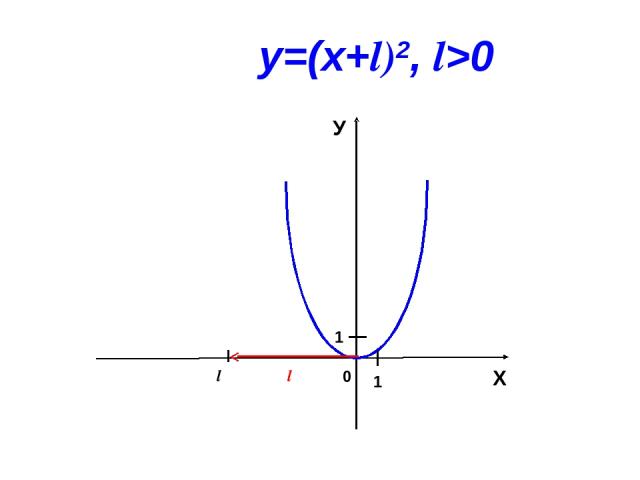
Построение графиков функций у=х2 и у=(х+l)2.

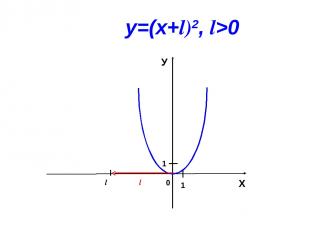
0 l Х У 1 1 у=(х+l)2, l>0

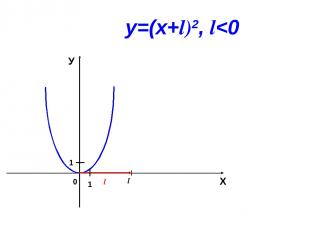
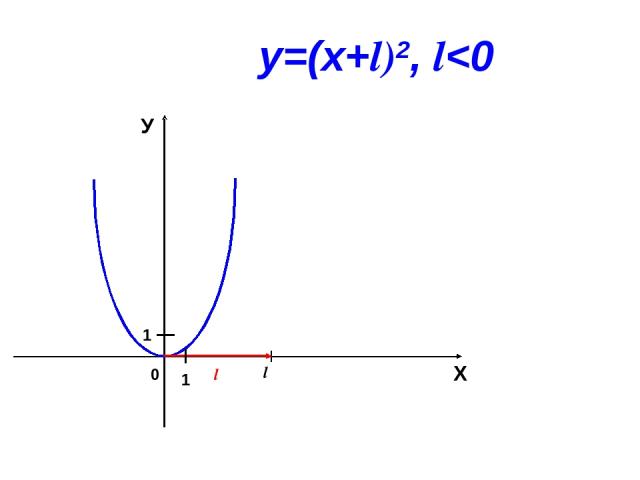
0 l Х У 1 1 у=(х+l)2, l

Постройте в одной координатной плоскости графики функций:

Найти координаты вершины параболы: У=2(х-4)² +5 У=-6(х-1)² У = -х²+12 У= х²+4 У= (х+7)² - 9 У=6 х² (4;5) (1;0) (0;12) (0;4) (-7;-9) (0;0)

График квадратичной функции, его свойства

Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х - независимая переменная, a, b и с -некоторые числа (причём а≠0). Например: у = 5х²+6х+3, у = -7х²+8х-2, у = 0,8х²+5, у = ¾х²-8х, у = -12х² квадратичные функции

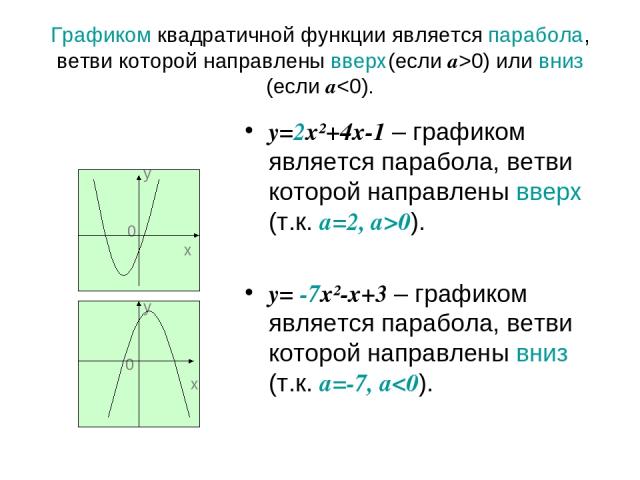
Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а0). у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а

Определить координату вершины параболы по формулам: Отметить эту точку на координатной плоскости. Через вершину параболы начертить ось симметрии параболы Найти нули функции и 0тметить их на числовой прямой Найти координаты двух дополнительных точек и симметричных им Провести кривую параболы. Алгоритм решения

Постройте график функции у=2х²+4х-6, опишите его свойства

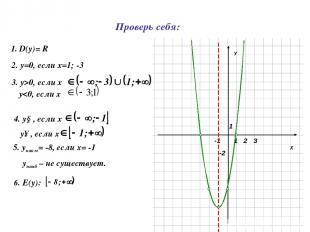
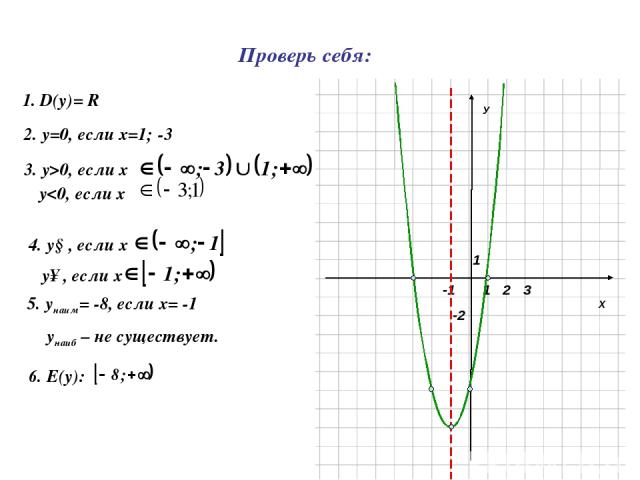
Х У 1 1 -2 2 3 -1 1. D(y)= R 2. у=0, если х=1; -3 3. у>0, если х 4. у↓, если х у↑, если х 5. унаим= -8, если х= -1 унаиб – не существует. 6. Е(y): Проверь себя: у

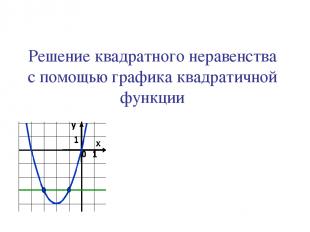
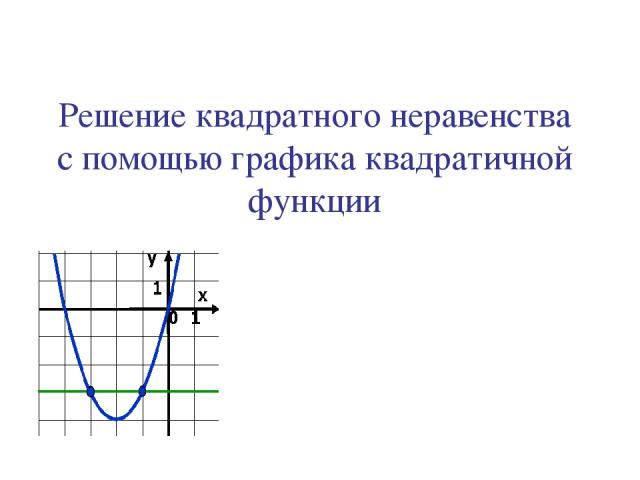
Решение квадратного неравенства с помощью графика квадратичной функции

Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая- нуль, называется неравенством второй степени. Все квадратные неравенства могут быть приведены к одному из следующих видов: 1) ах2+bx+c>0; 2) ах2+bx+c

Какие из неравенств вы бы назвали неравенствами второй степени: 1) 6х 2-13х>0; 2) x 2-3x-14>0; 3) (5+x)(x-4)>7; 4) ; 5) 6) 8x2 >0; 7) (x-5)2 -25>0;

Какие из чисел являются решениями неравенства? 1 -3 0 -1 5 -4 -2 0,5 ? ? ? ? ? ? ? ?

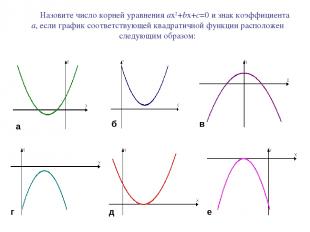
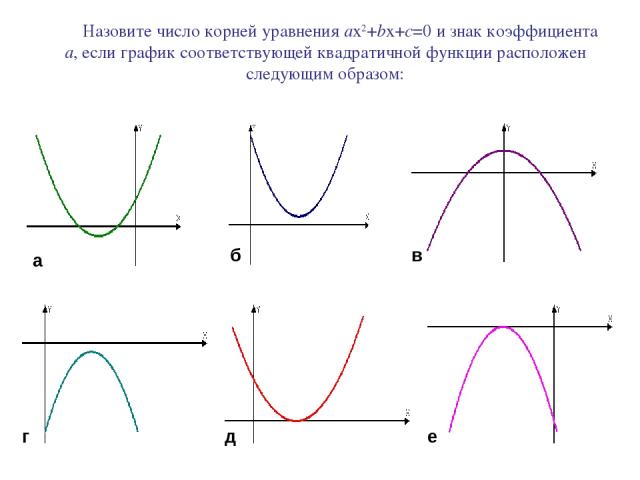
Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента а, если график соответствующей квадратичной функции расположен следующим образом: е а б в г д

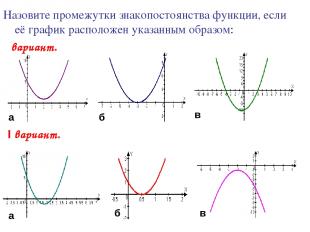
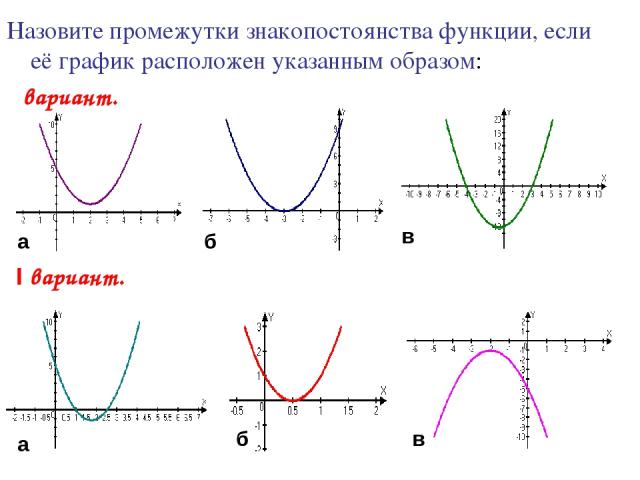
Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант. ΙІ вариант. в б а а в б

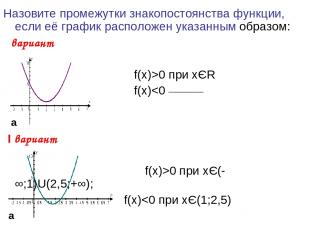
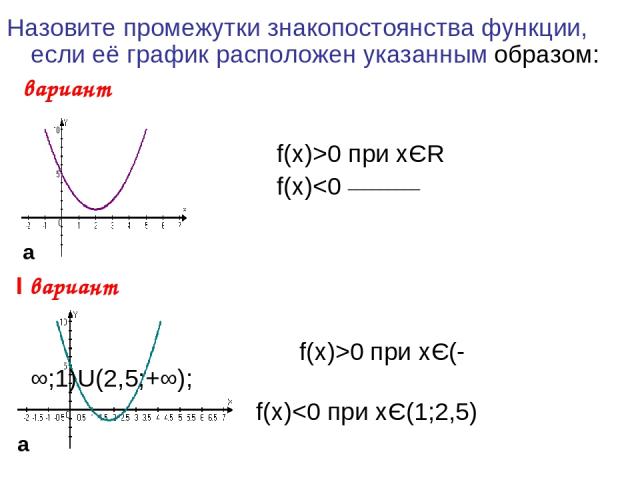
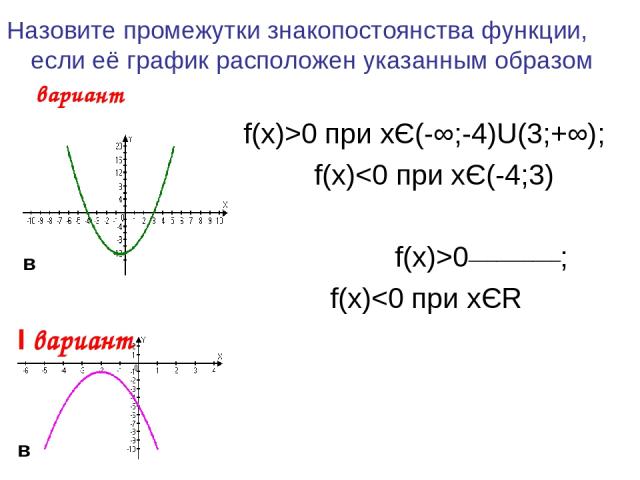
Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант f(x)>0 при xЄR f(x)0 при xЄ(-∞;1)U(2,5;+∞); f(x)

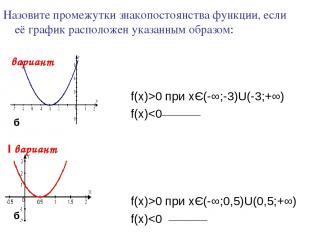
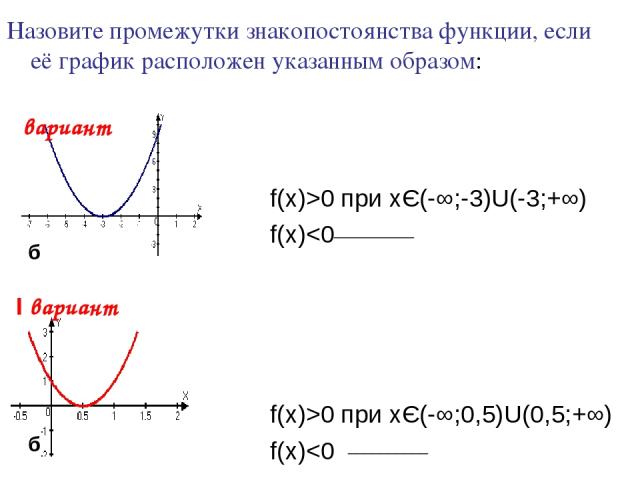
Назовите промежутки знакопостоянства функции, если её график расположен указанным образом: Ι вариант f(x)>0 при xЄ(-∞;-3)U(-3;+∞) f(x)0 при xЄ(-∞;0,5)U(0,5;+∞) f(x)

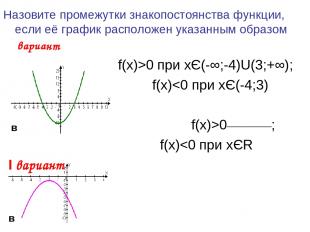
Назовите промежутки знакопостоянства функции, если её график расположен указанным образом Ι вариант f(x)>0 при xЄ(-∞;-4)U(3;+∞); f(x)0__________; f(x)

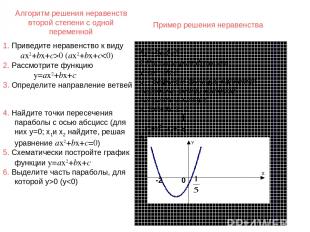
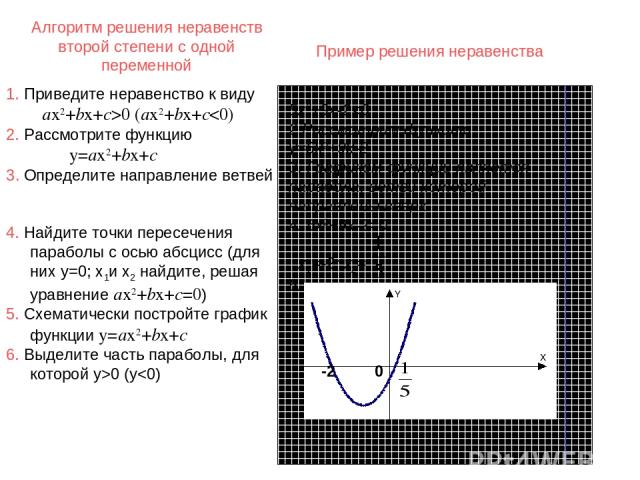
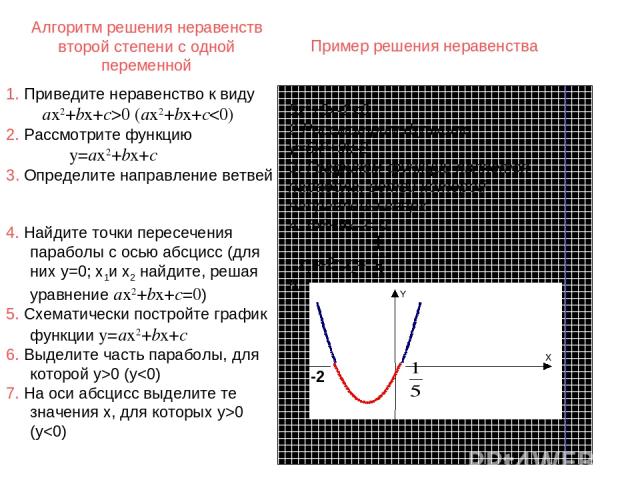
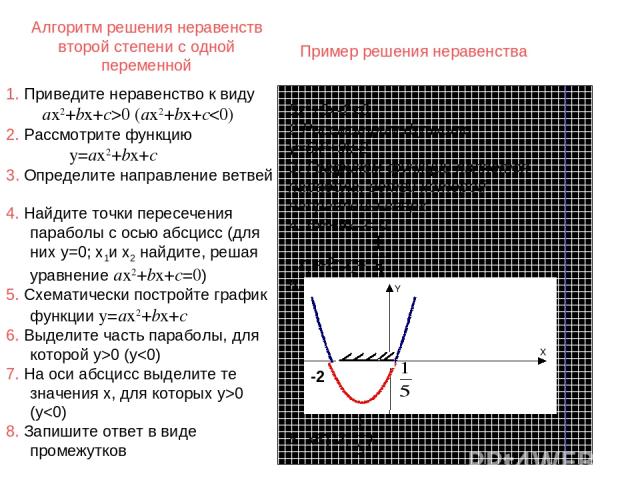
Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-20 (ax2+bx+c0 (y

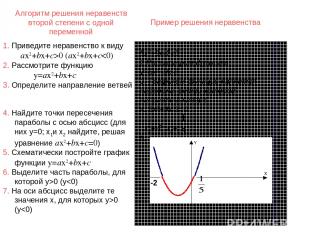
Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-20 (ax2+bx+c0 (y0 (y

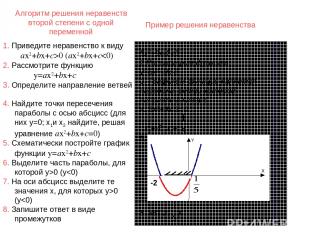
Алгоритм решения неравенств второй степени с одной переменной 5х2+9х-20 (ax2+bx+c0 (y0 (y

В таблице 1 найдите верное решение неравенства 1, в таблице 2 - решение неравенства 2: 1. 2. Таблица 1 а в с d а в с d Таблица 2

В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2. Таблица 1 а в с d а в с d Таблица 2

В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2. Таблица 1 а в с d а в с d Таблица 2

В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2: 1. 2. Таблица 1 а в с d а в с d Таблица 2

Итог урока При решении данных заданий нам удалось систематизировать знания о применении квадратичной функции. Математика- это содержательное, увлекательное и доступное поле деятельности, дающее ученику богатую пищу для ума. Свойства квадратичной функции лежат в основе решения квадратных неравенств. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростьюv0, находится в момент времени t на расстоянии s(t)=-q\2t2+v0t от земной поверхности (здесь q- ускорение силы тяжести); количество тепла Q, выделяемое при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой Q=RI2. Знания свойств квадратичной функции позволяют рассчитать дальность полета тела, брошенного вертикально вверх или под некоторым углом. Этим пользуются в оборонной промышленности.

Незаконченное предложение Задание: закончить одно из трех предложений, которое больше других соответствует вашему состоянию. “Выполнять задания и решать задачи мне трудно, так как …” “Выполнять задания и решать задачи мне легко, так как …” “Выполнять задания и решать задачи для меня занятие приятное и интересное, потому что…”

Домашнее задание Учебник №142; №190