Презентация на тему: Применение производной для исследования функции

Применение производной для исследования функции Урок в 10 классе Автор: учитель математики МБОУ г. Мурманска СОШ № 31 Сидоровой А.В.

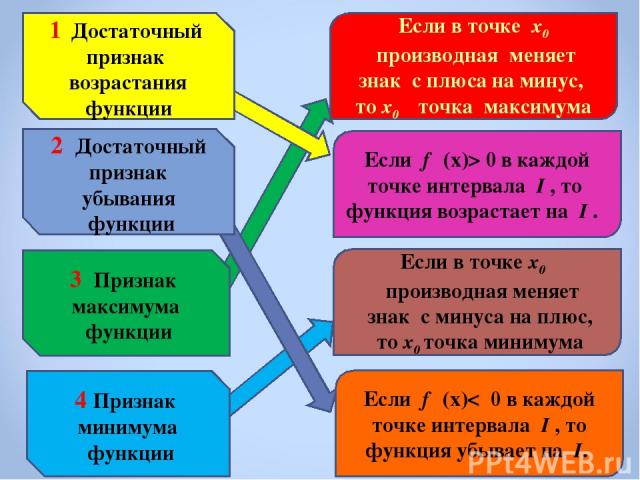
1 Достаточный признак возрастания функции 2 Достаточный признак убывания функции 3 Признак максимума функции 4 Признак минимума функции Если в точке х0 производная меняет знак с плюса на минус, то х0 точка максимума Если f ′(х)> 0 в каждой точке интервала I , то функция возрастает на I . Если в точке х0 производная меняет знак с минуса на плюс, то х0 точка минимума Если f ′(х)< 0 в каждой точке интервала I , то функция убывает на I.

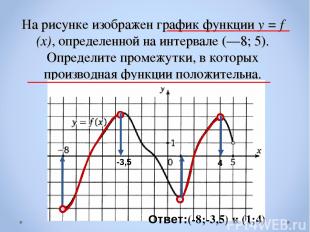
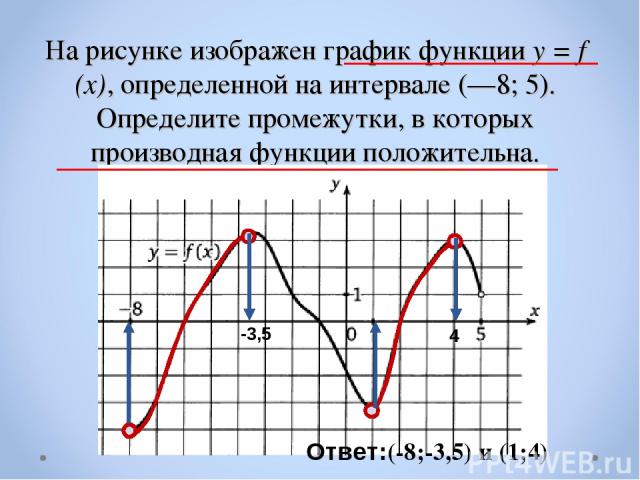
На рисунке изображен график функции y = f (x), определенной на интервале (—8; 5). Определите промежутки, в которых производная функции положительна. Ответ:(-8;-3,5) и (1;4) -3,5 4

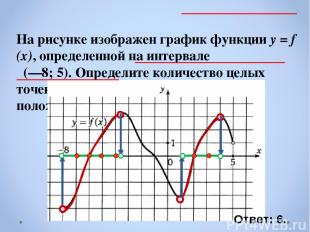
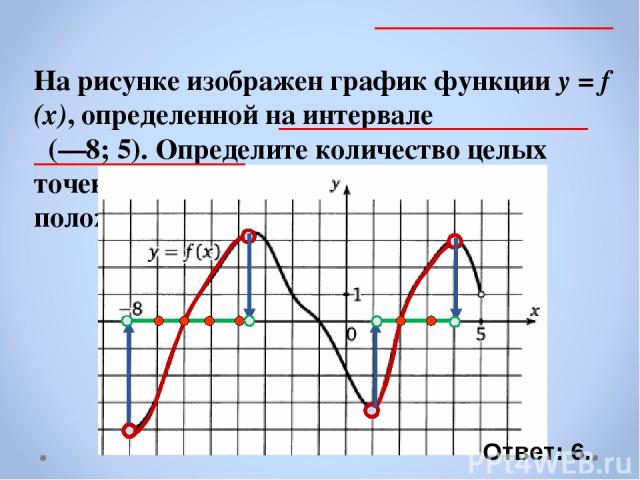
На рисунке изображен график функции y = f (x), определенной на интервале (—8; 5). Определите количество целых точек, в которых производная функции положительна. Ответ: 6.

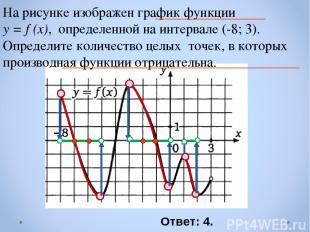
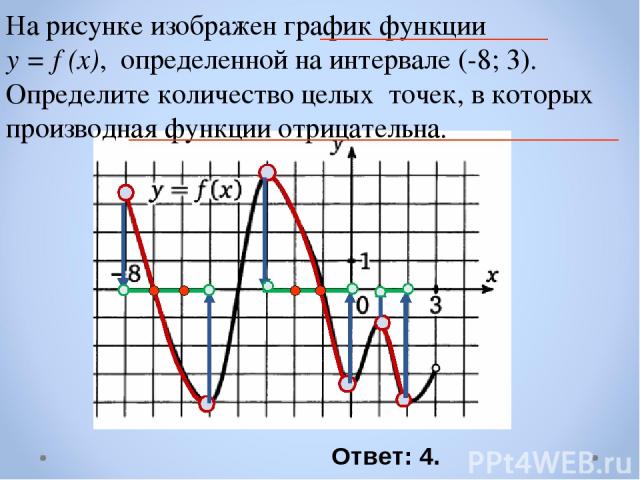
На рисунке изображен график функции y = f (x), определенной на интервале (-8; 3). Определите количество целых точек, в которых производная функции отрицательна. Ответ: 4.

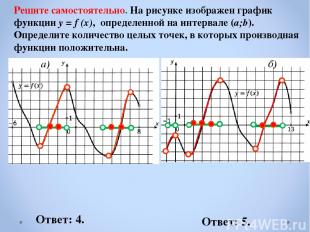
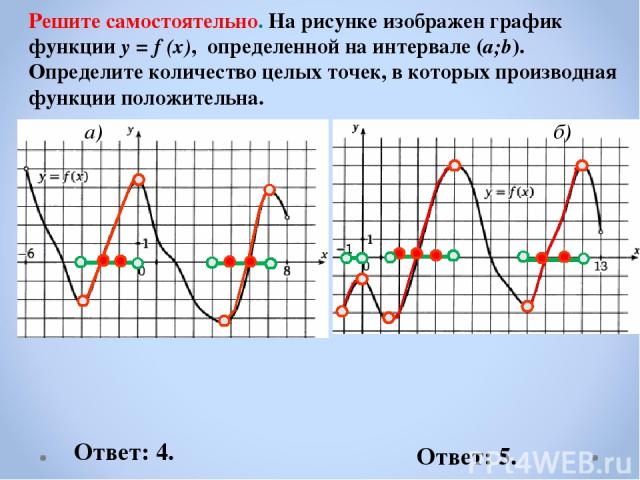
Решите самостоятельно. На рисунке изображен график функции y = f (x), определенной на интервале (a;b). Определите количество целых точек, в которых производная функции положительна. a) б) Ответ: 4. Ответ: 5.

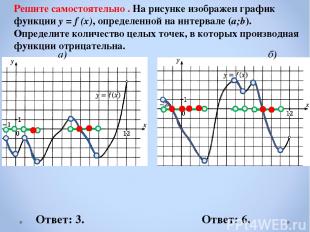
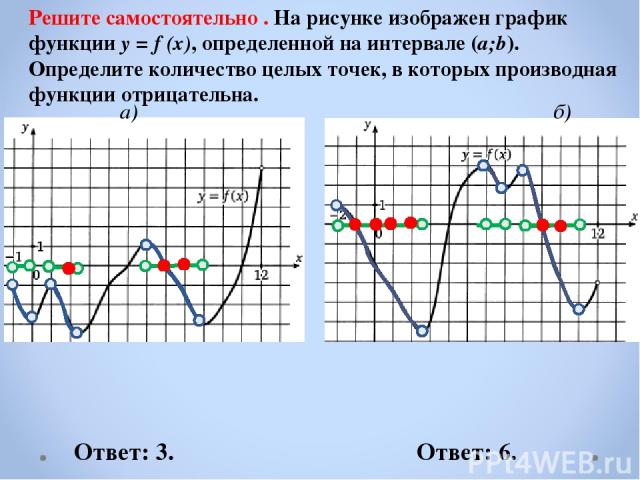
Решите самостоятельно . На рисунке изображен график функции y = f (x), определенной на интервале (a;b). Определите количество целых точек, в которых производная функции отрицательна. a) б) Ответ: 3. Ответ: 6.

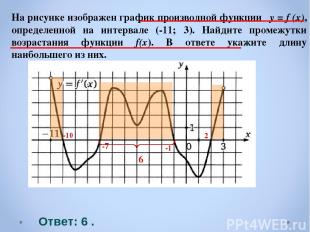
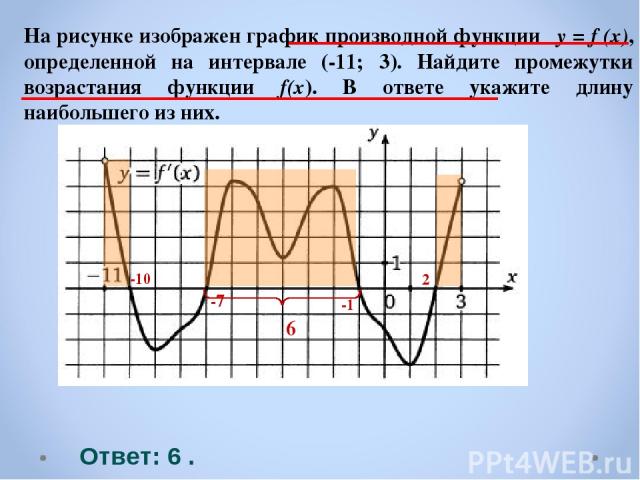
На рисунке изображен график производной функции y = f (x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них. Ответ: 6 . -10 -7 -1 2 6

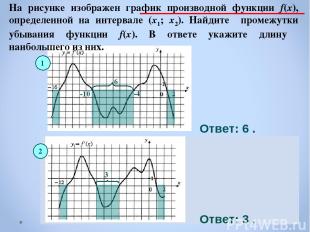
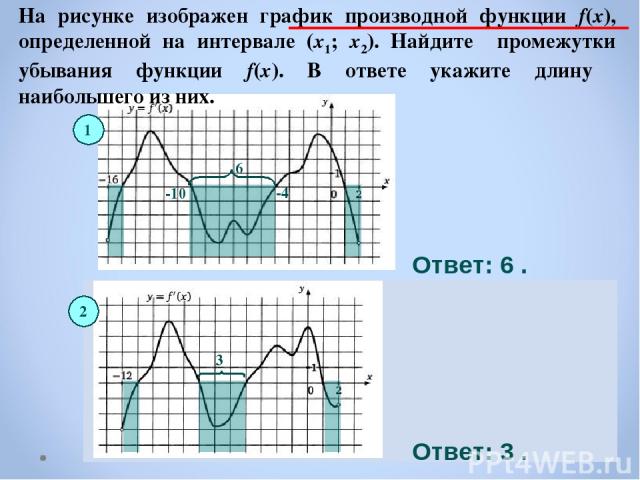
На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. 1 Ответ: 6 . Ответ: 3 . -10 -4 6 3 2

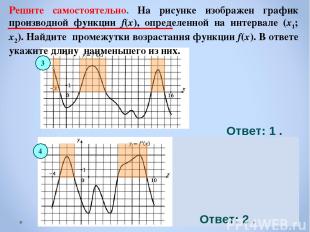
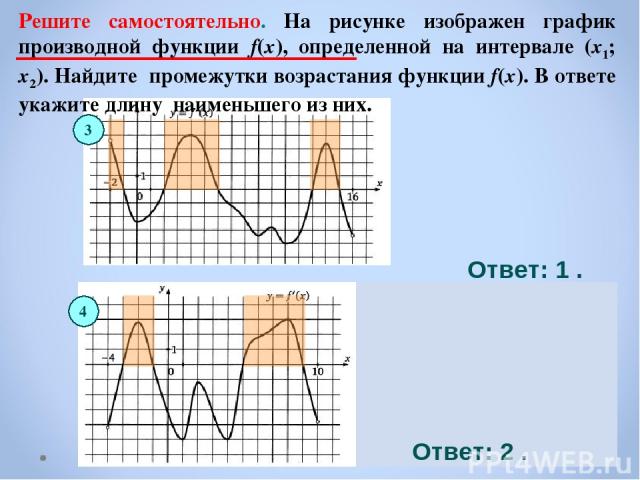
Решите самостоятельно. На рисунке изображен график производной функции f(x), определенной на интервале (x1; x2). Найдите промежутки возрастания функции f(x). В ответе укажите длину наименьшего из них. 3 Ответ: 1 . Ответ: 2 . 4

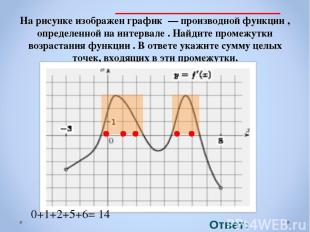
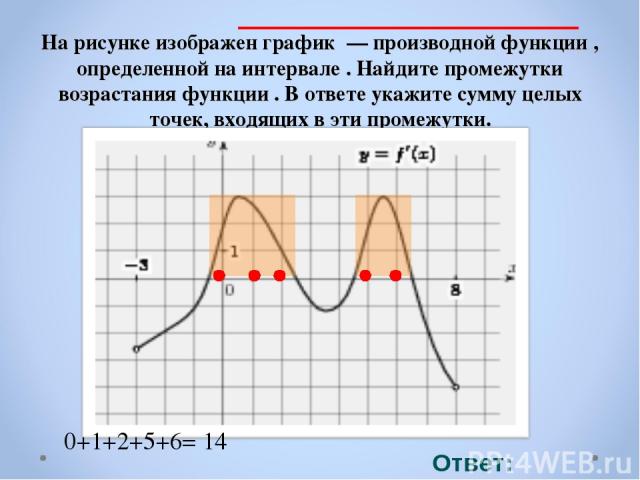
На рисунке изображен график  — производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки. Ответ: 14 . 0+1+2+5+6= 14

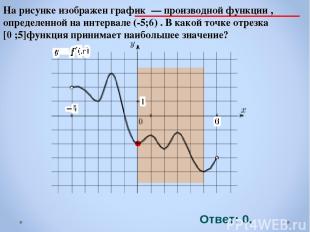
На рисунке изображен график  — производной функции , определенной на интервале (-5;6) . В какой точке отрезка [0 ;5]функция принимает наибольшее значение? Ответ: 0.

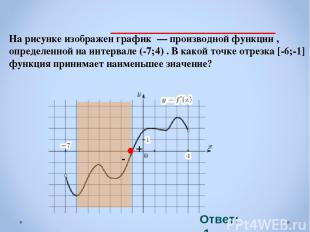
На рисунке изображен график  — производной функции , определенной на интервале (-7;4) . В какой точке отрезка [-6;-1] функция принимает наименьшее значение? Ответ: -1 . - +

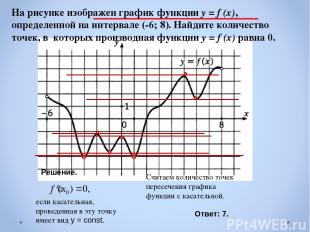
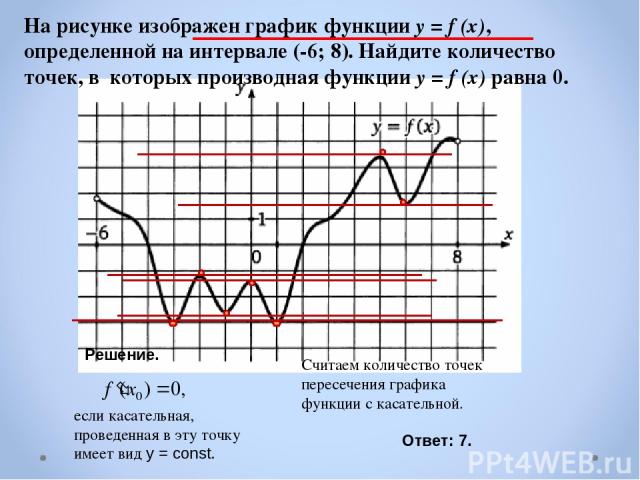
Решение. если касательная, проведенная в эту точку имеет вид у = const. Считаем количество точек пересечения графика функции с касательной. Ответ: 7. На рисунке изображен график функции y = f (x), определенной на интервале (-6; 8). Найдите количество точек, в которых производная функции y = f (x) равна 0.

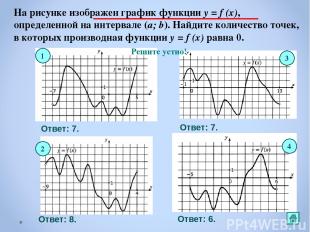
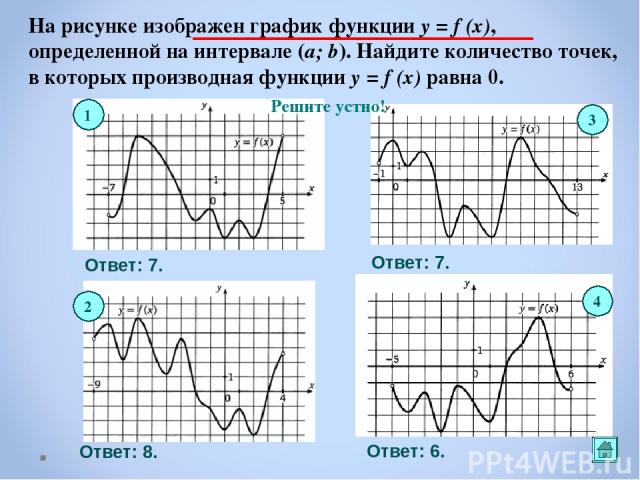
На рисунке изображен график функции y = f (x), определенной на интервале (a; b). Найдите количество точек, в которых производная функции y = f (x) равна 0. Ответ: 7. Ответ: 7. Ответ: 8. Ответ: 6. 1 3 4 2 Решите устно!

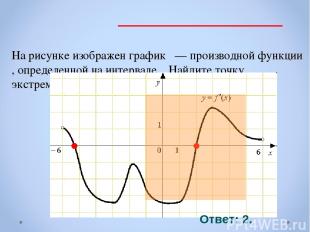
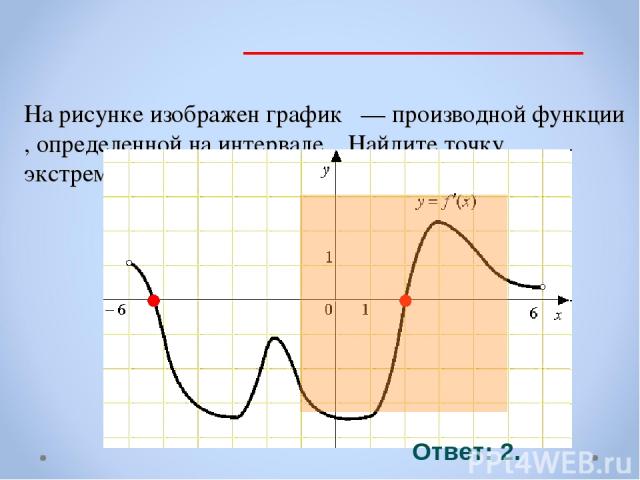
На рисунке изображен график  — производной функции , определенной на интервале . Найдите точку экстремума функции на интервале (-1;5) . Ответ: 2.

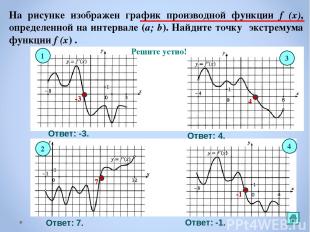
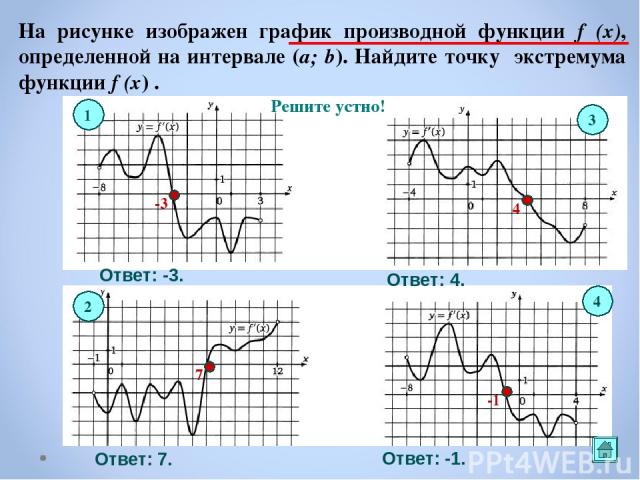
На рисунке изображен график производной функции f (x), определенной на интервале (a; b). Найдите точку экстремума функции f (x) . Решите устно! 1 3 4 2

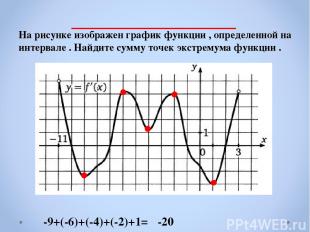
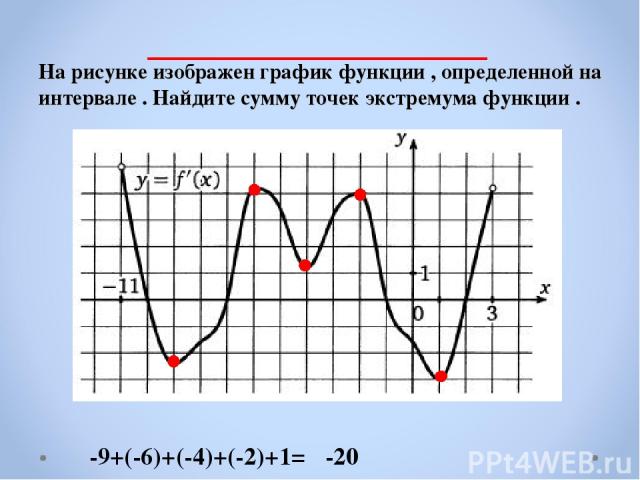
На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции . -9+(-6)+(-4)+(-2)+1= -20

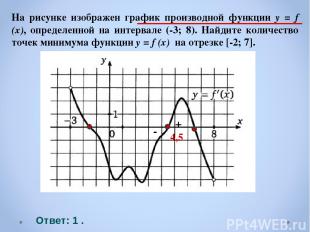
Ответ: 1 . 4,5 - + На рисунке изображен график производной функции y = f (x), определенной на интервале (-3; 8). Найдите количество точек минимума функции y = f (x) на отрезке [-2; 7].

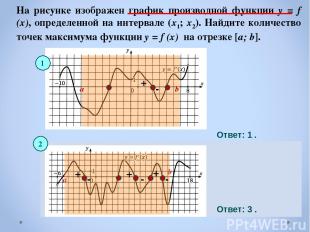
На рисунке изображен график производной функции y = f (x), определенной на интервале (x1; x2). Найдите количество точек максимума функции y = f (x) на отрезке [a; b]. Ответ: 1 . Ответ: 3 . a b a b - + 1 2

Алгоритм исследования непрерывной функции f(x) на монотонность и экстремумы. 1) Найти производную f `(x) . 2) Найти стационарные и критические точки. 3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. 4) Опираясь на Т.1, Т.2, Т.4, сделать выводы о монотонности функции и о её точках экстремума.

Промежутки возрастания, убывания f ′ (x) - ? f ′(x) > 0 в каждой точке интервала I f возрастает на I f ′(x) < 0 в каждой точке интервалаI f убывает на I + + - х1 х2 + + + - - - - х1 х1 х2 х2 х3 функция возрастает, функция убывает. f f ′ f f ′ f f ′

Найти критические точки функции. Определить, какие из них являются точками максимума, а какие – точками минимума. f (x) = 9+8x2-x4

Решение: f ′ =16х – 4х3; f ′ (х) определена во всех точках, f ′ = 0, 16х – 4х3 = 0, 4х (4 – х2) = 0, х=0 или (2-х)(2+х)=0 х=0, х =-2, х=2. В точке 0 производная меняет знак с «-» на «+» (f ′(х) < 0 при х (-∞;-2) U (-2; 0) и f ’(х) > 0 при х (0; 2) U (2; +∞)). Пользуясь признаками максимума и минимума, получаем, что точка 0 является точкой минимума fmin(x) = f(0) = 9. f ’ f min 0 -2 2 + + - -

№ 44.59.(а) Исследуйте функцию на монотонность и экстремумы