Презентация на тему: Длина дуги окружности

Длина дуги окружности

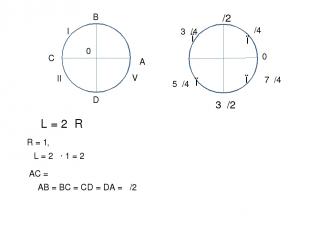
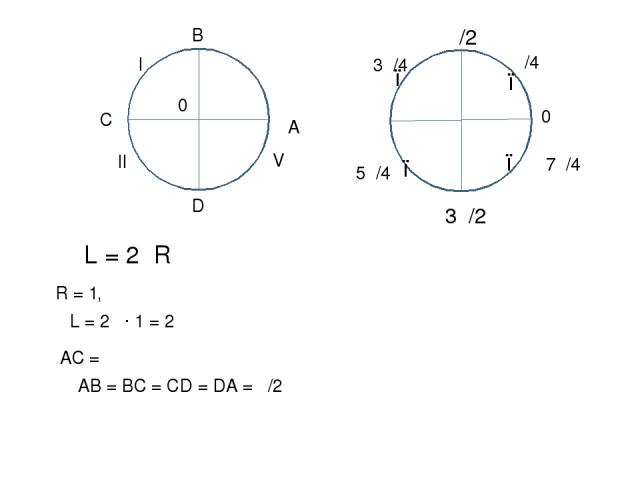
3π/4 В С D 0 Ι ΙІ ІІΙ ΙV L = 2πR R = 1, L = 2π ∙ 1 = 2π АС = π АВ = ВС = СD = DA = π/2 π 0 π/2 3π/2 А 5π/4 7π/4 π/4 ● ● ● ●

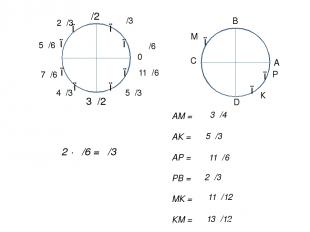
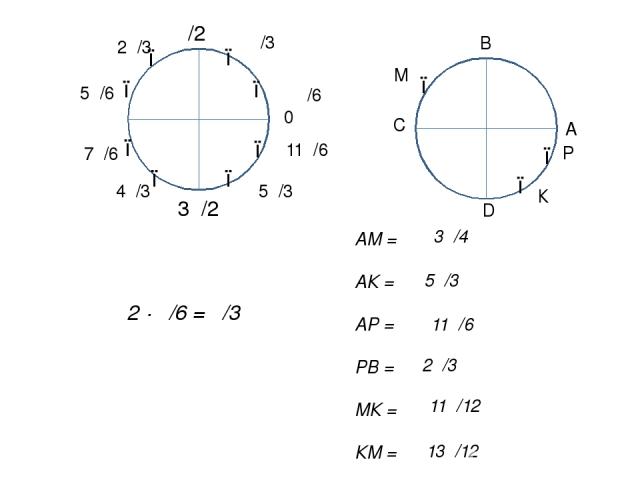
● ● ● ● ● ● ● ● 3π/2 π π/2 4π/3 π/3 2π/3 5π/6 7π/6 π/6 11π/6 5π/3 0 2 ∙ π/6 = π/3 ● ● ● М К Р С А В D АМ = АК = АР = РВ = МК = КМ = 3π/4 5π/3 11π/6 2π/3 11π/12 13π/12

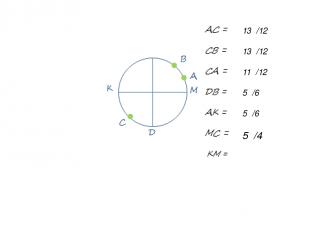
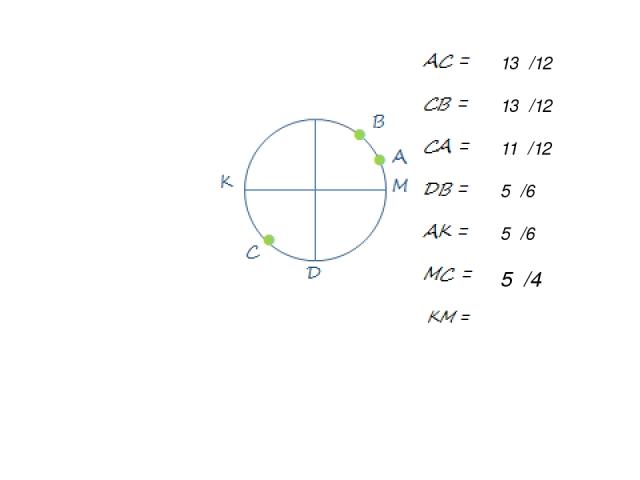
13π/12 13π/12 11π/12 5π/6 5π/6 5π/4 π

Числовая окружность Д/з № 28, на повторение № 21(стр. 279), №44(а) (стр. 281)

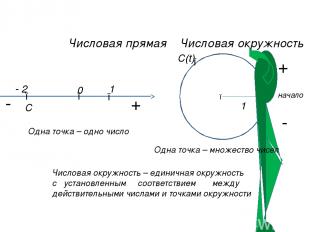
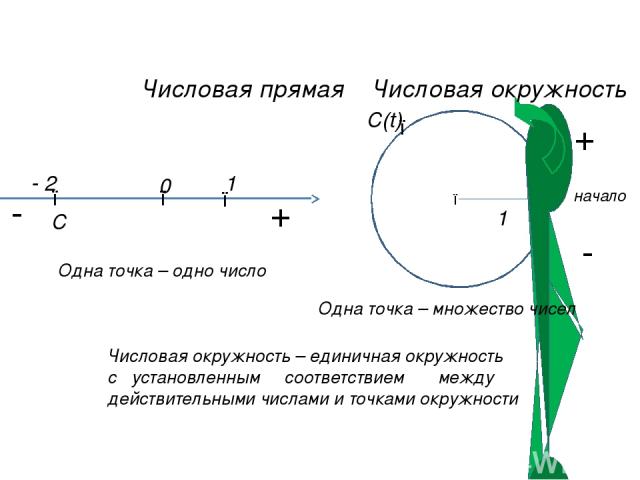
● 0 ● ● начало 1 + - Числовая прямая Числовая окружность Одна точка – одно число Одна точка – множество чисел Числовая окружность – единичная окружность с установленным соответствием между действительными числами и точками окружности ● ● - 2 1 С С(t) ● + -

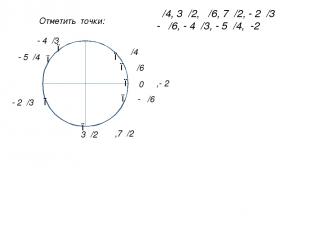
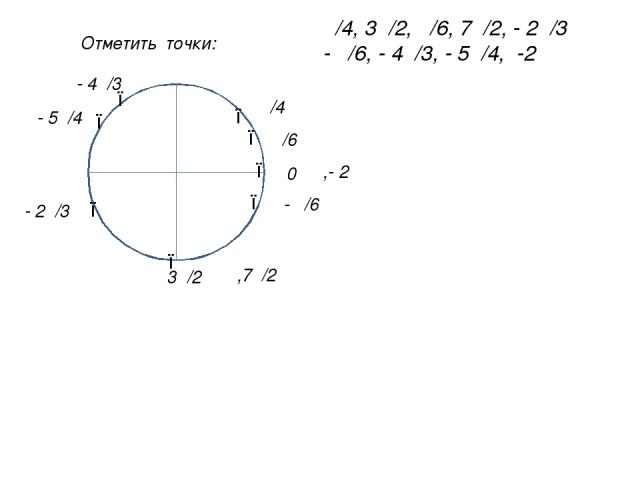
π/4, 3π/2, π/6, 7π/2, - 2π/3 - π/6, - 4π/3, - 5π/4, -2π ● ● ● ● ● ● ● 0 π/4 3π/2 π/6 ,7π/2 - π/6 - 4π/3 - 5π/4 ,- 2π - 2π/3 ● Отметить точки:

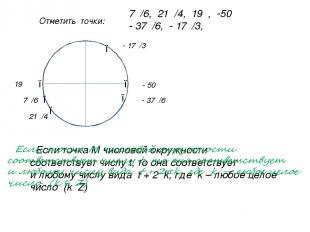
Отметить точки: 7π/6, 21π/4, 19π, -50π - 37π/6, - 17π/3, ● ● ● ● ● 7π/6 21π/4 ● 19π - 50π - 37π/6 - 17π/3

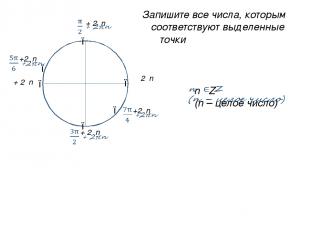
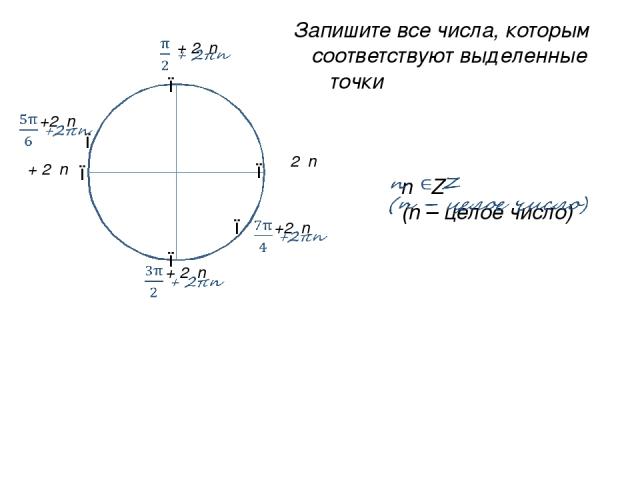
● ● ● ● ● Запишите все числа, которым соответствуют выделенные точки ● 2πn π + 2πn

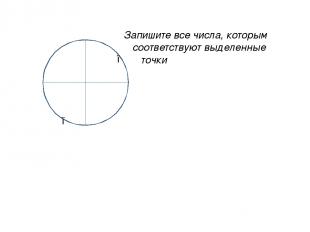
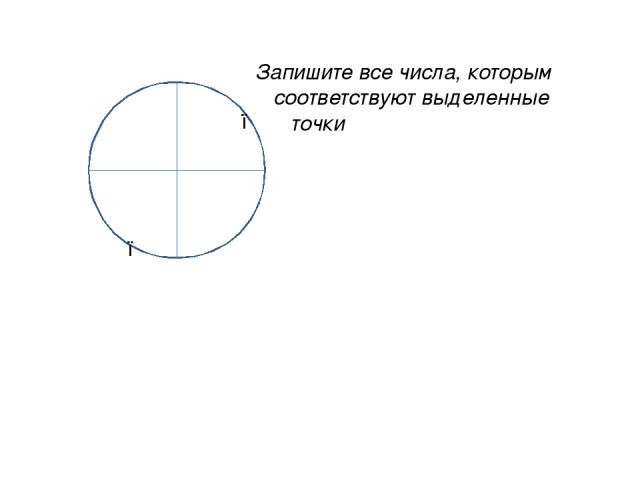
● ● Запишите все числа, которым соответствуют выделенные точки

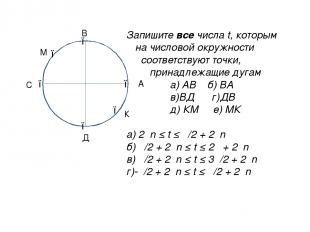
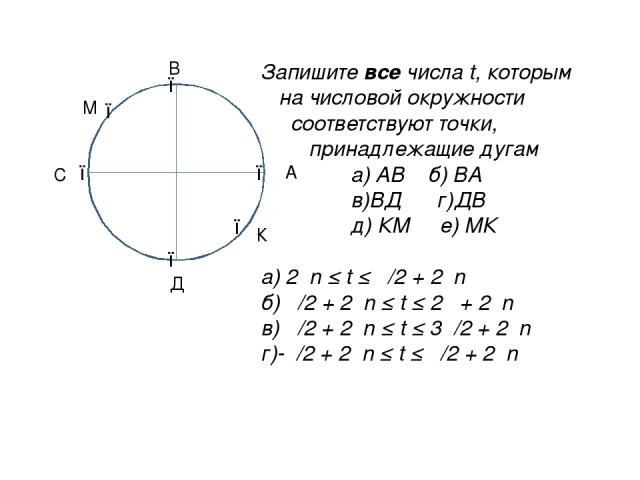
● ● ● ● ● Запишите все числа t, которым на числовой окружности соответствуют точки, принадлежащие дугам а) АВ б) ВА в)ВД г)ДВ д) КМ е) МК а) 2πn ≤ t ≤ π/2 + 2πn б) π/2 + 2πn ≤ t ≤ 2π + 2πn в) π/2 + 2πn ≤ t ≤ 3π/2 + 2πn г)-π/2 + 2πn ≤ t ≤ π/2 + 2πn ● А В С Д К М

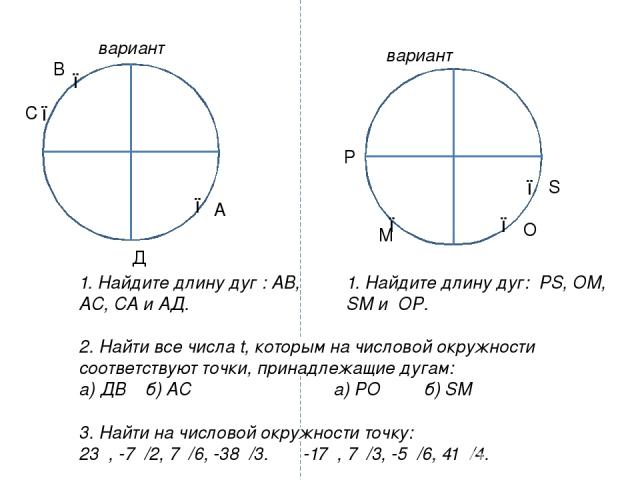
Ι вариант ΙΙ вариант ● ● ● ● ● ● С В А Д Р S O М 1. Найдите длину дуг : АВ, АС, СА и АД. 2. Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие дугам: а) ДВ б) АС а) РО б) SM 3. Найти на числовой окружности точку: 23π, -7π/2, 7π/6, -38π/3. -17π, 7π/3, -5π/6, 41π/4. 1. Найдите длину дуг: PS, OM, SM и ОР.

Числовая окружность в координатной Плоскости Д/з № 29. 34 (стр.20)

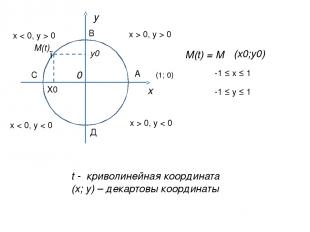
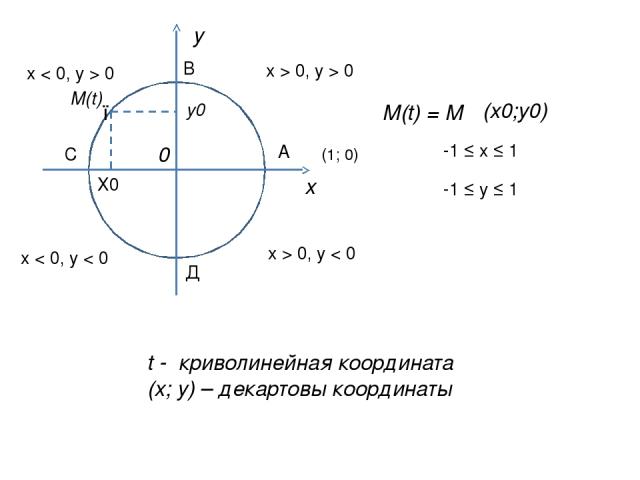
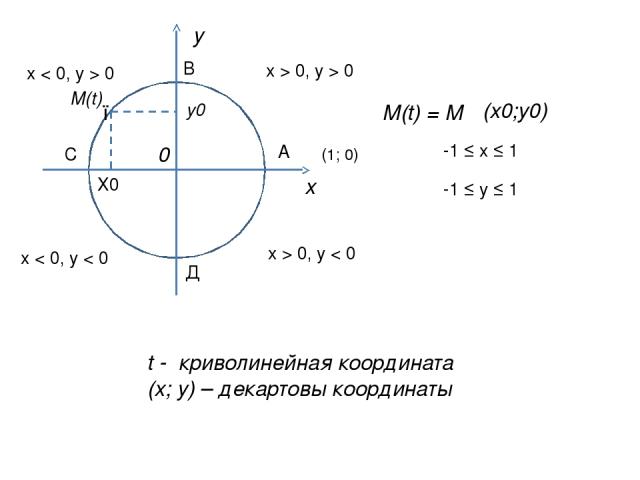
х у 0 ● М(t) Х0 у0 М(t) = М (х0;у0) В А С Д x > 0, y > 0 x < 0, y > 0 x > 0, y < 0 x < 0, y < 0 -1 ≤ x ≤ 1 -1 ≤ y ≤ 1 t - криволинейная координата (х; у) – декартовы координаты (1; 0)

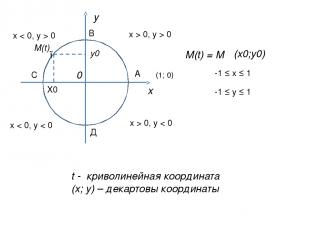
х у 0 ● М(t) Х0 у0 М(t) = М (х0;у0) В А С Д x > 0, y > 0 x < 0, y > 0 x > 0, y < 0 x < 0, y < 0 -1 ≤ x ≤ 1 -1 ≤ y ≤ 1 t - криволинейная координата (х; у) – декартовы координаты (1; 0)

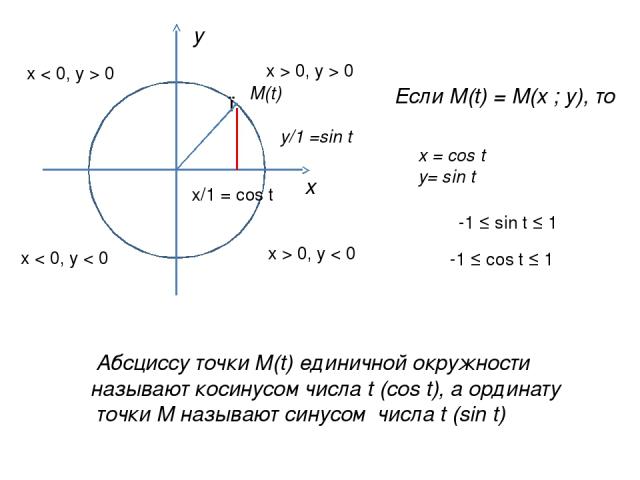
х у ● М(t) х/1 = сos t у/1 =sin t Если М(t) = М(х ; у), то x > 0, y > 0 x < 0, y > 0 x > 0, y < 0 x < 0, y < 0 -1 ≤ sin t ≤ 1 -1 ≤ cos t ≤ 1 Абсциссу точки М(t) единичной окружности называют косинусом числа t (сos t), а ординату точки М называют синусом числа t (sin t) х = cos t у= sin t