Презентация на тему: Теоремы Чевы и Менелая

Теоремы Чевы и Менелая Подготовила Ученица 8 класса «Б» Шебанкова Марина 5klass.net

Биография ученого Чева (Джованни) — итальянский математик. Умер в 1734 г. Главными предметами его занятий были геометрия и механика. Он написал много сочинений. Самым замечательным из них было первое "De lineis rectis se invicem secantibus statica constructio" (Милан, 1678); . В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек.

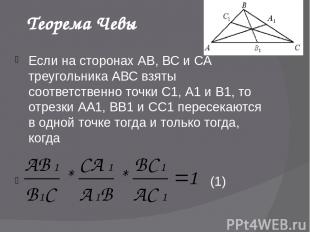
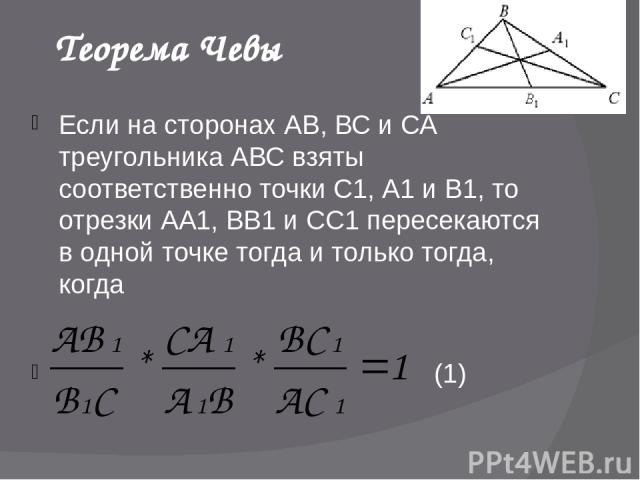
Теорема Чевы Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С1, А1 и В1, то отрезки АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда (1)

Пусть отрезки АА1, ВВ1 и СС1 пересекаются в точке О. Докажем,что По теореме о пропорциональных отрезках в треугольнике имеем: И Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем Разделив обе части на правую часть,приходим к равенству (1) О Доказательство.1.

УТВЕРЖДЕНИЕ ОБРАТНОЕ ТЕОРЕМЕ. Пусть для точек А1, В1, С1, взятых на соответствующих сторонах треугольника ABC, Выполняется равенство(1).Докажем, что отрезки АА1,BB1,СС1 пересекаются в одной точке. Обозначим точку пересечения отрезков АА1 и ВВ1 через О и проведем прямую СО. Она пересекает сторону АВ в точке С2. Т.к. отрезки АА1,ВВ1 и СС2 пересекаются в одной точке, то на основании доказанного в первом пункте (2) Итак, имеют место равенства (1) и (2) Сопоставляя их, приходим к равенству ,которое показывает, что точки С1 и С2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке О. Теорема доказана. О В С А С2 А1 В1

Биография ученого Менелай Александрийский (Menélaos), древнегреческий астроном и математик (1 в.). Автор работ по сферической тригонометрии: 6 книг о вычислении хорд и 3 книги «Сферики» (сохранились в арабском переводе). Тригонометрия у Менелая отделена от геометрии и астрономии. Арабские авторы упоминают также о книге Менелая по гидростатике.

Теорема Менелая Если на сторонах АВ, ВС и продолжении АС треугольника АВС соответственно взяты точки С1, А1 и В1, то эти точки лежат на одной прямой тогда и только тогда, когда (3) А1 С1 В1 В С А

Доказательство.1. Пусть точки А1, В1 и С1 лежат на одной прямой. Докажем, что Проведем прямые AD,BM и CN параллельно прямой В1А1. Согласно обобщению теоремы Фалеса имеем: и Перемножая левые и правые части этих равенств, получаем: , откуда D M N А1 С1 В1 В С А

УТВЕРЖДЕНИЕ ОБРАТНОЕ ТЕОРЕМЕ. Пусть точка В1 взята на продолжении стороны АС, а точки С1 и А1-на сторонах АВ и ВС, причем так, что выполнено равенство . Докажем, что точки А1, В1 и С1 лежат на одной прямой. А В С А1 С1 В1

Доказательство. Прямая В1С1 пересекает сторону ВС в некоторой точке А2.Т.к точки В1,С1 и А2 лежат на одной прямой, то по теореме Менелая (4) Сопоставляя (3) и (4),приходим к равенству ,которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении.Следовательно, точки А1 и А2 совпадают, и, значит, точки А1, В1 и С1 лежат на одной прямой. А В С А2 С1 В1

Задача.1 Дано: точка К делит сторону АВ равнобедренного треугольника АВС (АВ=АС) в отношении 2:1. Точка Р лежит на продолжении АС за точку С, и АВ=СР. Найти: в каком отношении делит прямая РК сторону ВС. А К В Х Р С

Решение. По условию и Используя теорему Менелая, мы находим А К В Х Р С

Задача 2. На медиане BD треугольника ABC отмечена точка М так, что ВМ:MD=m:n. Прямая АМ пересекает сторону ВС в точке К. найдите отношение ВК:КС. А В С M D К

Решение. По теореме Менелая: ВМ-медиана, значит А В С M D К

Задача 3. Через середину М стороны ВС треугольника АВС, в котором АВ≠АС, проведена прямая, параллельная биссектрисе угла А и пересекающая прямые АВ и АС соответственно в точках D и Е. Докажите, что BD=СЕ А В С M D N Е

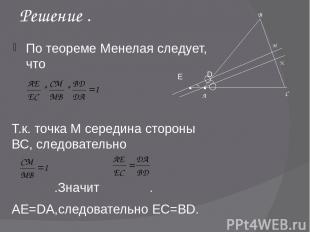
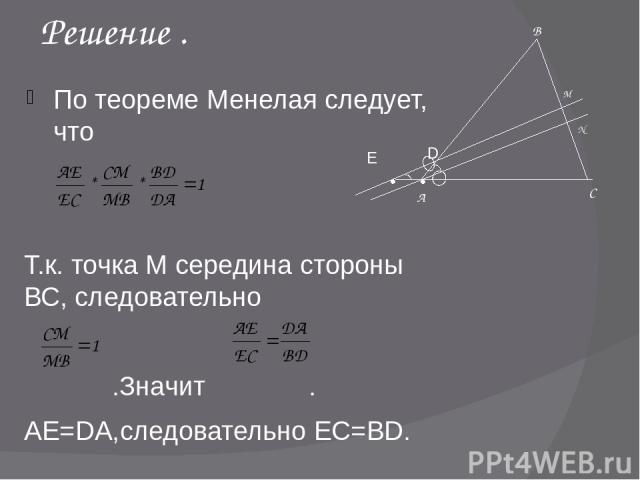
Решение . По теореме Менелая следует, что Т.к. точка М середина стороны ВС, следовательно .Значит . АЕ=DA,следовательно ЕС=BD. А В С M D N Е