Презентация на тему: Теорема Пифагора для треугольника

Урок геометрии в 8 классе на тему «Теорема Пифагора» Учитель математики МОУ СОШ № 4 им. Н.А. Некрасова с углубленным изучением английского языка г.Ярославля Сафронова Нина Вениаминовна ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА: учебник «Геометрия 7-9 классы», Л.С.Атанасян Корикова Т.М., Суслова И.В., Ястребов А.В. «Методика работы с теоремой», издательство ЯГПУ, 2010 г. Литцман С.Я. «Теорема Пифагора», Физматгиз, 1960 ЦЕЛЬ УРОКА: ОБРАЗОВАТЕЛЬНЫЕ ЦЕЛИ: вести теорему Пифагора, показать ее применение к решению задач (формировать умения применять на следующих уроках) РАЗВИВАЮЩИЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ: развитие самостоятельной и познавательной деятельности учащихся развитие активности и интереса к математике умение применять информационные технологии в доказательстве теоремы 5klass.net

Теорема Пифагора Легенды и факты о Пифагоре. Авторы презентации : Власенко Д., Белохвостова Т., Слизкова П., Матвеева П., Муравьева А. Пифагорейская школа Авторы презентации : Чупрунов А., Рыжковская Д., Растворова А., Быстрицкая У. Доказательство теоремы Пифагора (учебник «Геометрия 7-9 классы», Л.С.Атанасян) Авторы презентации : Гаврилова А, Емеличева В., Романова И. Применение теоремы Пифагора к решению задач Авторы презентации : Пестиков И., Ромашов С., Топоркова Е. Доказательство теоремы Пифагора Евклидом (Автор презентации : Буджиашвили Л. Другие доказательства теоремы Пифагора Авторы презентации : Устенко Д., Маслова М., Городецкая Е., Крайнова А.) г.Ярославль, СОШ № 4

Легенды и факты о Пифагоре Авторы: Власенко Даниил Белохвостова Татьяна Слизкова Полина Матвеева Полина Муравьева Алена

Пифагор

Юность Пифагора По преданию, Пифагор, сын Мнесарха, родился около 580 г. до н. э. на острове Самос. Первые познания он получил от своего отца, ювелира: в те времена эта профессия требовала многосторонней образованности. Для тогдашней греческой молодежи посещение чужих стран было главным способом расширить запас знаний, поэтому юность свою Пифагор провел в путешествиях. С его именем связано много легенд. Известно, что Пифагор посещал Египет и Вавилон.

Судьба Пифагора Отец мечтал, что сын будет продолжать его дело- ремесло золотых дел мастера. Но жизнь рассудила иначе. Будущий великий математик и философ в детстве обнаружил большие способности к наукам. У своего первого учителя Пифагор получает знания основ музыки и живописи. Учитель прививал юному Пифагору любовь к природе и ее тайнам.

Обучение Спустя несколько лет, по совету своего учителя Пифагор решает учиться в Египте, у жрецов. Попасть в Египет в то время было трудно, потому что страну фактически закрыли для греков. Но пока до Египта далеко. Он живет на острове недалеко от Египта у своего родственника. Пифагор учится астрологии, предсказанию затмений, тайнам чисел, медицине и другим обязательным для того времени наукам. Отуда путь Пифагора лежит в Милет - к знаменитому Фалесу, основателю первой в истории философской школы. От него принято вести историю греческой философии.

Наконец добравшись до Египта благодаря покровительству своих друзей Пифагор знакомится со жрецами. Ему удается проникнуть в «святая святых»- египетские храмы, куда чужестранцы не допускались. Чтобы приобщиться к тайнам египетских храмов, Пифагор, следуя традиции, принимает посвящение в сан жреца. Учеба Пифагора в Египте способствует тому, что он сделался одним из самых образованных людей своего времени.

Пифагор и Геометрия Многое сделал ученый в геометрии. Особенное внимание он уделял числам и их свойствам, стремясь познать смысл и природу вещей. Посредством чисел он пытался осмыслить вечные категории бытия, как справедливость, смерть, постоянство, мужчина, женщина и прочее. Число для Пифагора было и материей, и формой Вселенной. Пифагор и его последователи своими работами заложили основу очень важной области математики - теории чисел.

Последователи Философа В новое время, особенно благодаря бурному развитию естествознания, астрономии и математики, идеи Пифагора приобретают новых поклонников. Великие Коперник и Кеплер,, гениальный Леонардо да Винчи, английский астроном Эддингтон, подтвердивший в 1919 году теорию относительности, и многие другие ученые продолжают находить в научно-философском наследии Пифагора необходимое основание для установления закономерностей нашего мира.

Правила Пифагорейской школы Авторы: Чупрунов А., Рыжковская Д., Растворова А., Быстрицкая У.

Школа Пифагора История создания Жизнь учеников в школе Принципы обучения Правила школы

История создания Школа Пифагора создается как организация со строго ограниченным числом учеников из аристократии, и попасть в неё было непросто. Претендент должен был выдержать ряд тяжелейших испытаний. Другим законом организации было хранение тайны, несоблюдение которой строго каралось. В меню

Жизнь учеников в школе Пифагорейцы просыпались с рассветом, пели песни, аккомпанируя себе на лире, потом делали гимнастику, занимались теорией музыки, философией, математикой, астрономией и другими науками. Часто занятия проводились на открытом воздухе, в форме бесед. В меню

Принципы обучения Пифагоризм определил число как принцип, придав научному объекту универсальное значение (приём, использованный позже и другими философиями). В меню

Правила школы Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться. Не делай никогда того, чего не знаешь. Но научись всему, что следует знать... Не пренебрегай здоровьем своего тела… Приучайся жить просто и без роскоши. Не закрывай глаз, когда хочется спать, не разобравши всех своих поступков в прошлый день. В меню

Спасибо за внимание! “Понять Божественную Суть – вот назначение высшее души, что послана Творцом на Землю!” Пифагор

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

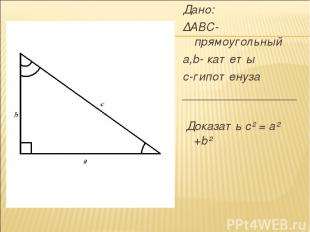
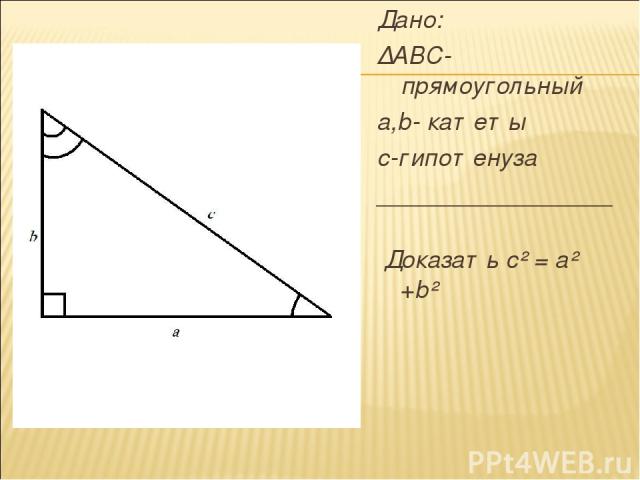
Дано: ∆ABC-прямоугольный a,b- катеты с-гипотенуза _________________ Доказать с² = а² +b²

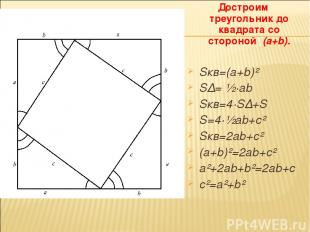
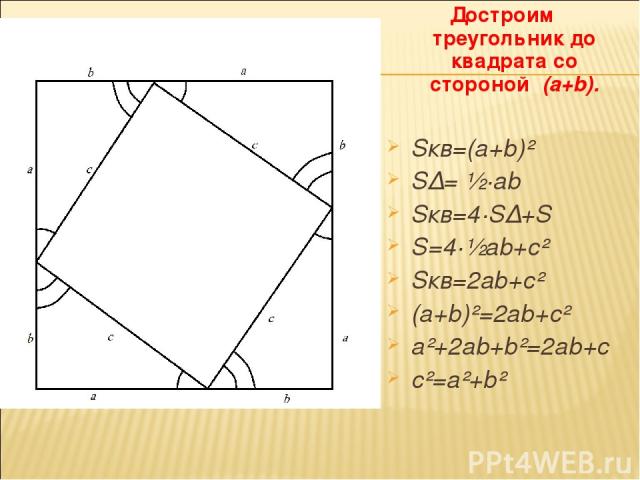
Достроим треугольник до квадрата со стороной (a+b). Sкв=(a+b)² S∆= ½·ab Sкв=4·S∆+S S=4·½ab+c² Sкв=2ab+c² (a+b)²=2ab+c² a²+2ab+b²=2ab+c c²=a²+b²

Спасибо за просмотр

Применение теоремы Пифагора к решению прямоугольных треугольников: Находим гипотенузу по известным катетам Находим катет по гипотенузе и второму катету

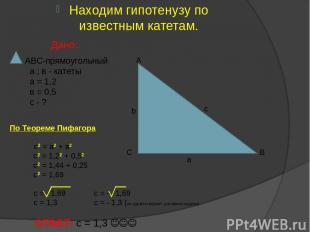
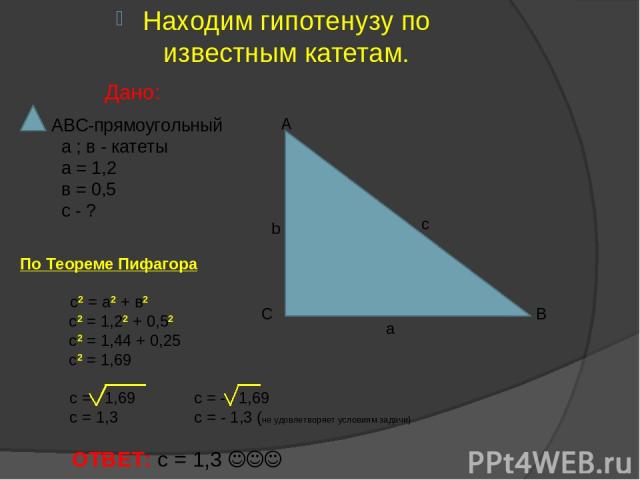
Находим гипотенузу по известным катетам. Дано: ABC-прямоугольный а ; в - катеты а = 1,2 в = 0,5 с - ? А В С a b c По Теореме Пифагора с2 = а2 + в2 с2 = 1,22 + 0,52 с2 = 1,44 + 0,25 с2 = 1,69 с = 1,69 с = - 1,69 с = 1,3 с = - 1,3 (не удовлетворяет условиям задачи) ОТВЕТ: с = 1,3

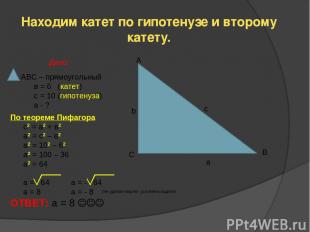
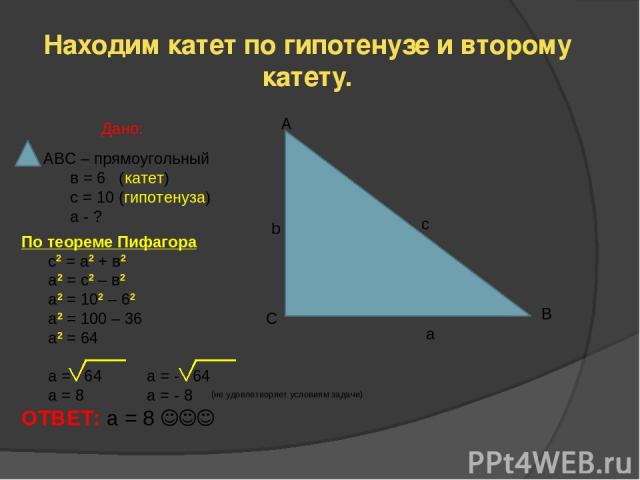
Находим катет по гипотенузе и второму катету. А b c С B a АВС – прямоугольный в = 6 (катет) с = 10 (гипотенуза) а - ? Дано: По теореме Пифагора с2 = а2 + в2 а2 = с2 – в2 а2 = 102 – 62 а2 = 100 – 36 а2 = 64 а = 64 a = - 64 a = 8 a = - 8 ОТВЕТ: а = 8 (не удовлетворяет условиям задачи)

Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками. Треугольники со сторонами 3,4,5 часто называют египетскими треугольниками.

Пестиков Игорь Ромашов Степан Топоркова Екатерина

доказательство

Теорема Пифагора

Доказательство Евклида Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".

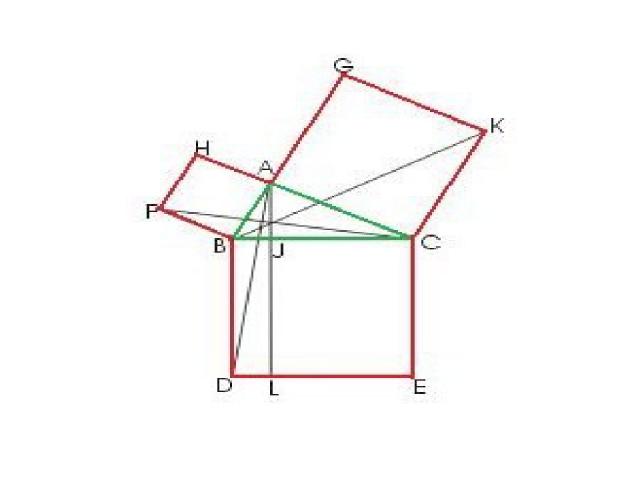
1) На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты

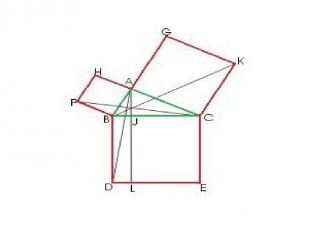
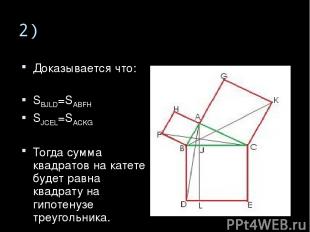
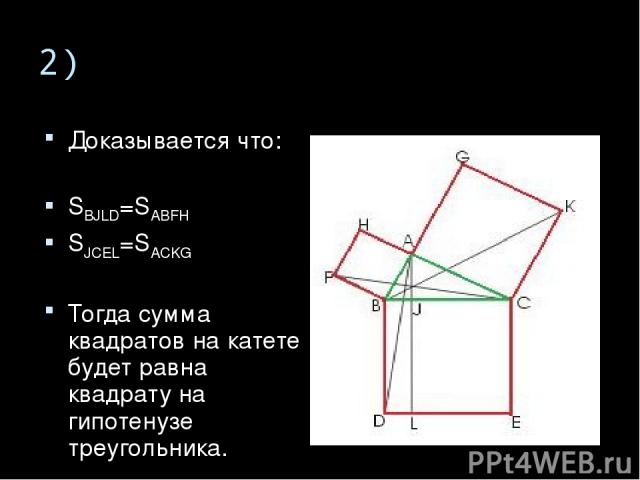
2) Доказывается что: SBJLD=SABFH SJCEL=SACKG Тогда сумма квадратов на катете будет равна квадрату на гипотенузе треугольника.

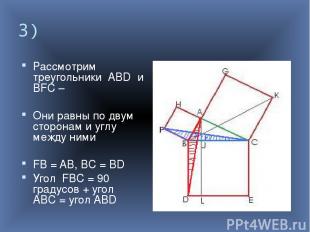
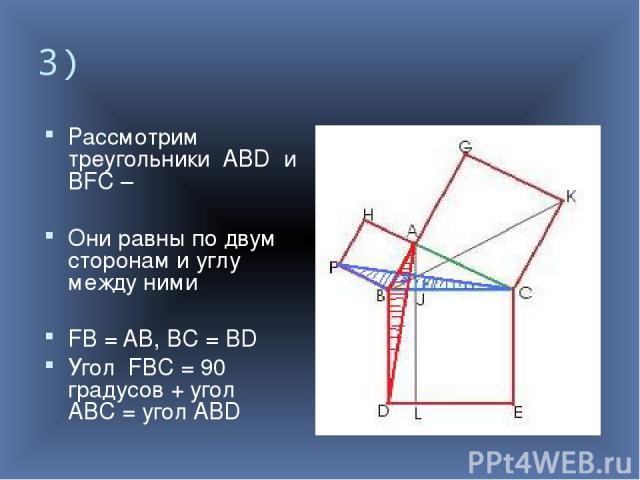
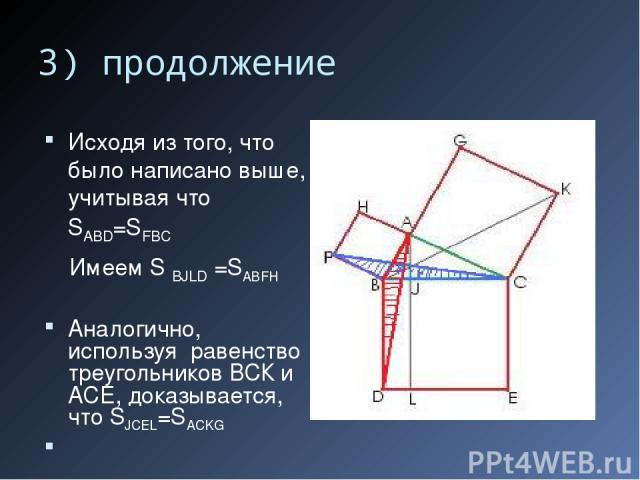
3) Рассмотрим треугольники ABD и BFC – Они равны по двум сторонам и углу между ними FB = AB, BC = BD Угол FBC = 90 градусов + угол ABC = угол ABD

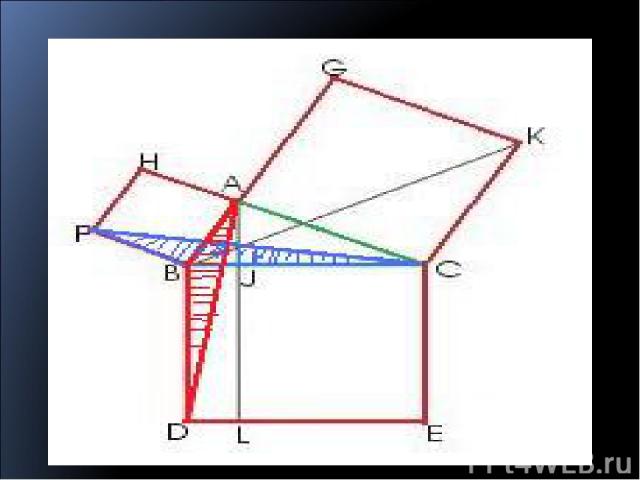
3) продолжение SABD = 1/2 S BJLD SFBC=1/2 S ABFH так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. (BF - общее основание, АВ - общая высота).

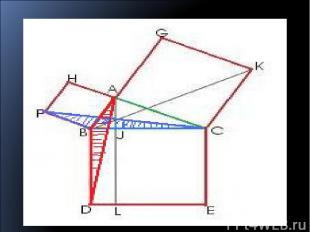
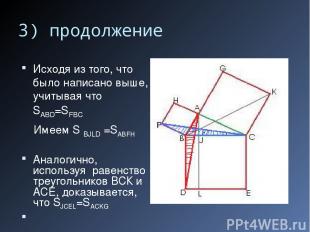
3) продолжение Исходя из того, что было написано выше, учитывая что SABD=SFBC Имеем S BJLD =SABFH Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что SJCEL=SACKG

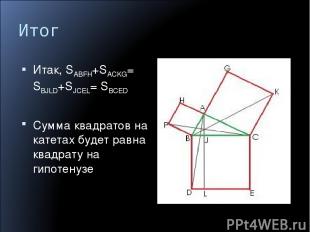
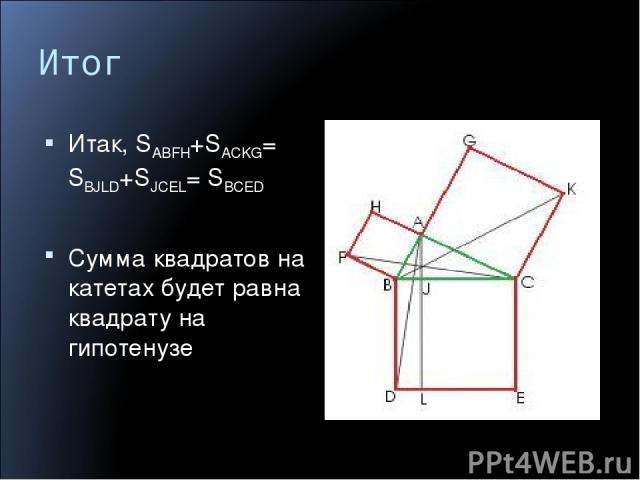
Итог Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED Сумма квадратов на катетах будет равна квадрату на гипотенузе

Автор презентации: Буджиашвили Леон

Теорема Пифагора

Дано: прямоугольный треугольник Катеты – a,b Гипотенуза - c Доказать: c2 =a2 +b2 a c b Прямоугольный треугольник достроим до квадрата со стороной (a + b)

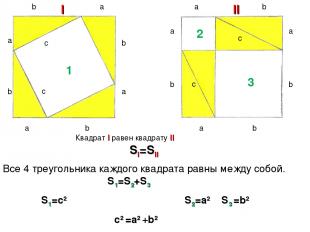
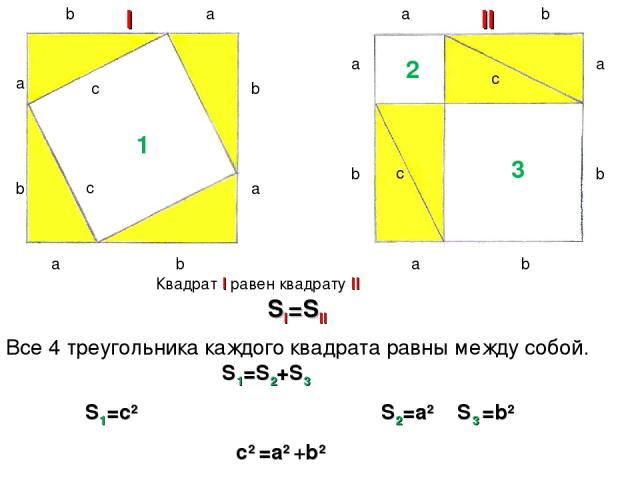
b a a a a a a a a b b b b b b b c c c c I II 1 2 3 Квадрат I равен квадрату II SI=SII Все 4 треугольника каждого квадрата равны между собой. S1=S2+S3 S1=c2 S2=a2 S3 =b2 c2 =a2 +b2

Над презентацией работали: Маслова Мария Устенко Дарья Городецкая Екатерина Крайнова Аполлинария

Над презентацией работали: Маслова Мария Устенко Дарья Городецкая Екатерина Крайнова Аполлинария