Презентация на тему: Теорема Пифагора для прямоугольного треугольника

Теорема Пифагора Презентацию сделала ученица 8 «а» класса Калашникова Анастасия 5klass.net

Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно -философской школы пифагор - ейцев. Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров.

Ещё Геродот называл его «величайшим эллинским мудрецом». Самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных. В честь Пифагора назван кратер на Луне.


Учение Пифагора следует разбить на две составляющие части: научный подход к познанию мира и религиозно-мистический образ жизни, проповедуемый Пифагором. Доподлинно неизвестны заслуги Пифагора в первой части, так как ему позднее приписывали всё, созданное последователями в рамках школы пифагореизма. Вторая часть превалирует в учении Пифагора, и именно она осталась в сознании большинства античных авторов.

Монета с изображением Пифагора В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»

Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора - исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен): «В день, когда Пифагор открыл свой чертёж знаменитый, Славную он за него жертву быками воздвиг.»

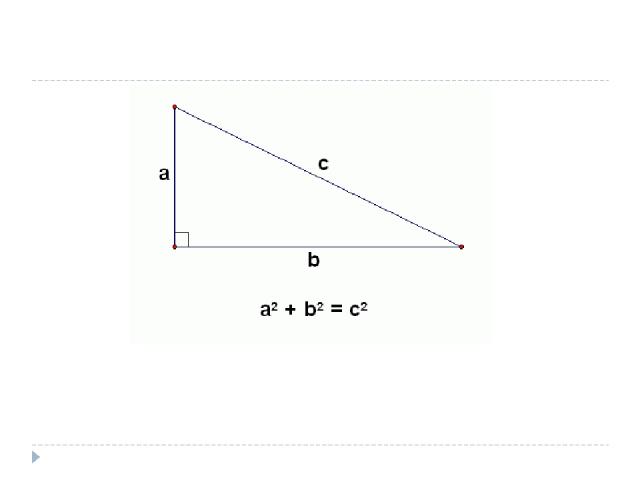
Изначально теорема была сформулирована следующим образом: или: Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
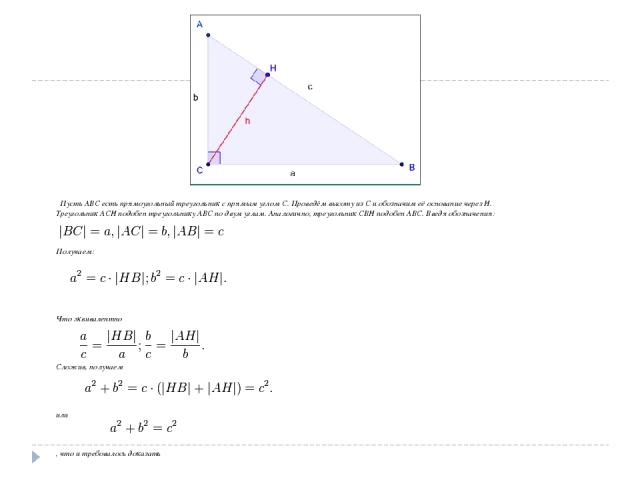
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения: Получаем: Что эквивалентно Сложив, получаем или , что и требовалось доказать

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о “пифагоровых штанах” — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна.

Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы свидетельствует о гигантском числе ее конкретных реализаций.

ссылки http://xreferat.ru/54/2139-1-teorema-pifagora.html http://ru.wikipedia.org/wiki/%CF%E8%F4%E0%E3%EE%F0 http://images.yandex.ru/ http://ru.wikipedia.org/wiki/