Презентация на тему: Тела Платона

Презентация на тему «Правильные многогранники или тела Платона» Выполнил Ученик 10 класса «Т1» Лицея №35 Носенко Игорь 5klass.net

Платон Платон (настоящее имя Аристокл) родился в Афинах в 428 или 427 году до нашей эры. Платону принадлежит разработка некоторых важных методологических проблем математического познания: аксиоматическое построение математики, исследование отношений между математическими методами и диалектикой, анализ основных форм математического знания. Так, процесс доказательства необходимо связывает набор доказанных положений в систему, в основе которой лежат некоторые недоказуемые положения. Тот факт, что начала математических наук "суть предположения", может вызвать сомнение в истинности всех последующих построений. Платон считал такое сомнение необоснованным. Согласно его объяснению, хотя сами математические науки, "пользуясь предположениями, оставляют их в неподвижности и не могут дать для них основания", предположения находят основания посредством диалектики. Платон высказал и ряд других положений, оказавшихся плодотворными для развития математики. Так, в диалоге "Пир" выдвигается понятие предела; идея выступает здесь как предел становления вещи.

Тела Платона Тела Платона-это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета суммы плоских углов при вершине, выпуклых правильных многогранников не больше пяти. Указанным ниже путем можно доказать, что существует именно пять правильных многогранников (это доказал Евклид). Они - правильный тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.

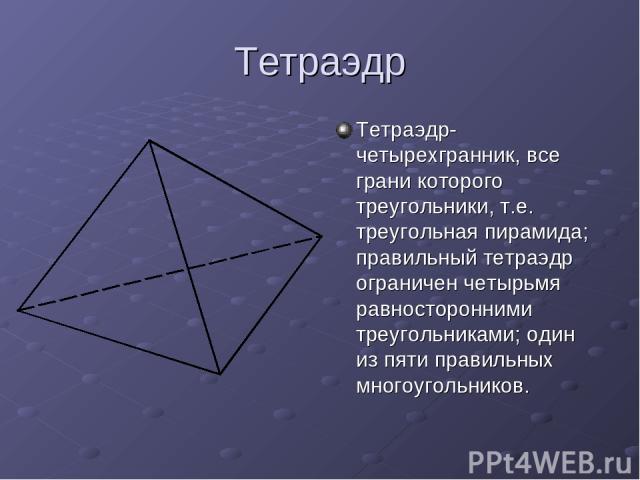
Тетраэдр Тетраэдр-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников.

Гексаэдр (куб) Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.

Октаэдр Октаэдр-восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников.

Додекаэдр Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников

Икосаэдр Икосаэдр-двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников

Дуальность Куб и октаэдр дуальны, т.е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны додекаэдр и икосаэдр.

Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, XII книга знаменитых начал Евклида. Эти многогранники часто называют также платоновыми телами в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном. Четыре из них олицетворяли четыре стихии: тетраэдр-огонь, куб-землю, икосаэдр-воду и октаэдр-воздух; пятый же многогранник, додекаэдр, символизировал все мироздание его по латыни стали называть quinta essentia («пятая сущность»). Придумать правильный тетраэдр, куб, октаэдр, по-видимому, было не трудно, тем более что эти формы имеют природные кристаллы, например: куб-монокристалл поваренной соли (NaCl), октаэдр-монокристалл алюмокалиевых квасцов ((KalSO4)2*12H2O). Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS).