Презентация на тему: Теорема Пифагора

Теорема Пифагора

История теоремы

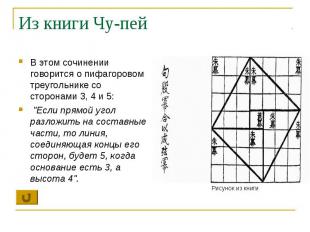
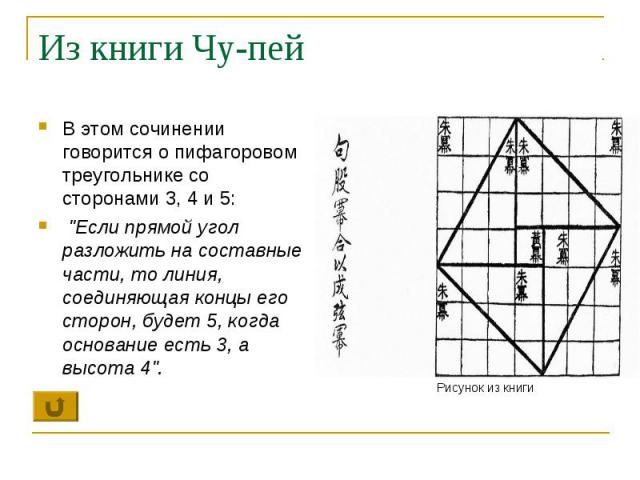
Из книги Чу-пей В этом сочинении говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".

Из папируса 6619  По мнению крупнейшего немецкого историка математики Кантора равенство 32 + 42 = 52 было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 

Теорема Пифагора в средние векаДоказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его  бегство "убогих", так как некоторые "ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее также "ветряной мельницей", составляли стихи вроде "Пифагоровы штаны на все стороны равны", рисовали карикатуры.

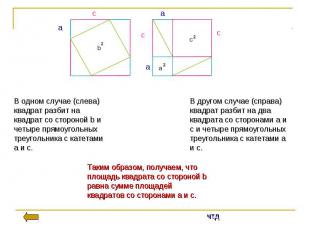
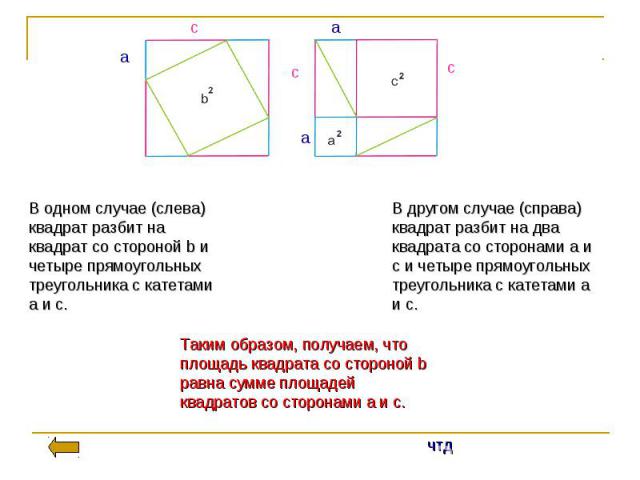
Формулировка теоремы Во времена Пифагора теорема звучала так: Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.или Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах

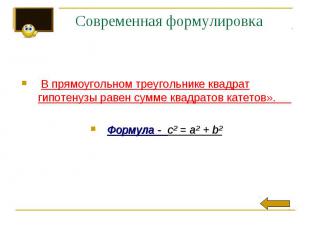
Современная формулировка В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».     Формула - c² = a² + b²

Доказательство