Презентация на тему: Сфера

Сфера Подготовила:учитель математикиМОУ сош №30 имени А.И.КолдуноваКутоманова Е.М.2010-2011 учебный год

1.Сфера и шар Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.Данная точка О- центр сферы.Данное расстояние R- радиус сферы.Отрезок, соединяющий любые две точки сферы и проходящий через центр, называется диаметром сферы.Тело, ограниченное сферой, называется шаром.Центр, радиус и диаметр сферы называются центром, радиусом и диаметром шара
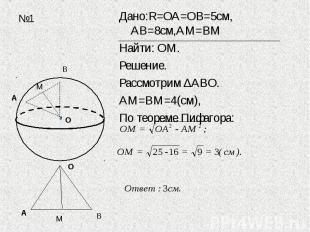
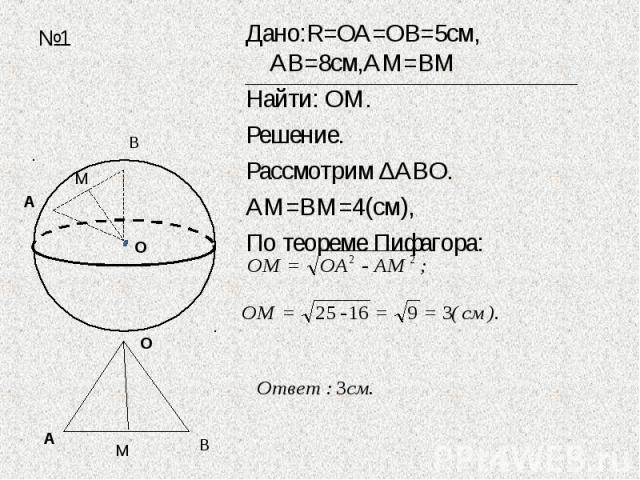
Дано:R=ОА=ОВ=5см, АВ=8см,АМ=ВМНайти: ОМ.Решение.Рассмотрим ∆АВО.АМ=ВМ=4(см),По теореме Пифагора:

2.Уравнение сферы Охуz- заданная прямоугольная система координат,С(х0;у0;z0)-центр сферы, М(х;у;z)- произвольная точка сферы.СМ²=(х-х₀)²+(у-у₀)²+(z-z₀)², (х-х₀)²+(у-у₀)²+(z-z₀)²=R²- уравнение сферы радиуса R с центром С(х0;у0;z0).

Дано:С(2;-1;5)-центр,R=3.Составьте уравнение сферы Решение.(х-х₀)²+(у-у₀)²+(z-z₀)²=R²- уравнение сферы радиуса R с центром С(х0;у0;z0).(х-2)²+(у+1)²+(z-5)²=3²,(х-2)²+(у+1)²+(z-5)²=9.Ответ:(х-2)²+(у+1)²+(z-5)²=9.

Дано:С(2;-1;5)-центр,А(1;5;-1)-точка сферы.Составьте уравнение сферы Решение.(х-х₀)²+(у-у₀)²+(z-z₀)²=R²- уравнение сферы радиуса R с центром С(х0;у0;z0).(х-2)²+(у+1)²+(z-5)²=R²,R²=(1-2)²+(5+1)²+(-1-5)²=1+36+36=73,(х-2)²+(у+1)²+(z-5)²=73.Ответ:(х-2)²+(у+1)²+(z-5)²=73.

№4 Найдите координаты центра сферы и её радиус. х²+у²+z²=16, (0;0;0)- центр сферы, R=4. (х-3)²+(у-6)²+(z+7)²=121, (3;6;-7)-центр сферы, R=11. (х+2)²+у²+(z-1)²=36, (-2;0;1)-центр сферы, R=6.

3.Взаимное расположение сферы и плоскости R-радиус сферы,d-расстояние от центра сферы до плоскости α.