Презентация на тему: Сфера

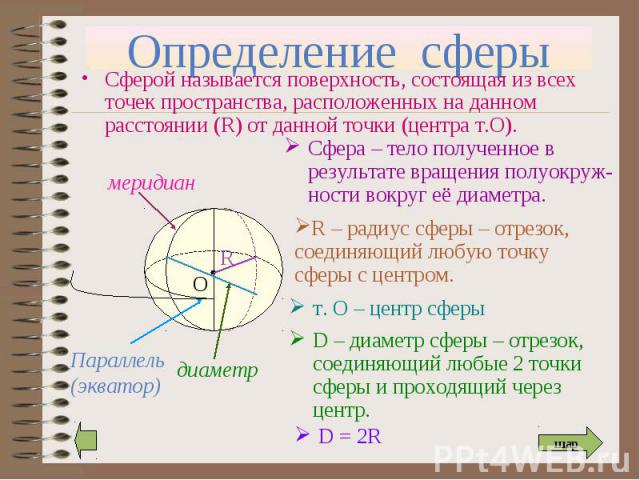
Определение сферы, шара. Определение сферы, шара. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы. Итог урока.

Часть плоскости, ограниченная окружностью, называется кругом. Часть плоскости, ограниченная окружностью, называется кругом.

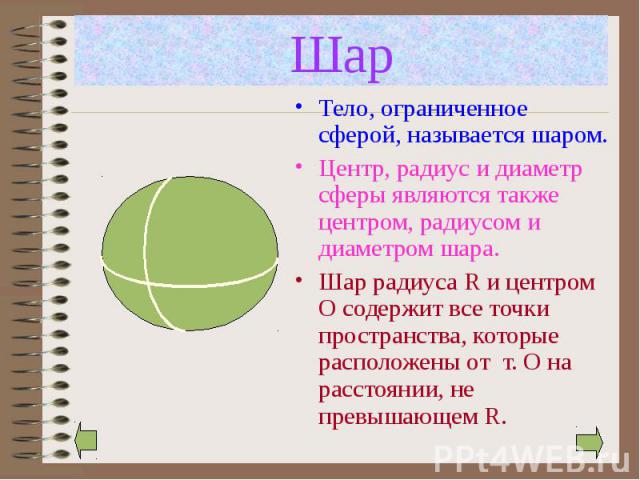
Тело, ограниченное сферой, называется шаром. Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара. Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.

Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» - мяч. Оба слова «шар» и «сфера» происходят от греческого слова «сфайра» - мяч. В древности сфера и шар были в большом почёте. Астрономические наблюдения над небесным сводом вызывали образ сферы. Пифагорейцы в своих полумистических рассуждениях утверждали, что сферические небесные тела располагаются друг от друга на расстоянии пропорциональном интервалам музыкальной гаммы. В этом усматривались элементы мировой гармонии. Отсюда пошло выражение «музыка сферы». Аристотель считал, что шарообразная форма, как наиболее совершенная, свойственна Солнцу, Земле, Луне и всем мировым телам. Так же он полагал, что Земля окружена рядом концентрических сфер. Сфера, шар всегда широко применялись в различных областях науки и техники.

следовательно уравнение следовательно уравнение окружности имеет вид: (x – x0)2 + (y – y0)2 = r2

Решение Решение так, как уравнение сферы с радиусом R и центром в точке С(х0;у0;z0) имеет вид (х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы (x-2)2 + (y+3)2 + z2=25 Ответ: (x-2)2 + (y+3)2 + z2=25

(x – x0)2 + (y – y0)2 + (z – z0)2 = R2 (x – x0)2 + (y – y0)2 + (z – z0)2 = R2

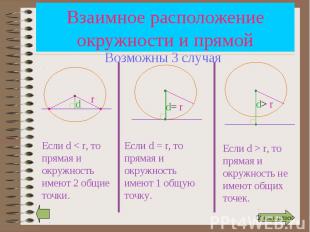
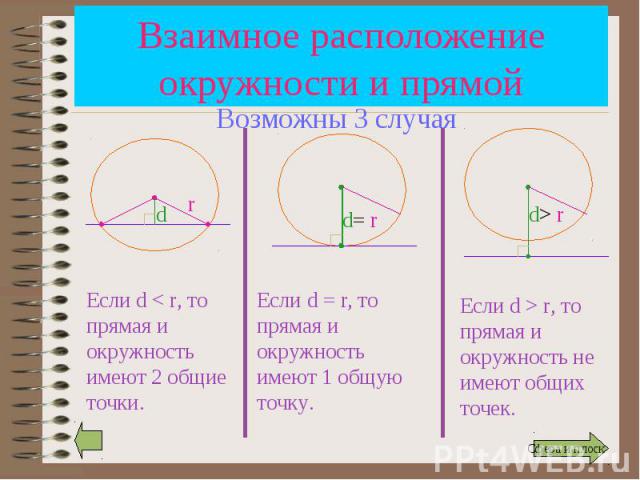
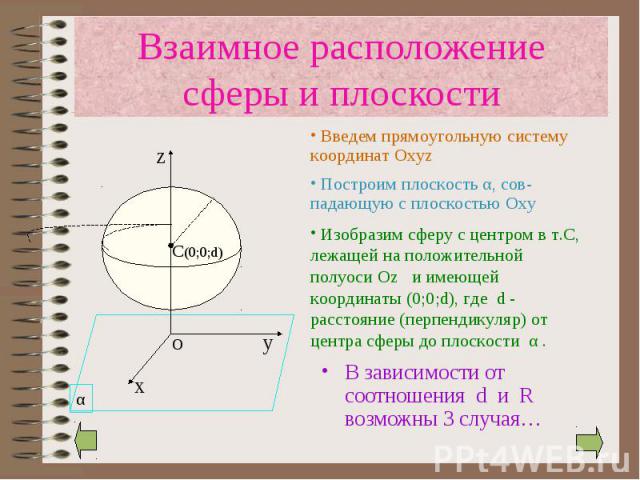
В зависимости от соотношения d и R возможны 3 случая… В зависимости от соотношения d и R возможны 3 случая…

Сечение шара плоскостью есть круг. Сечение шара плоскостью есть круг.

Дано: Дано: Шар с центром в т.О R=41 дм α - секущая плоскость d = 9 дм

Площадь сферы радиуса R: Sсф=4πR2 Площадь сферы радиуса R: Sсф=4πR2

Дано: Дано: сфера R = 6 см Найти: Sсф = ?

определением сферы, шара; определением сферы, шара; уравнением сферы; взаимным расположением сферы и плоскости; площадью поверхности сферы.