Презентация на тему: Сфера

Сфера

Примеры сферы:

Земля.

Шар для игры в гольф.

Определение сферыСферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от данной точки (центра т.О). R – радиус сферы – отрезок, соединяющий любую точку сферы с центром. D – диаметр сферы – отрезок,соединяющий любые 2 точки сферы и проходящий через центр.

Как изобразить сферу? 1. Отметить центр сферы (т.О) 2. Начертить окружность с центром в т.О 3. Изобразить видимую вертикальную дугу 4. Изобразить невидимуювертикальную дугу Изобразить видимую горизонтальную дугу 6. Изобразить невидимую горизонтальную дугу7. Провести радиус сферы R

Уравнение сферы Зададим прямоугольную систему координат Оxyz Построим сферу c центром в т. С и радиусом R МС = (x – x0)2 + (y – y0)2 + (z – z0)2 МС = R , или МС2 = R2 Следовательно, уравнение сферы имеет вид: (x – x0)2 + (y – y0)2 + (z – z0)2 = R2

Задача 1.Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы.

Решение: так как уравнение сферы с радиусом R и центром в точке С(х0;у0;z0) имеет вид (х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы (x-2)2 + (y+3)2 + z2=25 Ответ: (x-2)2 + (y+3)2 + z2=25

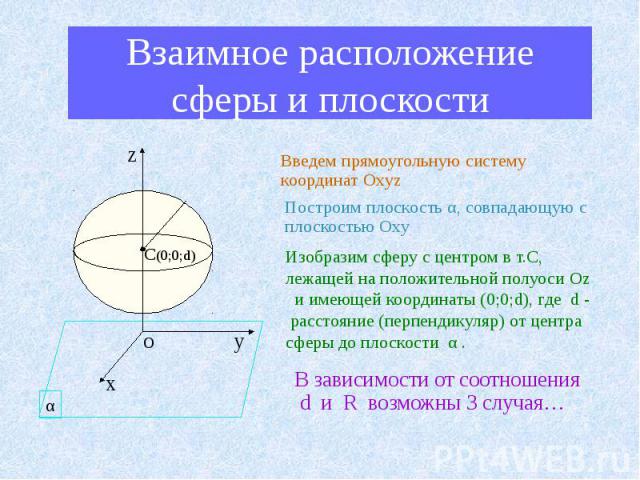
Взаимное расположение сферы и плоскости Введем прямоугольную систему координат Oxyz Построим плоскость α, совпадающую с плоскостью Оху Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d - расстояние (перпендикуляр) от центра сферы до плоскости α . В зависимости от соотношения d и R возможны 3 случая…

Взаимное расположение сферы и плоскости d < R, т.е. если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность радиусом r. r = R2 - d2 Сечение шара плоскостью есть круг.

Взаимное расположение сферы и плоскости Рассмотрим 2 случай: d = R, т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют одну общую точку

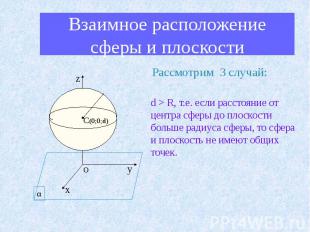
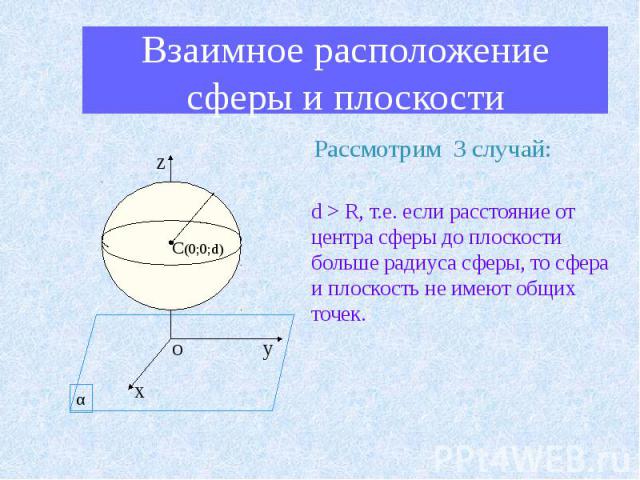
Взаимное расположение сферы и плоскости Рассмотрим 3 случай: d > R, т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Площадь сферы Сферу нельзя развернуть на плоскость. Опишем около сферы многогранник, так чтобы сфера касалась всех его граней. За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани Площадь сферы радиуса R: Sсф=4πR2 т.е.: площадь поверхности шара равна учетверенной площади большего круга Sшара=4 Sкруга

Задача 2.Найти площадь поверхности сферы, радиус которой равен 6 см.

Дано: сфера R = 6 смНайти: Sсф = ? Решение:Sсф = 4πR2Sсф = 4π 62 = 144π см2 Ответ: Sсф = 144π см2