Презентация на тему: Формула отрезков

Построение отрезка по формуле Проект по геометрии Выполнили: Филимонова Екатерина Руководитель: Шорина С.П. 900igr.net

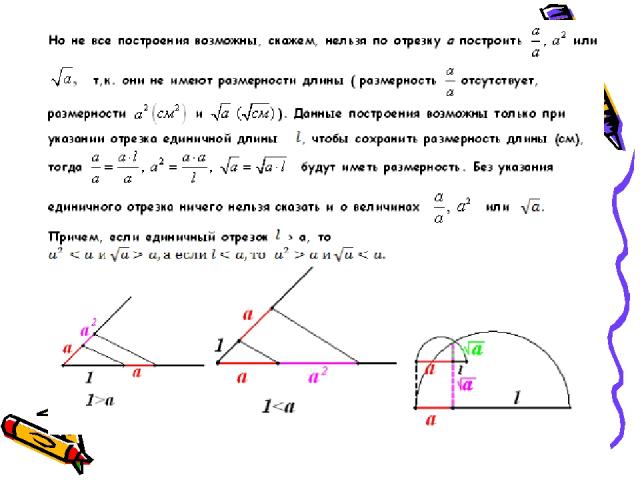
Теория. Общее определение. Особую часть задач на построение представляют собой задачи на построение по формуле, обычно они имеют следующий вид: исходя из данных отрезков (реже углов) построить отрезок (или угол), определяемый данной формулой. Иногда построение какого-либо объекта сводится к этой же задаче, если по данным в условии элементам удается недостающие элементы построения вычислить и по полученной формуле они строятся линейкой и циркулем.

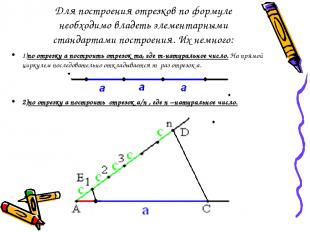
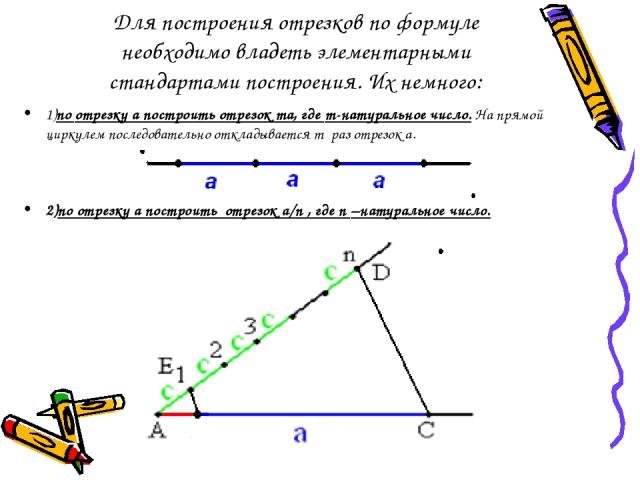
Для построения отрезков по формуле необходимо владеть элементарными стандартами построения. Их немного: 1)по отрезку а построить отрезок ma, где m-натуральное число. На прямой циркулем последовательно откладывается m раз отрезок а. 2)по отрезку а построить отрезок a/n , где n –натуральное число.

3)по отрезку а построить отрезок ma/n, где m и n –натуральные числа. Комбинация 1 и 2 построений. Сначала строим отрезок z, равный отрезку am, а потом отрезок z/n, равный отрезку ma/n. 4)по отрезкам a и b построить отрезки a+b и a-b (если a>b). Отложенный на прямой отрезок а увеличивается или уменьшается на отрезок b. 5) по отрезкам a, b и с построить отрезок х=ab/с (построение пропорциональных отрезков с использованием теоремы Фалеса: a/c=x/b )

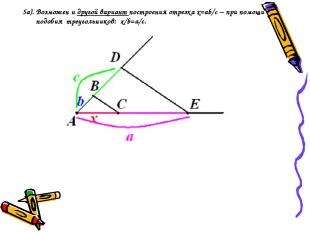
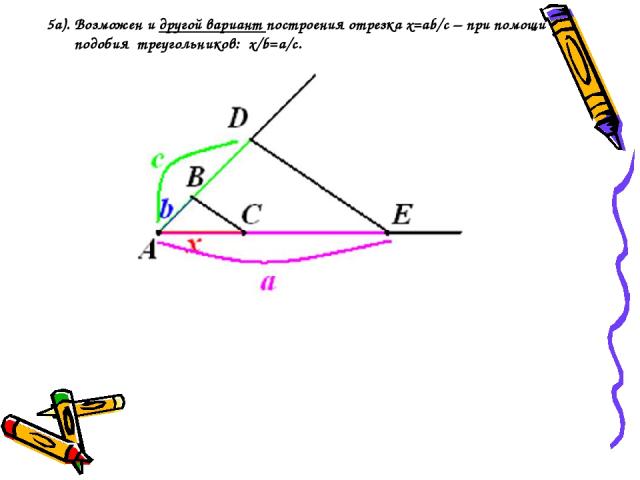
5a). Возможен и другой вариант построения отрезка х=ab/с – при помощи подобия треугольников: x/b=a/c.

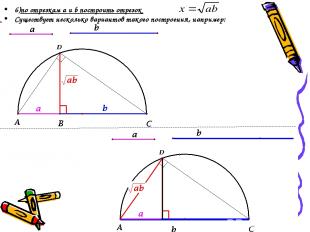
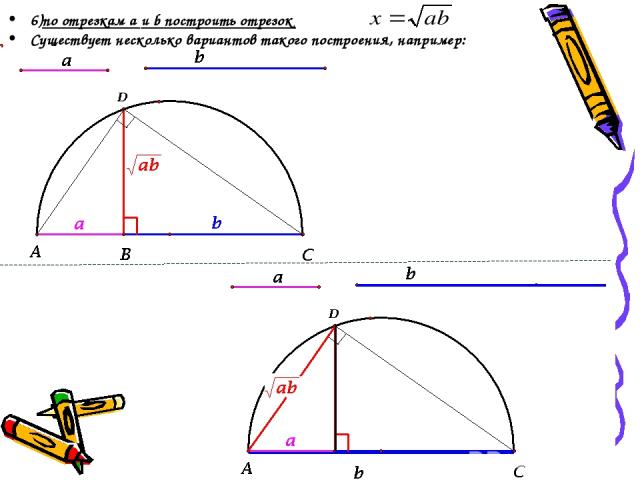
6)по отрезкам a и b построить отрезок Существует несколько вариантов такого построения, например:

Задача 1. Условие:По данным отрезкам a и b построить отрезок, заданный формулой Решение: Преобразовываем выражение: Вводим переменную: Получаем: Вводим еще одну переменную: Таким образом получаем: Данный отрезок мы можем построить без труда.

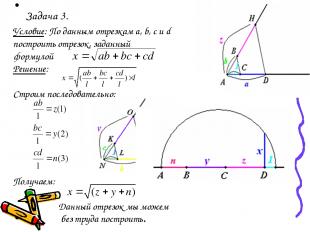
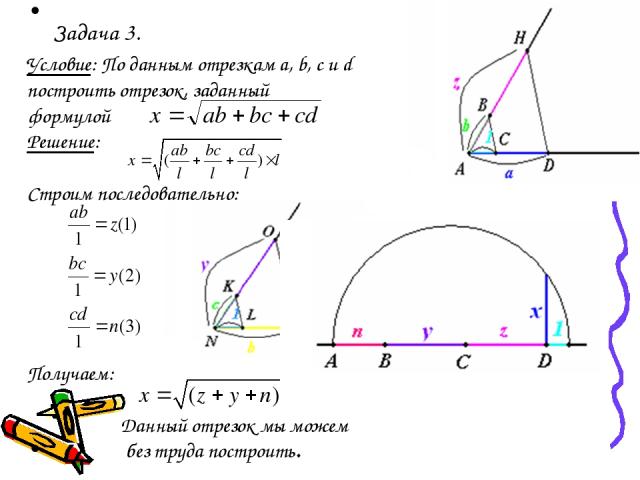
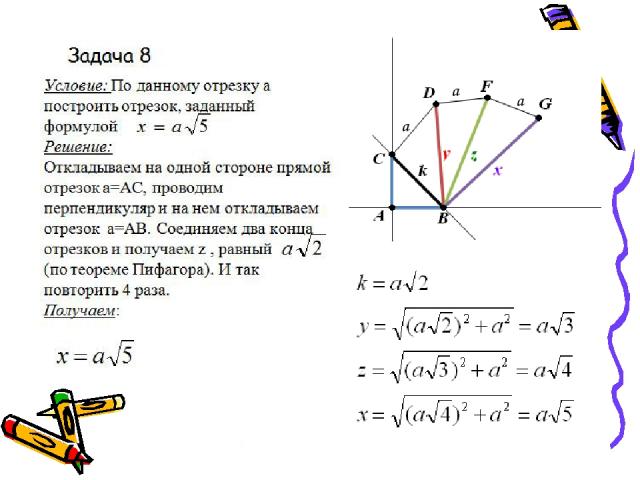
Задача 3. Условие: По данным отрезкам a, b, с и d построить отрезок, заданный формулой Решение: Строим последовательно: Получаем: Данный отрезок мы можем без труда построить.

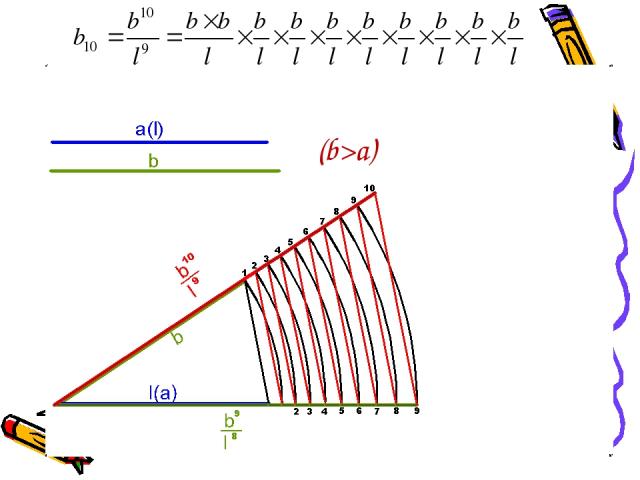
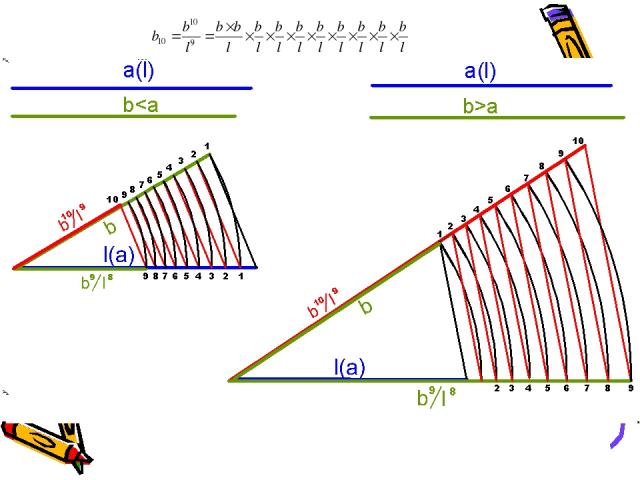
Задача 5.

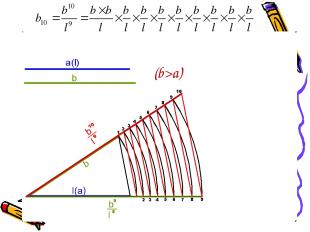
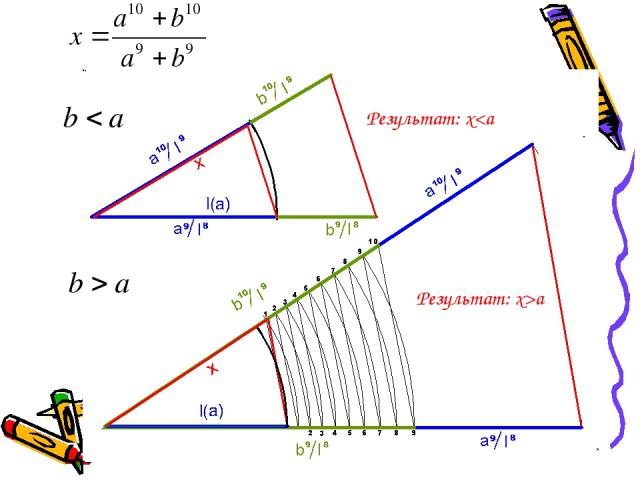
(b>a)

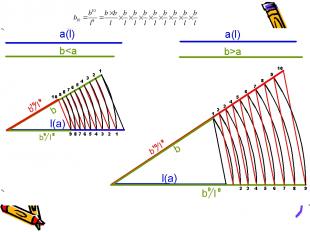
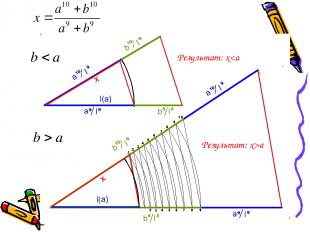
Результат: xa

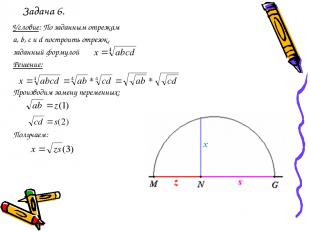
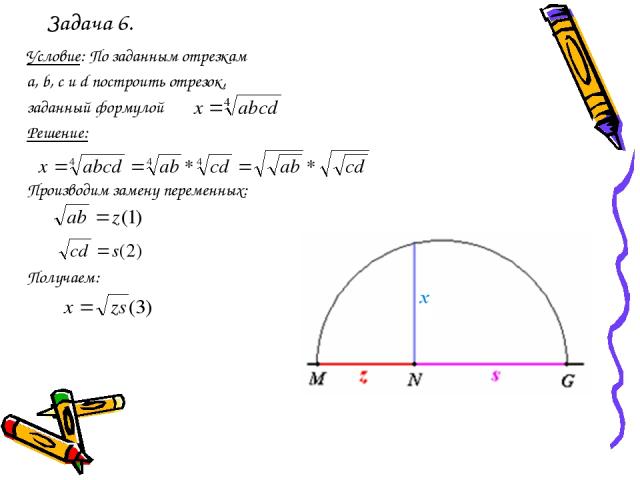
Задача 6. Условие: По заданным отрезкам a, b, с и d построить отрезок, заданный формулой Решение: Производим замену переменных: Получаем:

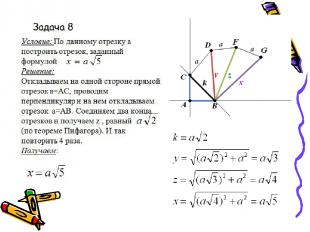
a a a a a a

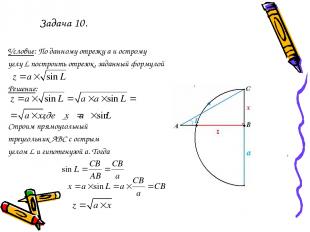
Задача 10. Условие: По данному отрезку а и острому углу L построить отрезок, заданный формулой Решение: Строим прямоугольный треугольник АВС с острым углом L и гипотенузой а. Тогда a