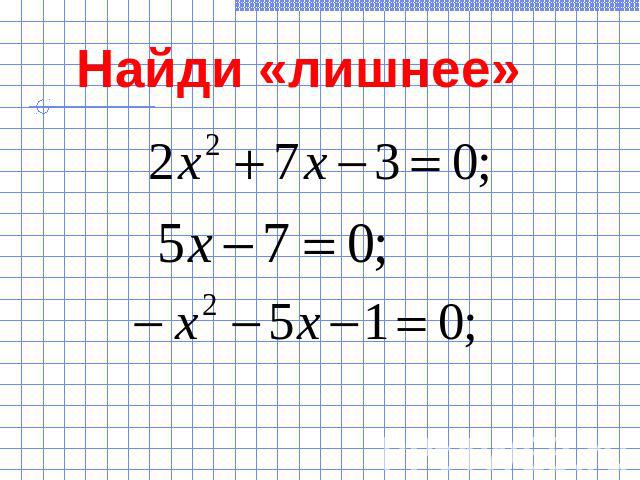Презентация на тему: Формула корней квадратного уравнения (8 класс)

Формула корней квадратного уравненияЛевшина Мария Александровнаучитель математики

Найди «лишнее»

Найди «лишнее»

Найди «лишнее»

Найди «лишнее»

Найди «лишнее»

Составьте квадратные уравнения, если известны их коэффициенты:а=3, b=8, c=2;2. а=1, b=0, c= -1;3. а=5, b=0,5, c= -3;

Простые уравнения люди научились решать более трех тысяч лет назад в Древнем Египте, Вавилоне и только 40 лет назад научились решать квадратные уравнения. Одним из тех, кто внес большой вклад в развития математики, был французский математик Виет (Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т. е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.

Дискриминант квадратного уравненияОпр. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac.Его обозначают буквой D, т.е. D= b2 – 4ac.Возможны три случая:D 0D 0

В этом случае уравнение ах2 + bх + с = 0 имеет два действительных корня:

В этом случае уравнение ах2 + bх + с = 0 имеет один действительный корень:

Уравнение ах2 + bх + с = 0 не имеет действительных корней.

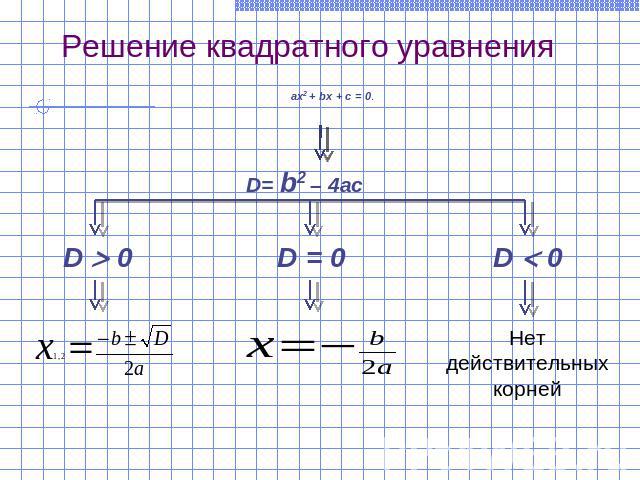
Решение квадратного уравнения

ЗадачиРешить уравнение 2x2- 5x + 2 = 0.Решить уравнение 2x2- 3x + 5 = 0.Решить уравнение x2- 2x + 1 = 0.

Решить уравнение 2x2- 5x + 2 = 0Здесь a = 2, b = -5, c = 2. Имеем D = b2- 4ac = (-5)2- 422 = 9. Так как D > 0, то уравнение имеет два корня.Найдем их по формуле

Решить уравнение 2x2- 3x + 5 = 0Здесь a = 2, b = -3, c = 5.Найдем дискриминант D = b2- 4ac== (-3)2- 4·2·5 = -31, т.к. D < 0, то уравнение не имеет действительных корней.

Решить уравнение x2- 2x + 1 = 0Здесь a = 1, b = -2, c = 1.Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0

№1. Решите уравнения:а) х2+7х-44=0;б) 9у2+6у+1=0;в) –2t2+8t+2=0;г) а+3а2= -11.д) х2-10х-39=0;е) 4у2-4у+1=0;ж) –3t2-12t+6=0;3) 4а2+5= а.№2. а)При какихзначениях х равны значения многочленов:(1-3х)(х+1) и (х-1)(х+1)?Б)При какихзначениях х равны значения многочленов:(2-х)(2х+1) и (х-2)(х+2)?

Ответы№1.А)х=-11, х=4Б)y=-1/3В)t=2±√5Г)нет решенияД)х=-3, х=13Е)у=1/2Ж)t=-2±√6З)нет решения№2А)х=1/2, х=-1Б)х=2, х=-1

Молодец !