Презентация на тему: «Формула корней квадратного уравнения»

ДА ДА

ДА ДА

ДА ДА

Определение квадратного уравнения Определение квадратного уравнения Дискриминант квадратного уравнения Формула корней квадратного уравнения Задачи Полезный материал Тест Самостоятельная работа

Опр. 1. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где х –переменная, а, b и с - некоторые числа, причем а 0. Опр. 1. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где х –переменная, а, b и с - некоторые числа, причем а 0. Числа а, b и с - коэффициенты квадратного уравнения. Число а называют первым коэффициентом, b – вторым коэффициентом и с – свободным членом.

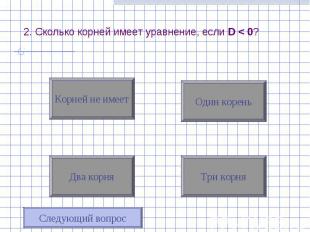
Опр. 2. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac. Его обозначают буквой D, т.е. D= b2 – 4ac. Опр. 2. Дискриминантом квадратного уравнения ах2 + bх + с = 0 называется выражение b2 – 4ac. Его обозначают буквой D, т.е. D= b2 – 4ac. Возможны три случая: D 0 D 0 D 0

В этом случае уравнение ах2 + bх + с = 0 имеет два действительных корня: В этом случае уравнение ах2 + bх + с = 0 имеет два действительных корня:

В этом случае уравнение ах2 + bх + с = 0 В этом случае уравнение ах2 + bх + с = 0 имеет один действительный корень:

Уравнение ах2 + bх + с = 0 не имеет действительных корней. Уравнение ах2 + bх + с = 0 не имеет действительных корней.

Обобщив рассмотренные случаи получаем Обобщив рассмотренные случаи получаем формулу корней квадратного уравнения ах2 + bх + с = 0.

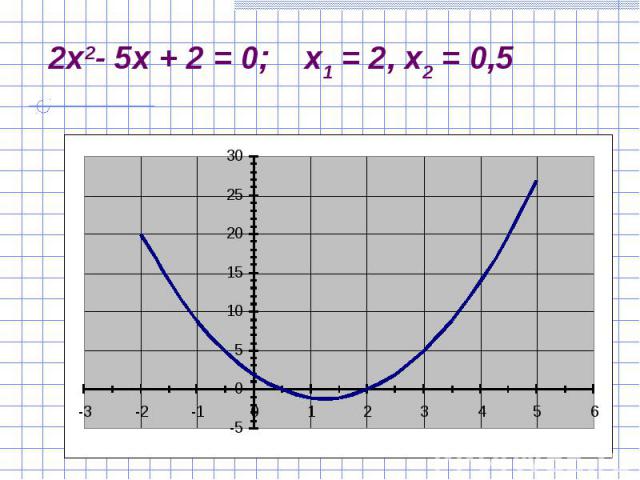
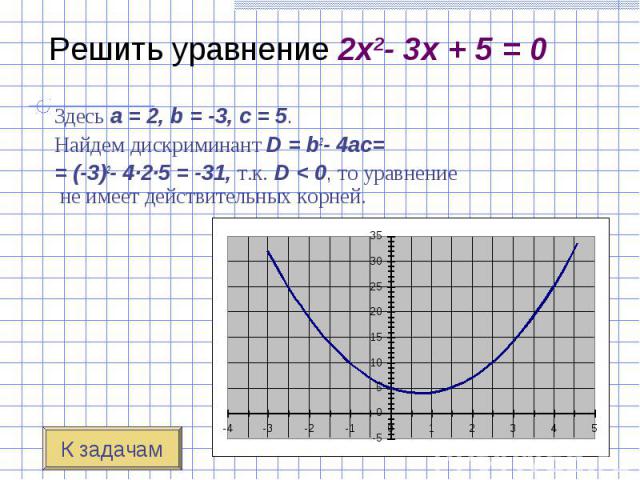
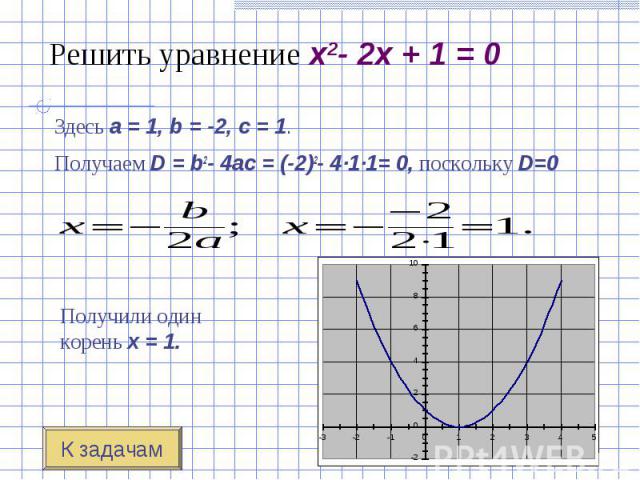
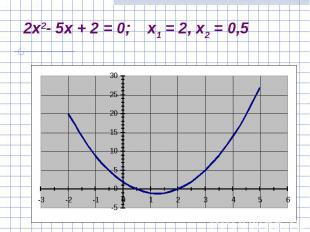
Решить уравнение 2x2- 5x + 2 = 0. Решить уравнение 2x2- 5x + 2 = 0. Решить уравнение 2x2- 3x + 5 = 0. Решить уравнение x2- 2x + 1 = 0.

Здесь a = 2, b = -5, c = 2. Здесь a = 2, b = -5, c = 2. Имеем D = b2- 4ac = (-5)2- 4 2 2 = 9. Так как D > 0, то уравнение имеет два корня. Найдем их по формуле

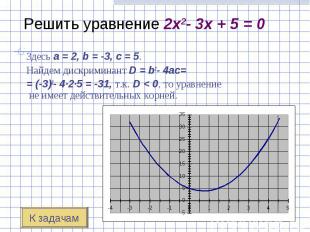
Здесь a = 2, b = -3, c = 5. Здесь a = 2, b = -3, c = 5. Найдем дискриминант D = b2- 4ac= = (-3)2- 4·2·5 = -31, т.к. D < 0, то уравнение не имеет действительных корней.  

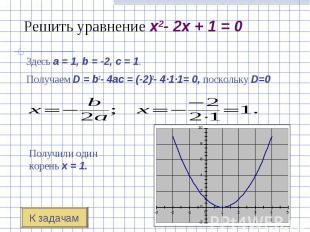
Здесь a = 1, b = -2, c = 1. Здесь a = 1, b = -2, c = 1. Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0

Определение квадратного уравнения Определение квадратного уравнения Определение приведенного квадратного уравнения Определение дискриминанта Формула корней квадратного уравнения Коэффициенты квадратного уравнения

Опр. 3. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1. Опр. 3. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1. х2 + bх + с = 0

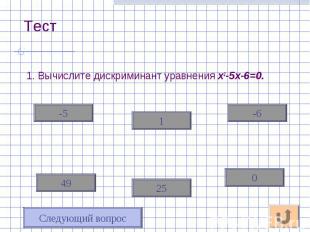
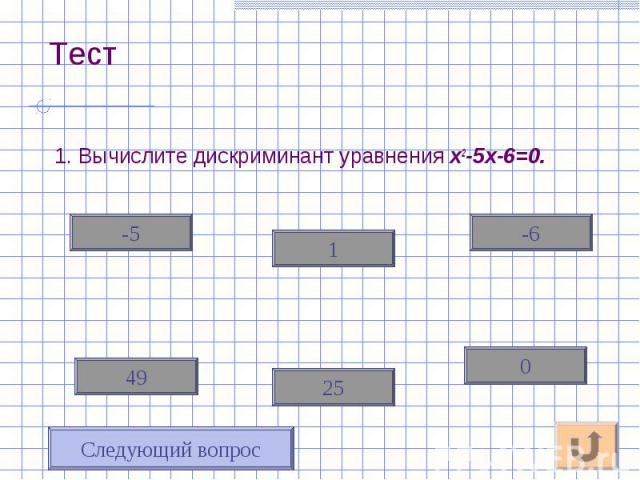
1. Вычислите дискриминант уравнения х2-5х-6=0. 1. Вычислите дискриминант уравнения х2-5х-6=0.

Вариант 1. Вариант 1. №1. Решите уравнения: а) х2+7х-44=0; б) 9у2+6у+1=0; в) –2t2+8t+2=0; г) а+3а2= -11. №2. При каких значениях х равны значения многочленов: (2-х)(2х+1) и (х-2)(х+2)?