Презентация на тему: Grafiki funkciy

Графики функции Подготовил: студент группы К-11 Лысенко Владислав

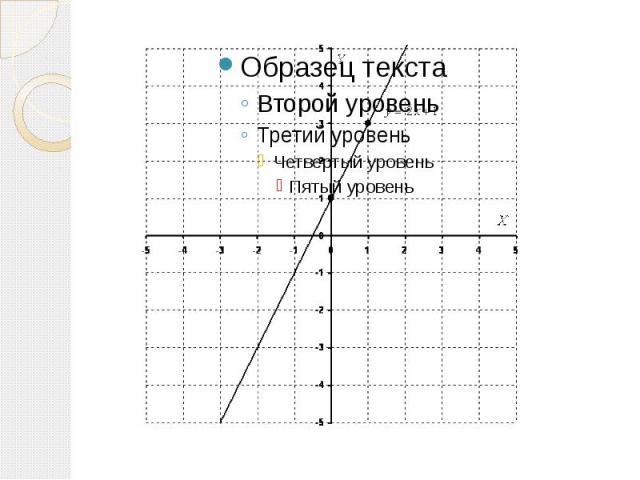
График линейной функции Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки. Пример 1 Построить график функции y=2x+1 . Найдем две точки. В качестве одной из точек выгодно выбрать ноль. Если  x=0, то y=2*0+1=1. Берем еще какую-нибудь точку, например, 1. Если x=1 , то  y=2*1+1=3.

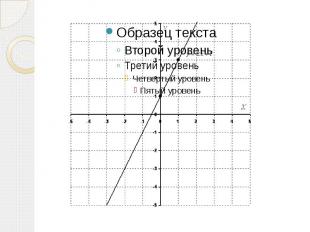
График квадратичной, кубической функции, график многочлена Область определения – любое действительное число (любое значение «икс»). Какую бы точку на оси Ox мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так:D(f)=R . Область определения любой функции стандартно обозначается через D(f) или D(y). Буква R обозначает множество действительных чисел или, проще говоря, «любое икс» .    

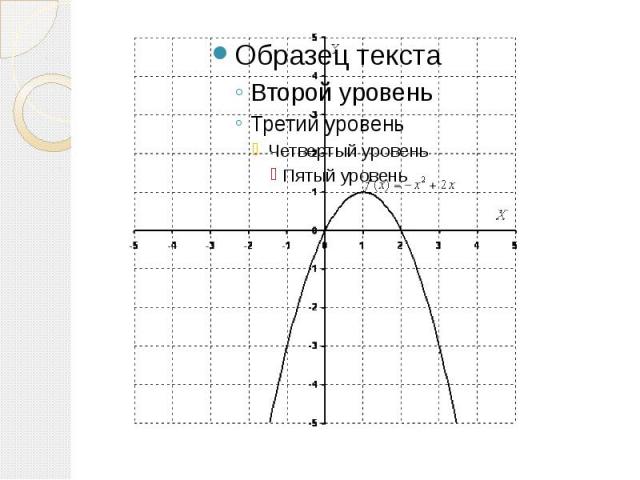
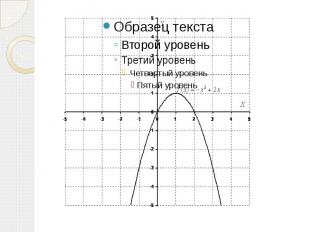
Пример 2 Пример 2 Построить график функции  y=-x^2+2x. Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю: f(x)’=(-x^2+2x)’=-2x+2=0. х=1 Pассчитываем соответствующее значение «игрек»: f(1)=(-1+2)=1. Вершина в точке (1;1). Теперь находим другие точки, при этом подставляя их в полученную производную.

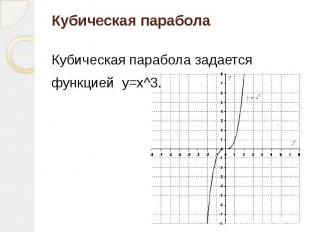
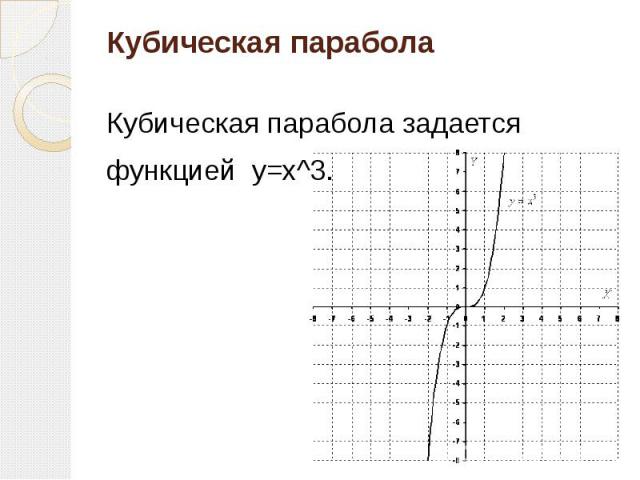
Кубическая парабола Кубическая парабола задается функцией  y=x^3.

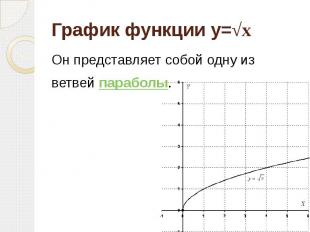
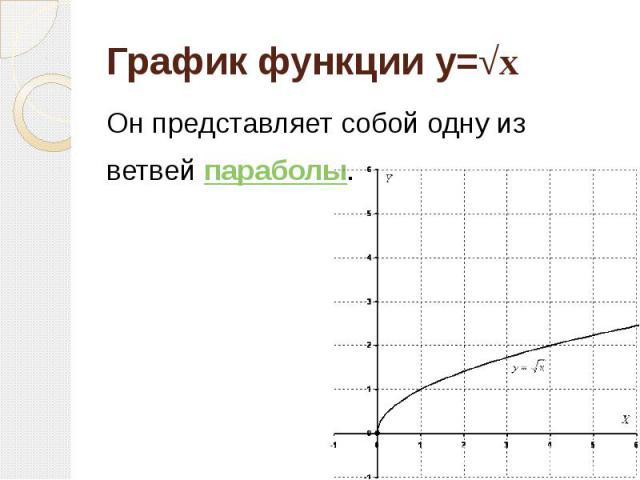
График функции y=√x Он представляет собой одну из ветвей параболы. 

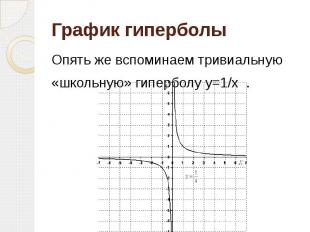
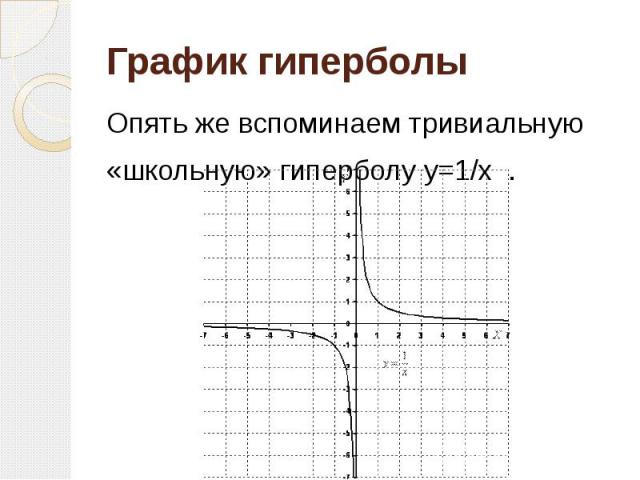
График гиперболы Опять же вспоминаем тривиальную «школьную» гиперболу y=1/x  .

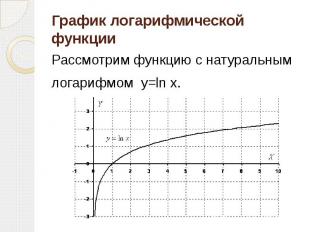
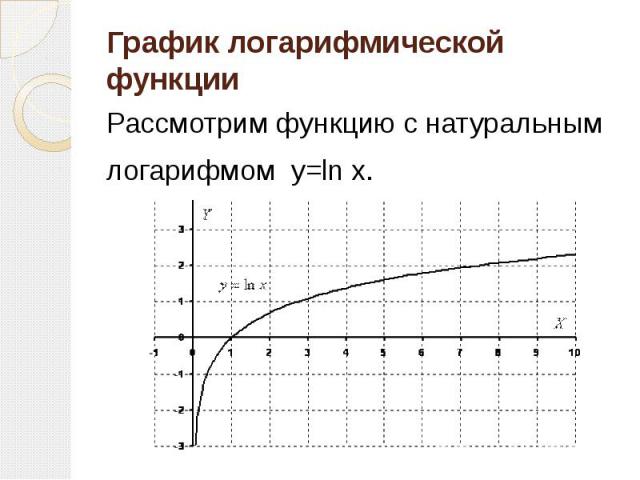
График логарифмической функции Рассмотрим функцию с натуральным логарифмом  y=ln x.

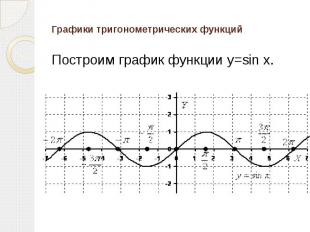
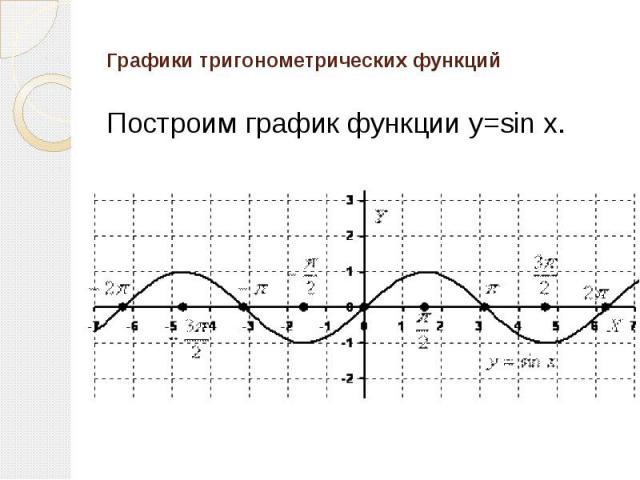
Графики тригонометрических функций Построим график функции y=sin x.

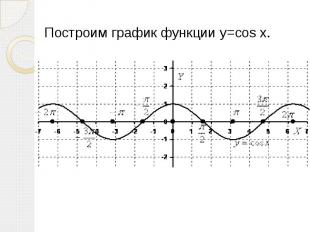
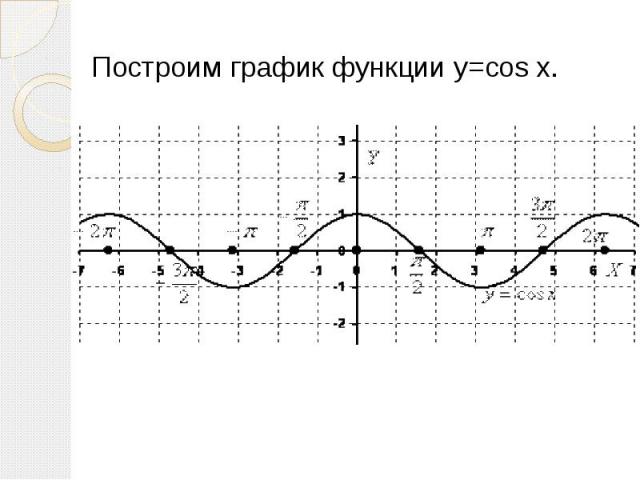
Построим график функции y=cos x. Построим график функции y=cos x.

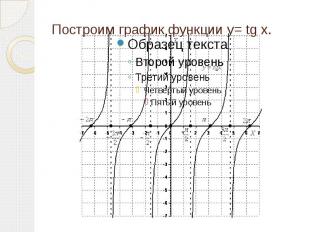
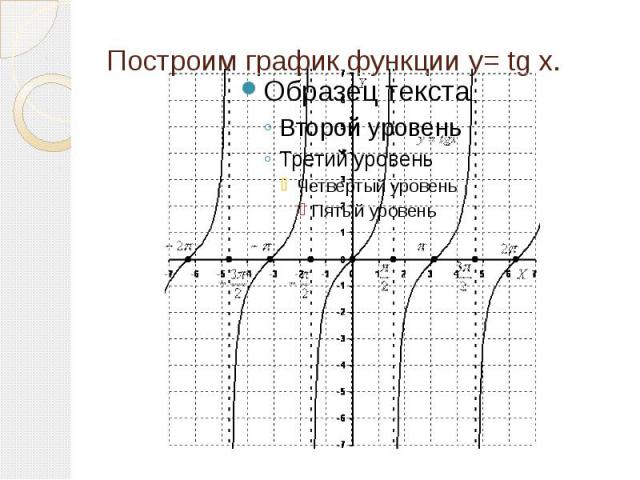
Построим график функции y= tg x.

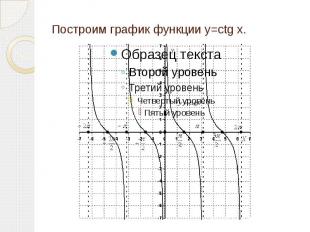
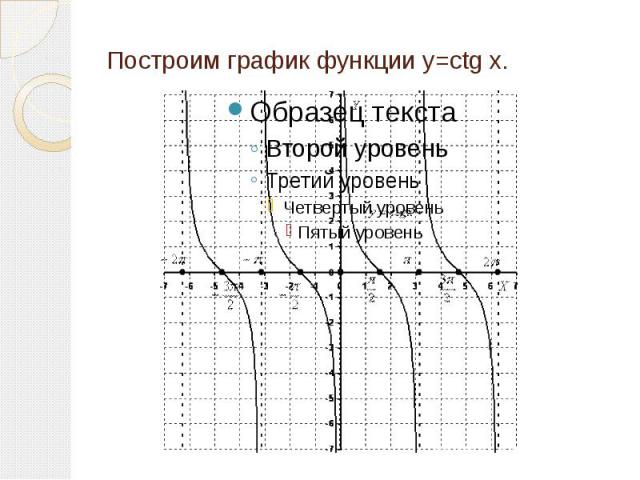
Построим график функции y=ctg x.