Презентация на тему: многогранники

ПІРАМІДИ Підготувала Маскаєва Анна, 11-А клас

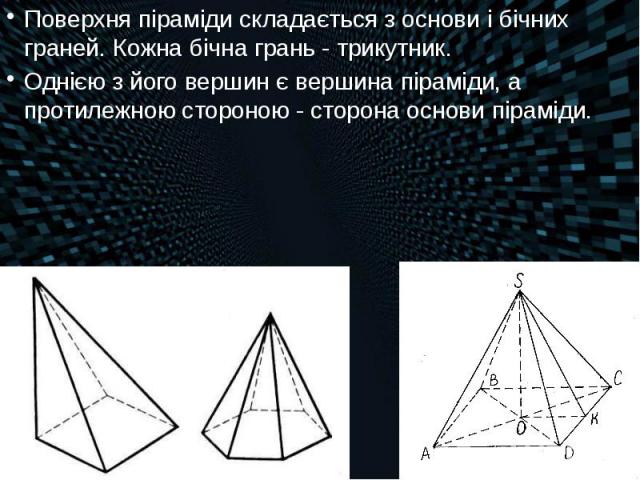
Піраміда — багатогранник, який складається з плоского багатокутника і точки (яка не лежить у площині основи) та всіх відрізків, що сполучають вершину піраміди з точками основи. Піраміда — багатогранник, який складається з плоского багатокутника і точки (яка не лежить у площині основи) та всіх відрізків, що сполучають вершину піраміди з точками основи. Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.

Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань - трикутник. Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань - трикутник. Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди.

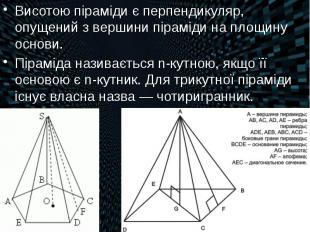
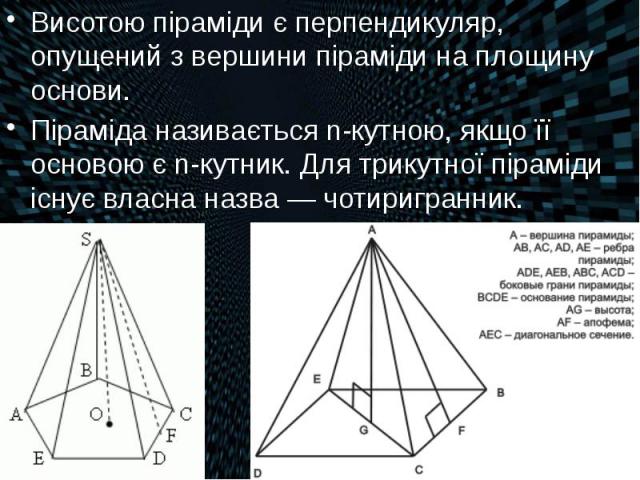
Висотою піраміди є перпендикуляр, опущений з вершини піраміди на площину основи. Висотою піраміди є перпендикуляр, опущений з вершини піраміди на площину основи. Піраміда називається n-кутною, якщо її основою є n-кутник. Для трикутної піраміди існує власна назва — чотиригранник.

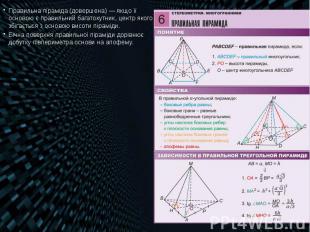
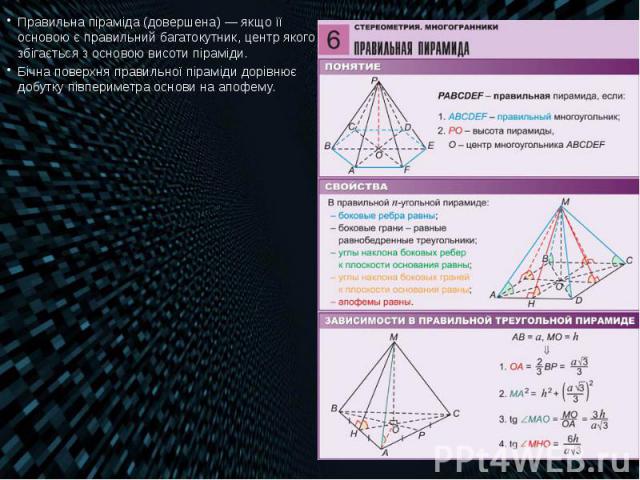
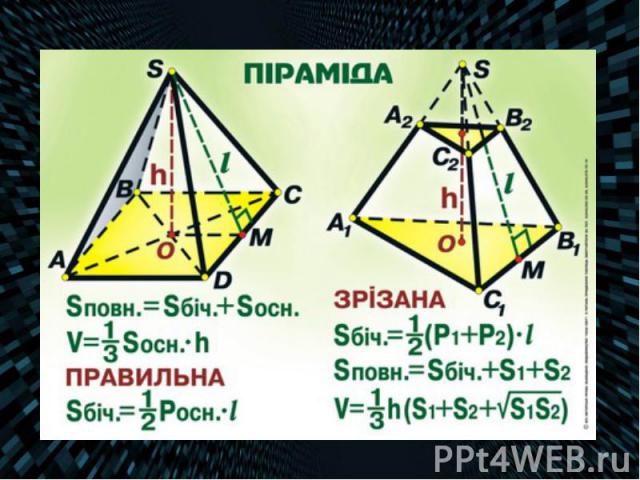
Правильна піраміда (довершена) — якщо її основою є правильний багатокутник, центр якого збігається з основою висоти піраміди. Правильна піраміда (довершена) — якщо її основою є правильний багатокутник, центр якого збігається з основою висоти піраміди. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

Вісь правильної піраміди — пряма, яка містить її висоту. У правильній піраміді бічні ребра рівні між собою, а бічні грані — рівні рівнобедрені трикутники. Вісь правильної піраміди — пряма, яка містить її висоту. У правильній піраміді бічні ребра рівні між собою, а бічні грані — рівні рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней.

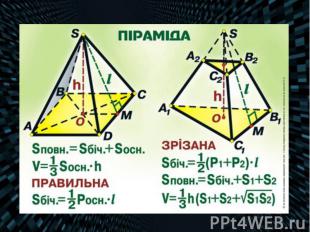
Площа бічної поверхні правильної піраміди дорівнює одній другій добутку периметра основи на апофему: Площа бічної поверхні правильної піраміди дорівнює одній другій добутку периметра основи на апофему: (тут Р — периметр, l — апофема, n — число сторін основи, b — бічне ребро, a — кут при вершині піраміди) Об'єм піраміди дорівнює одній третій добутку площі її основи на висоту :

Властивості правильної піраміди Такі три твердження є еквівалентними: бокові ребра піраміди рівні; бокові ребра піраміди нахилені до площини її основи під рівними кутами; проекція вершини піраміди на площину її основи співпадає із центром кола, описаного навколо основи.

Такі три твердження також є еквівалентними: Такі три твердження також є еквівалентними: вершина піраміди рівновіддалена від усіх сторін її основи; двогранні кути при основі піраміди рівні; вершина піраміди проеціюється до центру кола, вписаного в її основу.

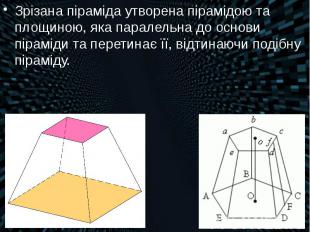
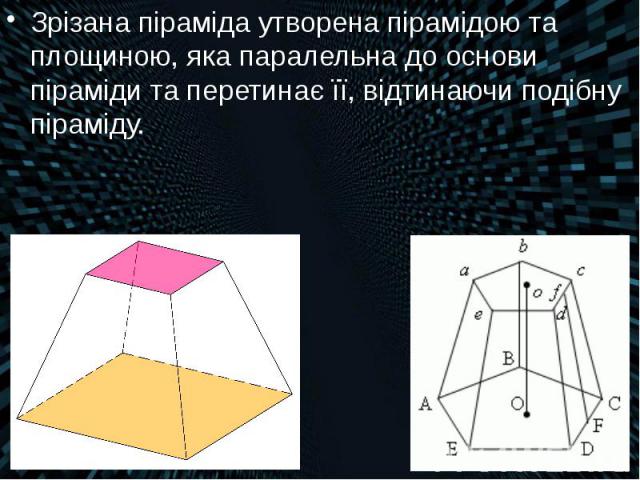
Зрізана піраміда утворена пірамідою та площиною, яка паралельна до основи піраміди та перетинає її, відтинаючи подібну піраміду. Зрізана піраміда утворена пірамідою та площиною, яка паралельна до основи піраміди та перетинає її, відтинаючи подібну піраміду.

Піраміди в нашому житті

Єгипетські піраміди Єгипетські піраміди

Трикутний кубік Рубіка Горщик для квітів Трикутний кубік Рубіка Горщик для квітів

Урна Вуличний ліхтар Урна Вуличний ліхтар

Дитяча піраміда Дитяча піраміда