Презентация на тему: Многогранники

Многогранники

Многогранник, точнее трёхмерный многогранник — совокупность конечного числа плоских многоугольников в трёхмерном евклидовом пространстве, такая, что: Многогранник, точнее трёхмерный многогранник — совокупность конечного числа плоских многоугольников в трёхмерном евклидовом пространстве, такая, что: каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым (по этой стороне); связность: от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого, в свою очередь, к смежному с ним, и т. д. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника

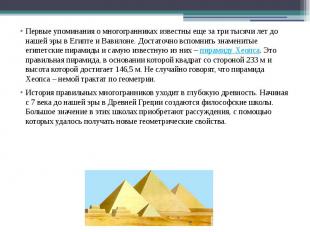
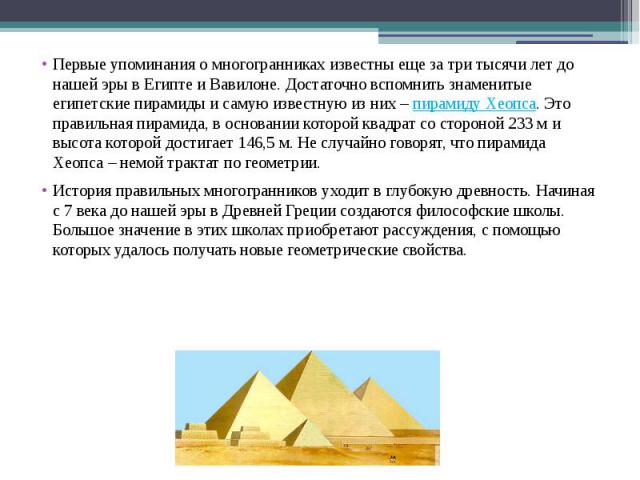
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии. Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии. История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

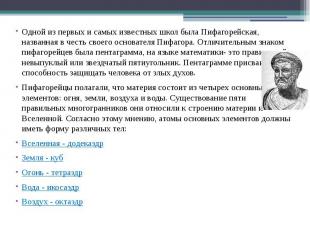
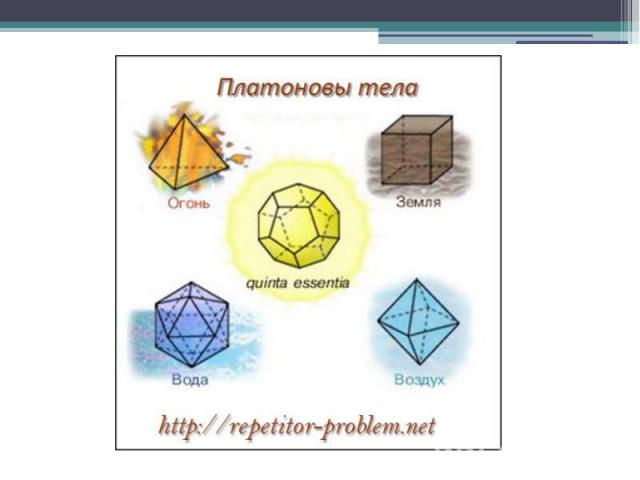
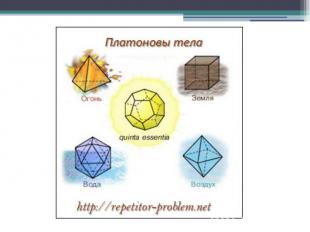
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов. Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел: Вселенная - додекаэдр Земля - куб Огонь - тетраэдр Вода - икосаэдр Воздух - октаэдр

Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами. Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, впервые перечислившего их в недошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа.

Правильные многогранники Имеется несколько эквивалентных определений правильных многогранников. Одно из них звучит так: многогранник называется правильным, если существуют три концентрические сферы, одна из которых касается всех граней многогранника, другая касается всех его ребер и третья содержит все его вершины. Это определение напоминает одно из возможных определений правильного многоугольника: многоугольник называется правильным, если он вписан в некоторую окружность и описан около другой окружности, причем эти окружности концентричны. Другое определение: правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны. Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платоновыми телами (хотя известны они были задолго до Платона).

Существует всего 5 видов правильных многогранников: Куб (гексаэдр) Тетраэдр Октаэдр Икосаэдр Додекаэдр

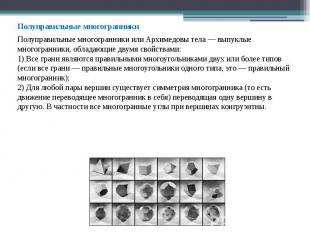
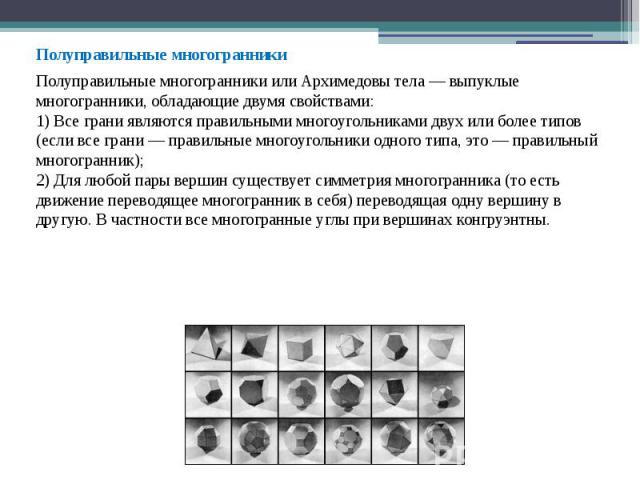
Полуправильные многогранники Полуправильные многогранники Полуправильные многогранники или Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами:  1) Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник);  2) Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности все многогранные углы при вершинах конгруэнтны.

Существует 13 полуправильных многогранников: Существует 13 полуправильных многогранников: Кубооктаэдр Икосододекаэдр Усеченный тетраэдр Усечённый куб Усечённый октаэдр Усечённый додекаэдр Усечённый икосаэдр Ромбокубооктаэдр Ромбоусечённый кубоктаэдр Ромбоикосододекаэдр Ромбоусечённый икосододекаэдр Курносый куб Курносый додекаэдр

Звездчатые многогранники Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

Многогранники в природе Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.

Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды. Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.

Многогранники в архитектуре Использовать многогранники в архитектуре люди стали очень давно, еще до новой эры. И по мере роста строительного мастерства в мире появлялись новые шедевры, основанные на сложных геометрических фигурах. Наша Национальная библиотека — одна из них.

Благодаря своей нетривиальной архитектуре Национальная библиотека попадала в самые различные рейтинги — от самых необычных зданий мира, до — не поверите! — самых уродливых. А все из-за формы книгохранилища — ромбокубооктаэдра.

Повторить в архитектуре сложные многогранники (особенно, архимедовы тела — к которым, в том числе, относится и ромбокубооктаэдр) действительно нелегко. И если случается, то в меньшем масштабе, чем Нацбиблиотека, и усеченной форме.

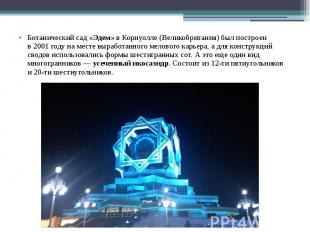
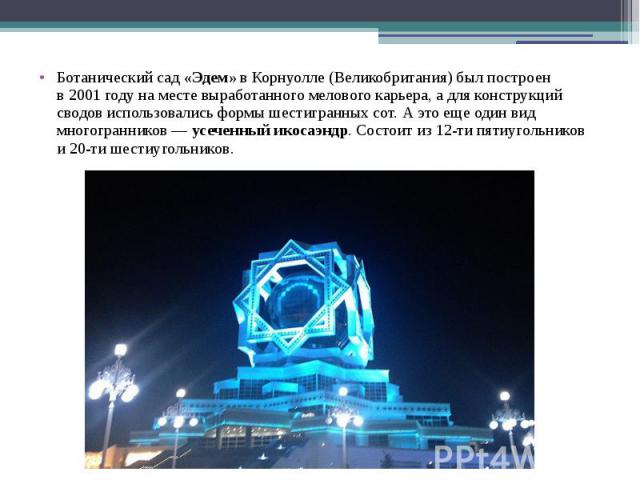
Ботанический сад «Эдем» в Корнуолле (Великобритания) был построен в 2001 году на месте выработанного мелового карьера, а для конструкций сводов использовались формы шестигранных сот. А это еще один вид многогранников — усеченный икосаэндр. Состоит из 12-ти пятиугольников и 20-ти шестиугольников.

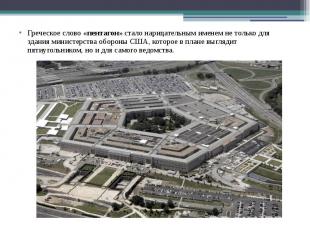
Греческое слово «пентагон» стало нарицательным именем не только для здания министерства обороны США, которое в плане выглядит пятиугольником, но и для самого ведомства.

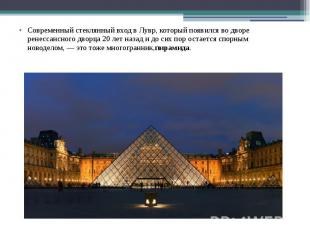
Современный стеклянный вход в Лувр, который появился во дворе ренессансного дворца 20 лет назад и до сих пор остается спорным новоделом, — это тоже многогранник,пирамида.

Вот так выглядит здание публичной библиотеки в Сиэтле (США).

Подготовила: Громова Валерия 10 «Б» класс