Презентация на тему: Аксиомы планиметрии

Аксиомы планиметрии

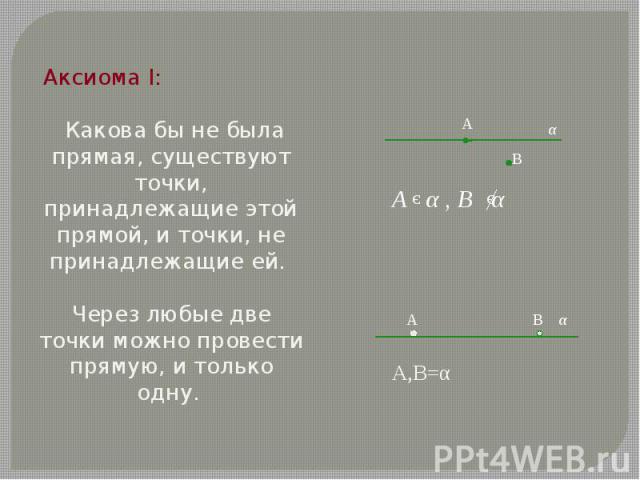
Аксиома I: Аксиома I: Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

Аксиома II: Аксиома II: Из трёх точек на прямой одна и только одна лежит между двумя другими.

Аксиома III: Аксиома III: Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Аксиома IV: Аксиома IV: Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме, градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиома V: Аксиома V: На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.

Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости. Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости. Основными геометрическими фигурами на плоскости являются точка и прямая.

Спасибо за просмотр!