Презентация на тему: Формула объёма шара

Урок по теме: «Объем шара». 11-й класс Махмутова Фануза Фаиковна, учитель математики высшей категории. МБОУ «Новошешминская гимназия Новошешминского муниципольного района РТ» 5klass.net

Цель урока: вывести формулу объема шара; обобщить и систематизировать знания по теме «Тела вращения» Ход урока: I. Организационный момент. II. Актуализация опорных знаний. Устная работа 2) Презентации решений задач с ЕГЭ III. Изучение новой темы Теорема IV.Формирование умений и навыков учащихся. Проблемная задача Задача Архимеда Задачи из ЕГЭ(В9) V. Итог урока. Домашнее задание.

Соотнесите название фигуры и формулу объема и площади поверхности тел. 1.Цилиндр 2.Конус 3.Усеченный конус 4. Шар

Название фигуры Формула Цилиндр Конус Усеченный конус Шар

Задачи В 11 (ЕГЭ)

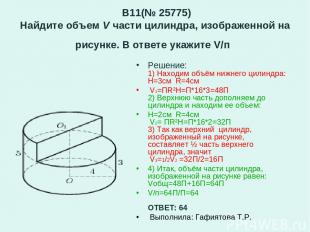
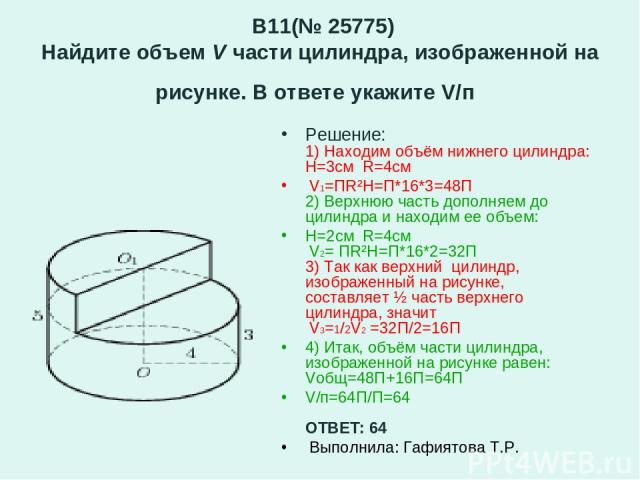
B11(№ 25775) Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/п Решение: 1) Находим объём нижнего цилиндра: H=3см R=4см V1=ПR²H=П*16*3=48П 2) Верхнюю часть дополняем до цилиндра и находим ее объем: Н=2см R=4см V2= ПR²H=П*16*2=32П 3) Так как верхний цилиндр, изображенный на рисунке, составляет ½ часть верхнего цилиндра, значит V3=1/2V2 =32П/2=16П 4) Итак, объём части цилиндра, изображенной на рисунке равен: Vобщ=48П+16П=64П V/п=64П/П=64 ОТВЕТ: 64 Выполнила: Гафиятова Т.Р.

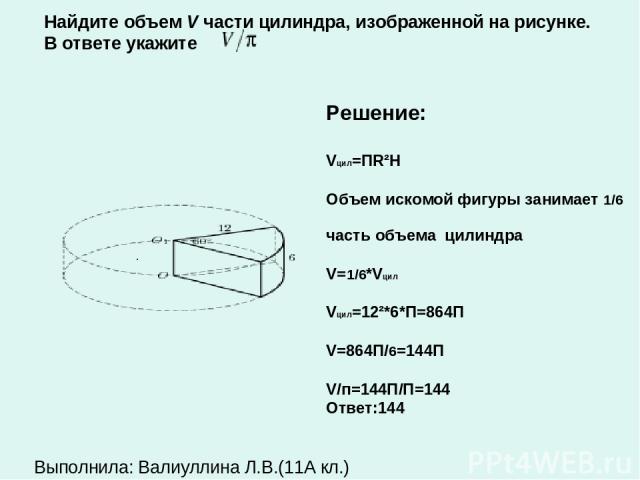
. Решение: Vцил=ПR²H Объем искомой фигуры занимает 1/6 часть объема цилиндра V=1/6*Vцил Vцил=12²*6*П=864П V=864П/6=144П V/п=144П/П=144 Ответ:144 Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите Выполнила: Валиуллина Л.В.(11А кл.)

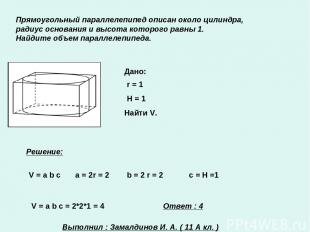
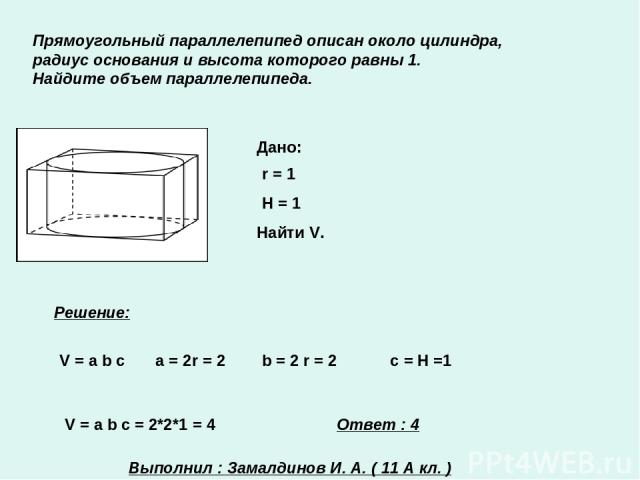
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. Дано: r = 1 H = 1 Найти V. Решение: V = a b c a = 2r = 2 b = 2 r = 2 с = Н =1 V = a b c = 2*2*1 = 4 Ответ : 4 Выполнил : Замалдинов И. А. ( 11 А кл. )

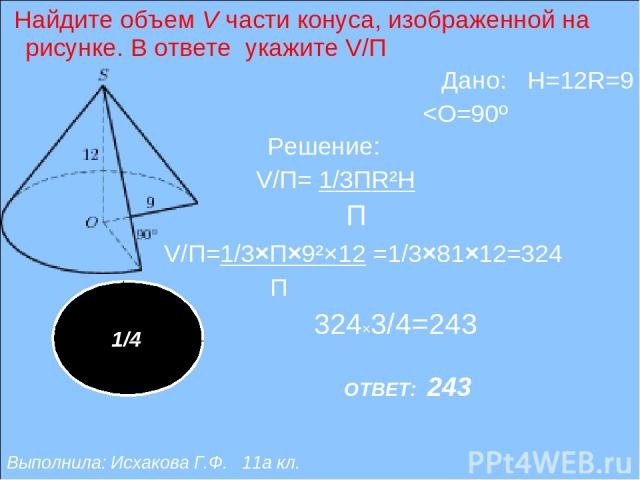
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/П Дано: H=12R=9

B11 (№ 25739) Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите R=3;H=4. Решение: Vц = π R²H=π·3²·4=36π. Так как объем искомой фигуры занимает ¼ часть целого цилиндра, ее объем будет равен: 36π/4=9π По условию задачи объем искомой фигуры будет равен: 9π/π=9. Ответ:9 Выполнила: Арсланова Л.И. (11А кл)

Решение: . V/ Ответ:1125 Выполнила: Галиуллина М.Ф. (11Акл)

Сфера (шар) О – центр сферы (шара) A;F – полюсы сферы (шара) ОВ – радиус сферы (шара) BC – диаметр сферы (шара) О А R C F Шар – множество точек пространства, находящихся на расстоянии не большем R от данной точки. Фигура, полученная в результате вращения полукруга вокруг диаметра, называется шаром. B

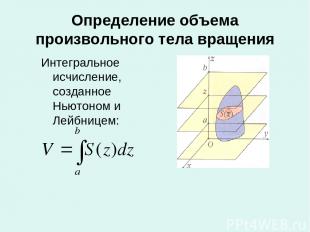
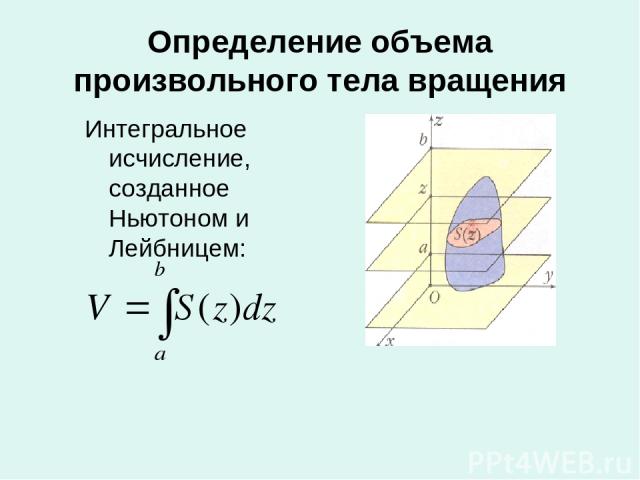
Определение объема произвольного тела вращения Интегральное исчисление, созданное Ньютоном и Лейбницем:

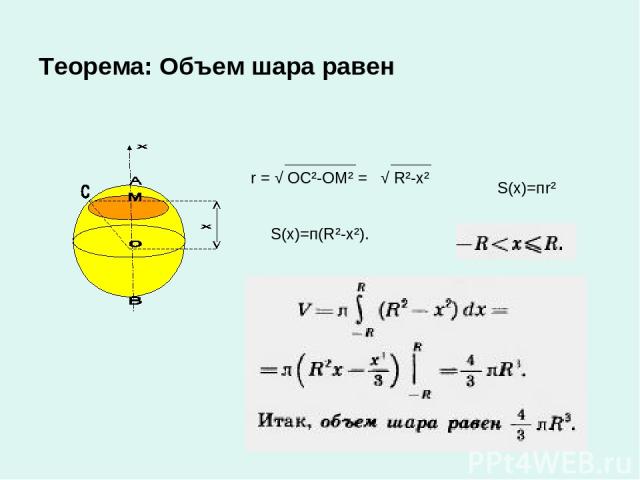
Теорема: Объем шара равен r = √ ОС²-ОМ² = √ R²-x² S(x)=пr² S(x)=п(R²-x²).

ПРОБЛЕМНАЯ ЗАДАЧА При уличной торговле арбузами весы отсутствовали. Однако, выход был найден: арбуз диаметром 3 дм приравнивали по стоимости к трём арбузам диаметром 1 дм. Что вы возьмете? Правы ли были продавцы? = + +

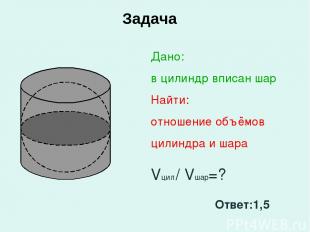
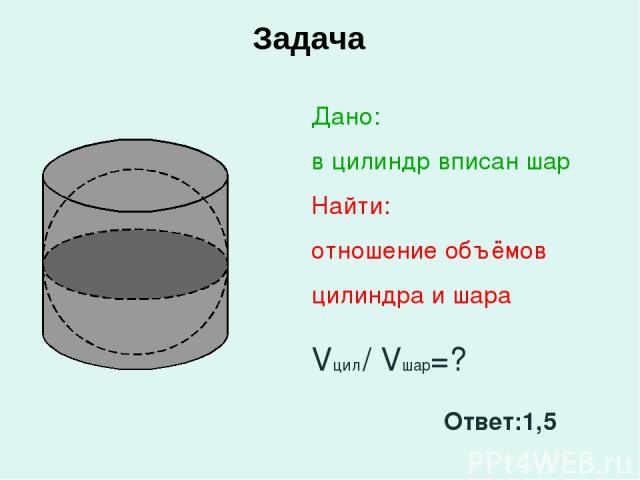
Задача Дано: в цилиндр вписан шар Найти: отношение объёмов цилиндра и шара Vцил / Vшар=? Ответ:1,5

Архимед считал, что объем шара в 1,5 раза меньше объема описанного около него цилиндра и что также относятся поверхности этих тел.

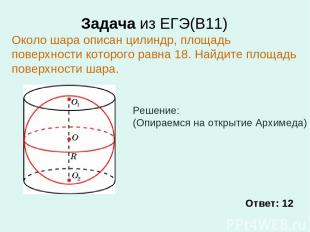
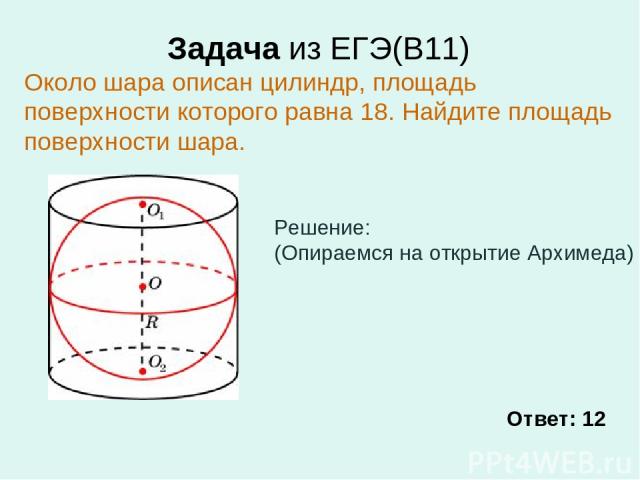
Задача из ЕГЭ(В11) Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара. Ответ: 12 Решение: (Опираемся на открытие Архимеда)

Площадь поверхности шара уменьшили 9 раз. Во сколько раз уменьшился объем шара? Решение: Пусть радиус первого шара R, уменьшенного r. Поверхность шара S1 = 4пR², стала S2 = 4пR²/9 = 4п (R/3)² = 4пr² Видим, что r =R/3, т.е. радиус уменьшился в 3 раза. Объем V1= 4/3 ПR³, а объем V2= 4/3 пr³ = =4/3 п(R/3)³ =4/3 пR³ /27 = V1 / 27 Ответ:27 Задача из ЕГЭ(В11)

Использованные интернет ресурсы http://festival.1september.ru/articles/559546/ http://www.proshkolu.ru/org/107-360/file/491954/ http://sport.teem.ru/images/shaiba.jpg http://www.alleng.ru/d/math/math394.htm http://alexlarin.narod.ru/ege.html http://www.varson.ru/geometr_9.html