Презентация на тему: Измерение длин отрезков

Измерение длин отрезков Урок № 7

I. Математический диктант

Вариант 1 1. Из трех точек на прямой только … 2. Отрезком называется … 3. Луч обозначается … 4. Отрезок AB является суммой отрезков AC и CB и обозначается … 5. Если два отрезка равны третьему, то … 6. Умножить отрезок AB на натуральное число n, значит, … Вариант 2 1. Каждая точка на прямой разбивает эту прямую на … 2. Лучом называется … 3. Отрезок обозначается … 4. Отрезок AC является разностью отрезков AB и CB и обозначается … 5. На любом луче от его начала можно отложить … 6. Разделить отрезок AB на натуральное число n значит, …

Вариант 1 1.лежит между двумя другими 2.часть прямой состоящая из 2 данных точек и всех точек лежащих между ними. 3.AC+CB 4.То они равны 5.Его надо сложить с собой n раз Вариант 2 1.На две части 2.Часть прямой, сотоящая из точки этой прямой и всех точек, лежащих от нее по одну сторону. 3.AB-CB 4.Один отрезок, равный данному. 5.Деление отрезка на n равных частей

Лабораторная работа. Возьмем отрезок OE (10 клеток) и назовем его единичным. 2. Теперь возьмем отрезок AB (20 клеток). Сколько раз единичный отрезок OE укладывается в отрезке AB? Далее возьмем отрезок CD (30 клеток). Сколько раз единичный отрезок OE укладывается в отрезке CD? Полученные числа 2 и 3 являются соответственно длинами отрезков AB и CD. Можно ввести специальное обозначение для длины отрезка, а именно, |AB|=2, |CD|=3.

3. Возьмем отрезок MN (11 клеток). Единичный отрезок OE укладывается в данном отрезке один раз и еще остается одна клетка, которая в данном случае равна единичного отрезка. Следовательно, |MN|=1,1. 4. Определим длину отрезка GH (23 клетки) и KL (5 клеток). |GH|=2,3; |KL|=0,5. Вывод. Измерение длины отрезка основано на сравнении его с отрезком, длина которого принимается за единицу (единичный отрезок).

Длина отрезка – это положительное число, показывающее сколько раз единичный отрезок и его части укладываются в этом отрезке. Единичный отрезок можно разбивать не только на 10, но и на другое число частей. Так, если единичный отрезок разбит на q равных частей и одна такая часть укладывается в отрезке АВ ровно р раз, то длина отрезка АВ считается равной дроби 8/3 . На рисунке q = 3, р = 8. Длину отрезка AB называют также расстоянием между точками A и B. Иногда, под расстоянием между точками A и B будем понимать сам отрезок AB. Длину отрезка АВ будем обозначать так же как и сам отрезок, АВ.

Вопросы - Возьмем два равных отрезка AB и A1B1. Что можно сказать об их длинах? - Дан отрезок AC, который является суммой отрезков AB и BC. Что можно сказать о длине суммы этих отрезков?

Свойства длины отрезка : Свойство 1. Длины равных отрезков равны. Свойство 2. Длина суммы отрезков равна сумме их длин.

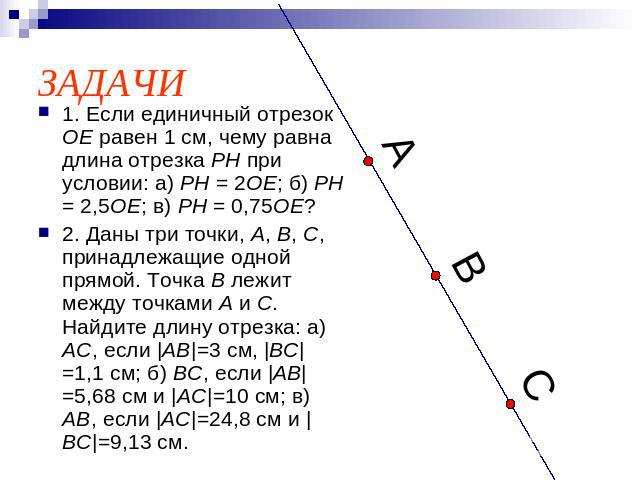
ЗАДАЧИ 1. Если единичный отрезок OE равен 1 см, чему равна длина отрезка PH при условии: а) PH = 2OE; б) PH = 2,5OE; в) PH = 0,75OE? 2. Даны три точки, A, B, C, принадлежащие одной прямой. Точка B лежит между точками A и C. Найдите длину отрезка: а) AC, если |AB|=3 см, |BC|=1,1 см; б) BC, если |AB|=5,68 см и |AC|=10 см; в) AB, если |AC|=24,8 см и |BC|=9,13 см.

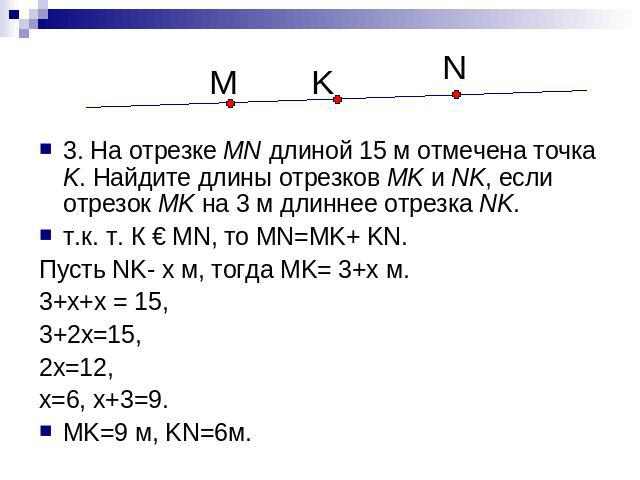
3. На отрезке MN длиной 15 м отмечена точка K. Найдите длины отрезков MK и NK, если отрезок MK на 3 м длиннее отрезка NK. т.к. т. К € MN, то MN=MK+ KN. Пусть NK- x м, тогда MK= 3+x м. 3+x+x = 15, 3+2x=15, 2x=12, x=6, x+3=9. MK=9 м, KN=6м.

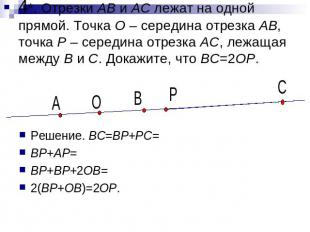
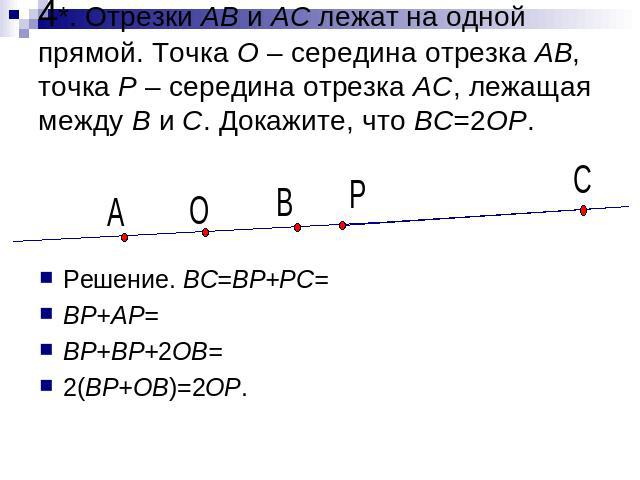
4*. Отрезки AB и AC лежат на одной прямой. Точка O – середина отрезка AB, точка P – середина отрезка AC, лежащая между B и C. Докажите, что BC=2OP. Решение. BC=BP+PC= BP+AP= BP+BP+2OB= 2(BP+OB)=2OP.

Домашнее задание § 3, выучить теорию № 3,9,14,17, Отрезки AB и AC лежат на одной прямой. Точка O – середина отрезка AB, точка P – середина отрезка AC и точка C лежит между точками P и O. Докажите, что BC=2OP. 3*. Индивидуальное задание. Исторический экскурс об единицах измерения длины (см. рубрику «Исторические сведения» из п. 3 учебника).