Презентация на тему: Законы булевой алгебры и упрощение логических выражений

Тема: "Законы булевой алгебры и упрощение логических выражений" Учитель информатикиГБОУ СОШ №1226 Качулина Ю. Аг. Москва

Повторение пройденного материала Что изучает логика?Какие формы мышления существуют?Что такое сложное высказывание? Сколько Вы знаете базовых логических операций? Перечислите названия базовых логических операцийДля чего нужна таблица истинности?

Поставьте в соответствие логические операции и знаки для их обозначения ИнверсияКонъюнкцияДизъюнкцияИмпликацияЭквивалентность

Закрепление пройденного материала

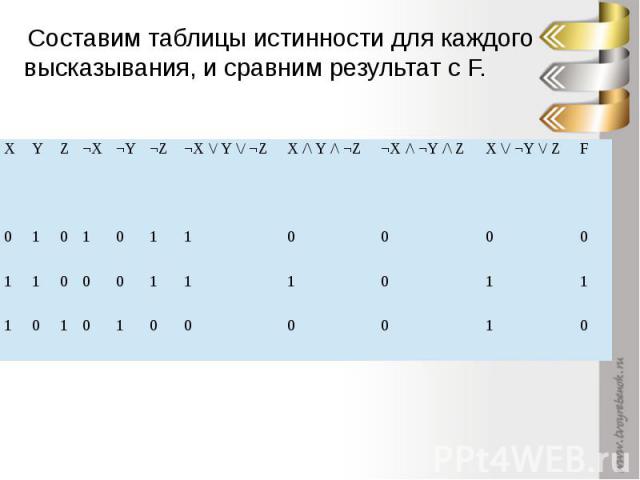
A11. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F?

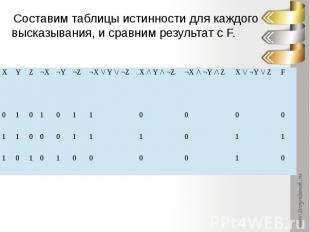
Составим таблицы истинности для каждого высказывания, и сравним результат с F.

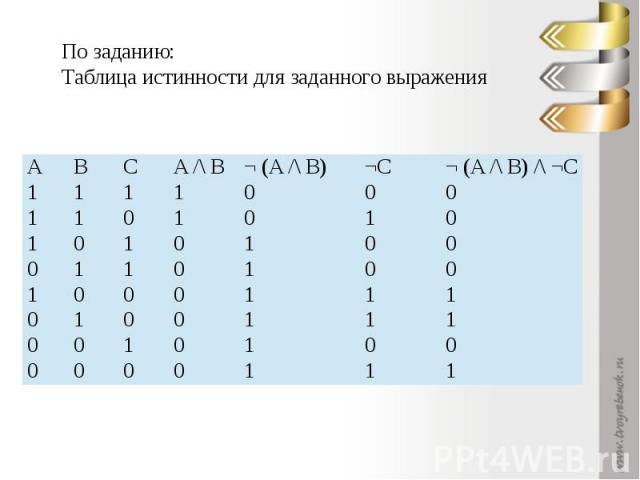
Какое логическое выражение равносильно выражению ¬ (A /\ B) /\ ¬C?

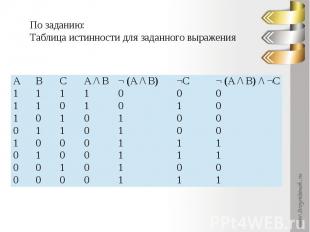
По заданию: Таблица истинности для заданного выражения

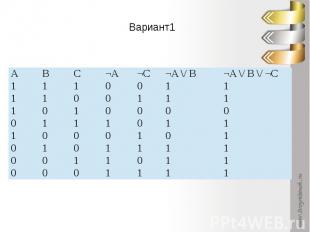
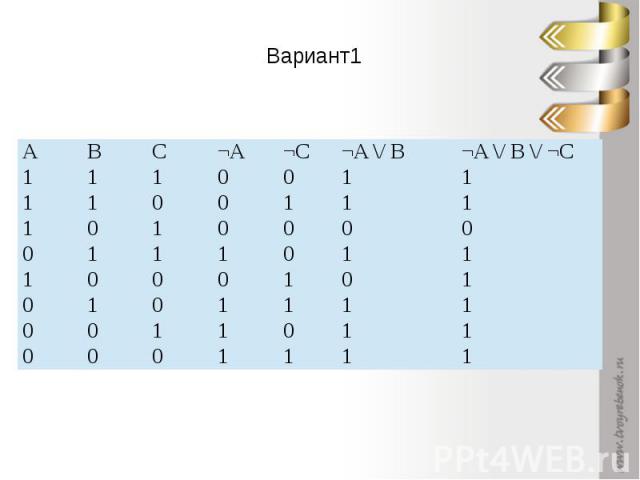
Вариант1

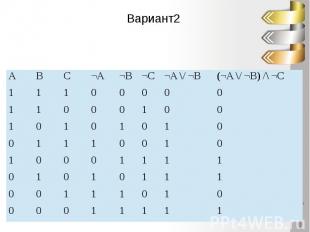
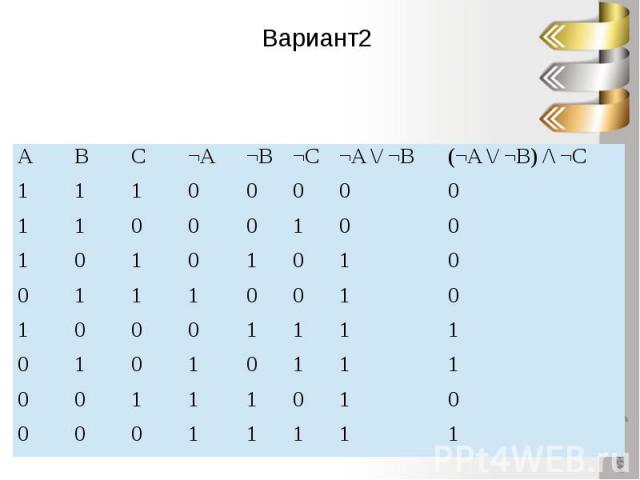
Вариант2

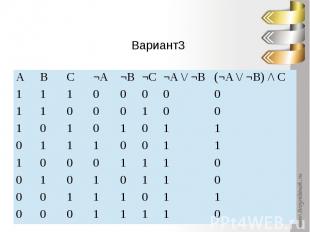
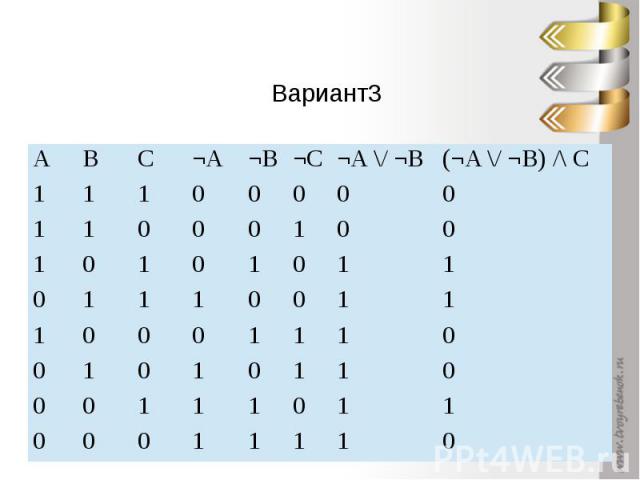
Вариант3

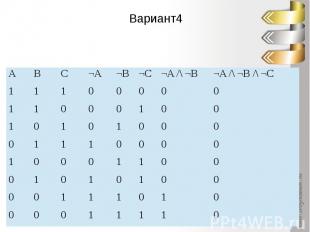
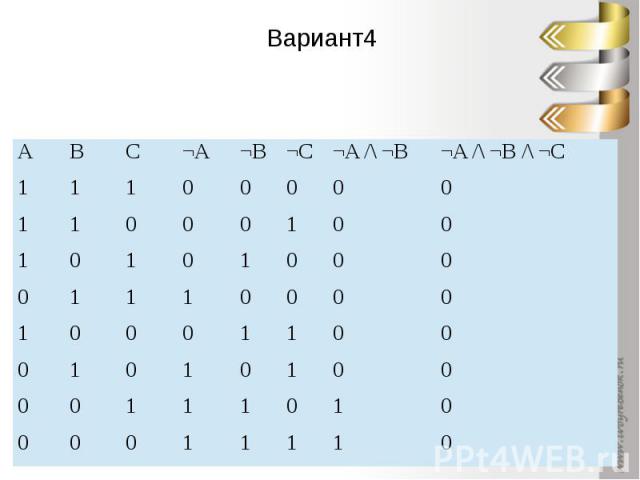
Вариант4

Сравним таблицы истинностиОтвет. 2

Показалось ли вам решение этой задачи слишком громоздким? Я, например, сразу могу сказать вам ответ этой задачи, не строя таблицы истинности. Как вы думаете, каким образом? Существуют специальные законы преобразования выражений и сегодня мы с вами рассмотрим их.

Изучение нового материала

Логические законы:1. Независимость от перестановки мест (коммутативность) A v B = B v A A ^ B = B ^ A 2. Независимость от порядка выполнения однотипных действий (ассоциативность) (A v B) v С = A v (B v С) (A ^ B) ^ С= A ^ (B ^ С)

3. Распределительный закон относительно логического умножения и сложения (дистрибутивность) Распределение относительно логического умножения: (А v В) ^ C = (A ^ C) v (В ^ C). Вспомним правила раскрытия скобок в алгебре, ведь недаром операции конъюнкции и дизъюнкции называют логическим умножением и сложением. И наоборот: (A & B) v (В & C) = В & (А v C). Похоже на вынесение общего множителя за скобки в алгебре. Распределительный закон относительно логического умножения полностью повторяет аналогичный закон алгебры.

4. Отсутствие степеней и коэффициентов (идемпотентность) А v А = А А ^ А = А Если высказывание А ложно (0), то результат 0 v 0, а также 0 ^ 0 – ложь; если высказывание А истинно (1), то результат 1 v 1, а также 1 ^ 1 - истина

5. Двойное отрицание (инволюция) ¬ (¬ А) = А

6. Закон константА v 1 =1 (всегда истина) А ^1 = А А v 0 = А А ^ 0 = 0 (всегда ложь)

7. Закон исключенного третьего А v ¬ А = 1 (всегда истина) 8. Закон противоречия А ^ ¬ А = 0 (всегда ложь) В этом выражении что-то одно (либо А, либо ¬ А) ложно, поэтому результат логического умножения – ложь.

9. Законы де Моргана ¬ (А ^ В) = ¬ А v ¬ В ¬ (А v В) = ¬ А ^ ¬ В

10. Поглощение А v (А ^ В) = А А ^ (А v В) = А 11. Поглощение отрицания А v ( ¬ А ^ В) = А v В А ^ ( ¬ А v В) = А ^ В

Существуют формулы замены операций импликация и эквиваленция с использованием только операций отрицания, дизъюнкции и конъюнкции. Так, вместо операции импликации можно использовать следующее тождественное выражение: A → B = не A V B Для замены операции эквивалентности существует два выражения: A равносильно B = (A * B) V (не A * не B) A равносильно B = (A V не B) * (не A V B)

Закрепление изученного: упрощение логических выражений 1) Упростить логическое выражение. _______________ _____ F = (A v B) → (B v C)Заменим операцию импликация на

Используются законы де Моргана, закон двойного отрицания, распределительный закон

Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее:Если не будет ветра, то будет пасмурная погода без дождя.Если будет дождь, то будет пасмурно и без ветра.Если будет пасмурная погода, то будет дождь и не будет ветра.Так какая же погода будет завтра? Решим эту задачу средствами алгебры логики.Решение:а) Выделим простые высказывания и запишем их через переменные: A – «Ветра нет» B – «Пасмурно» С – «Дождь»

Закрепление нового материала

б) Запишем логические функции (сложные высказывания) через введенные переменные:1. Если не будет ветра, то будет пасмурная погода без дождя: __ A → B & C2. Если будет дождь, то будет пасмурно и без ветра: С → B & A 3. Если будет пасмурная погода, то будет дождь и не будет ветра B → C & Aв) Запишем произведение указанных функций: _ F=(A→ B & C) & (C→B & A) & (B→ C & A)

г) Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия): _F=(A→ B & C) & (C→B & A) & (B→ C & A) _ _ _ _ = (A v B & C) & (C v B&A) & (B v C&A) = _ _ _ _= (A v B & C) & (B v C&A) & (C v B&A) = _ _ _ _ _ _ = (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)= _ _ _ _ _ _ _= A & B &(C v B&A) =A&B&C v A&B&B&A = _ _ _ = A&B&C

д) Приравняем результат единице, т.е. наше выражение должно быть истинным: _ _ _ F = A & B & C = 1е) Проанализируем результат:Логическое произведение равно 1, если каждый множитель равен 1. Поэтому: _ _ _ A = 1; B = 1; C = 1;Значит: A = 0; B = 0; C = 0;Ответ: погода будет ясная, без дождя, но ветреная.

Подведение итогов урока Какой способ решения легче?Что было легко, а что трудно? Что было интересно, а что не затронуло? Что нового для себя вы узнали, чему научились? Какие умения Вы приобрели ?

Домашнее задание. Выучить законы алгебры-логики. Выполнить задание: Используя полученные на уроке знанияКакое логическое выражение равносильно выражению ?