Презентация на тему: Приключение Алгебры в стране Геометрия

Приключение Алгебры в стране Геометрия Способы представления иррациональных чисел

“Все известные вещи имеют число. Без этого ничего нельзя было бы ни мыслить, ни знать”Пифагор

Легенда Рассказывают, что великий геометр, открыв НЕСОИЗМЕРИМОСТЬ сторон квадрата и его диагонали, увидел в том божественный знак, - и поспешил принести в жертву олимпийцам сотню быков. Пифагора легко понять - ведь он воочию узрел Бесконечность.

Представления чисел пифагорейцами

Главным открытием Пифагора был прямоугольный равнобедренный треугольник, возникающий в квадрате, где проведена диагональ.

Что такое НЕСОИЗМЕРИМОСТЬ? Нетрудно сказать: какую бы часть стороны квадрата мы ни взяли - половину, четверть, треть и т.п. - ни одна из этих мер не уложится на диагонали целое число раз, всегда будет «остаток». Так в математике появились иррациональные числа, в десятичной системе мы выражаем их в виде бесконечных дробей.

Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами Первая фигура — квадрат — одна из простейших фигур, имеющаяравные стороны. Она является основной формой в ранней архитектуре Древнего Египта Вторая фигура — прямоугольник с отношением сторон, равным отношению стороны квадрата к его диагонали.

Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами Третья фигура – прямоугольник с длинами сторон а и √3∙a Четвёртая фигура представляет собой прямоугольник, составленный из двух квадратов, длина сторон которого а и 2а

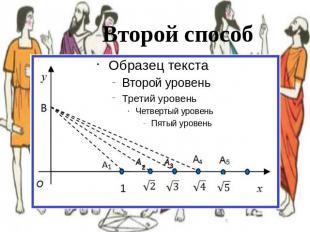
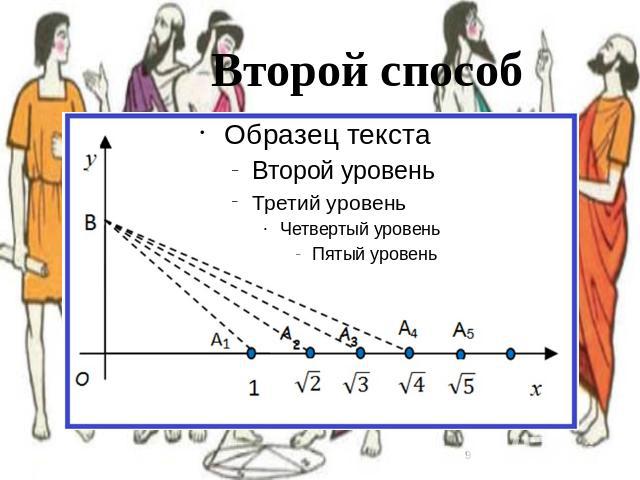
Второй способ

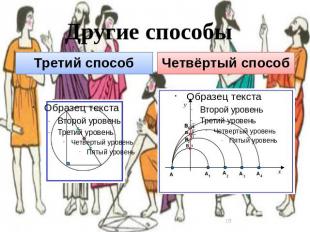
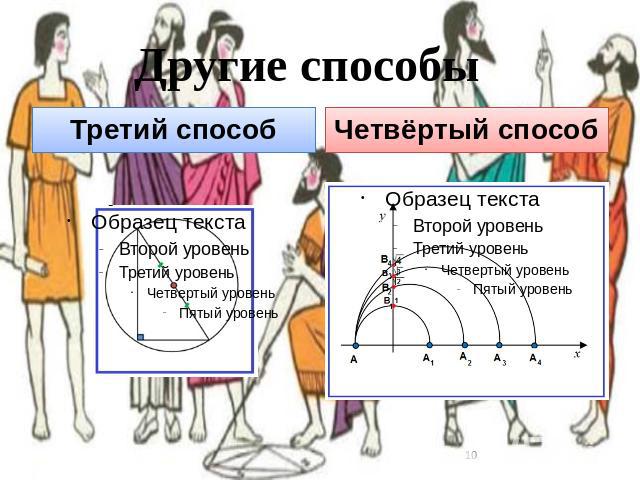
Третий способ Третий способ Четвёртый способ

Пропорции в древнем Египте Система квадратов и его производных стала применяться ещё в древности. По этим пропорциям построен один из ранних египетских памятников – предполагаемая гробница фараона МЕНЕСА в Негаде, относящаяся к I династии (рис.9).

Практическое применение Все эти фигуры могут быть построены при помощи простой верёвки и значит эти знания очень пригодятся в повседневной жизни