Презентация на тему: Решение задач с помощью квадратных уравнений

Квадратные уравнения.презентация

Тема урока Решение задач с помощью квадратных уравнений.

Цель урокаПродолжить формирование навыка решений квадратных уравнений по формуле.Совершенствовать навык составления уравнения по условию задачи, умение проверять соответствие найденного решения условиям задачи.

Уравнения видаax2+bx+c=0, где a≠0называют квадратным уравнением.Если а=1, то уравнение называютприведенным квадратным уравнением.

В Греции математики овладели искусством решать квадратные уравнения путем использования геометрической алгебры. Примеры геометрического решения квадратных уравнений приводятся в знаменитой «Алгебре Мухаммеда аль-Хорезми»

Решим уравнение x2+10x=39Решим уравнение x2+10x=39 Построим квадрат ABCD со стороной х см и на его сторонах ВС и СD равные прямоугольники с высотой 5 см. M K F В С L А D N

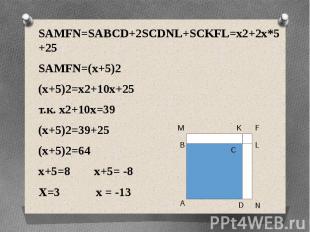
SAMFN=SABCD+2SCDNL+SCKFL=x2+2x*5+25SAMFN=SABCD+2SCDNL+SCKFL=x2+2x*5+25SAMFN=(x+5)2(x+5)2=x2+10x+25т.к. x2+10x=39(x+5)2=39+25(x+5)2=64х+5=8 х+5= -8Х=3 х = -13

Впервые отрицательные корни уравнений стал находить индийский математик Бхаскара ХII в., книга которого «Лилавати» являлась главным источником математических знаний на Востоке Впервые отрицательные корни уравнений стал находить индийский математик Бхаскара ХII в., книга которого «Лилавати» являлась главным источником математических знаний на Востоке

В Европе решение квадратных уравнений было изложено итальянским ученым Леонардо Фибоначчи в «Книге абака» (начало ХIII в.). В Европе решение квадратных уравнений было изложено итальянским ученым Леонардо Фибоначчи в «Книге абака» (начало ХIII в.). В середине XVI в. в общее правило решения квадратных уравнений при любых знаках коэффициентов было дано немецким математиком М. Штифелем

Решение квадратных уравнений по формуле.

Решение квадратного уравнения по формуле

Реши уравнения и выбери правильный ответ

Ответы

№ 1

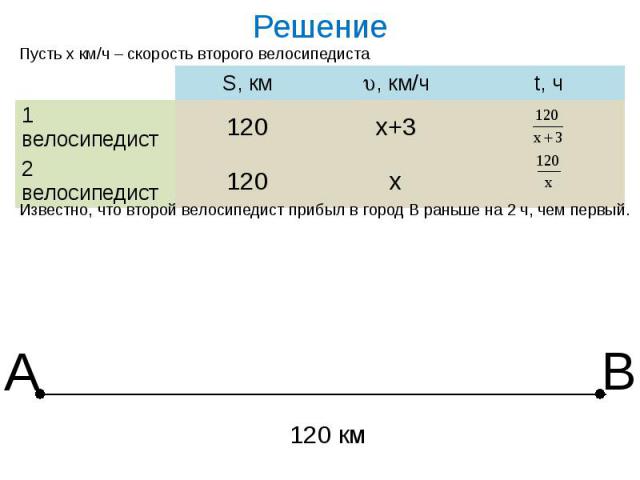
Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорость велосипедистов.Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорость велосипедистов.

Решение

Составим и решим уравнение:Умножим обе части этого уравнения на x(x+3)Число -15 противоречит смыслу задачиЕсли х=12, то х(х+3)≠0, верно12 км/ч – скорость второго велосипедиста15 км/ч – скорость первого велосипедиста

Реши самостоятельно

Из пунктов А и В навстречу друг другу одновременно вышли два пешехода. Скорость первого на 1 км/ч больше скорости второго, поэтому он прибыл в пункт В на 1 ч раньше, чем второй в пункт А. Найдите скорости пешеходов, если расстояние между пунктами А и В равно 20 км.

По условию задачи время движения первого пешехода на 1 ч меньше времени движения второго.

Число -5 противоречит смыслу задачиЕсли х=4, то х(х+1)≠0, верно4 км/ч – скорость второго пешехода5 км/ч – скорость первого пешехода

№ 2

Катер, собственная скорость которого 8 км/ч, прошёл по реке расстояние, равное 15 км, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.

Решение

РешениеЧисло -2 противоречит смыслу задачиЕсли х=2, то (8-х)(8+х)≠0, верно2 км/ч – скорость течения реки

Реши самостоятельно

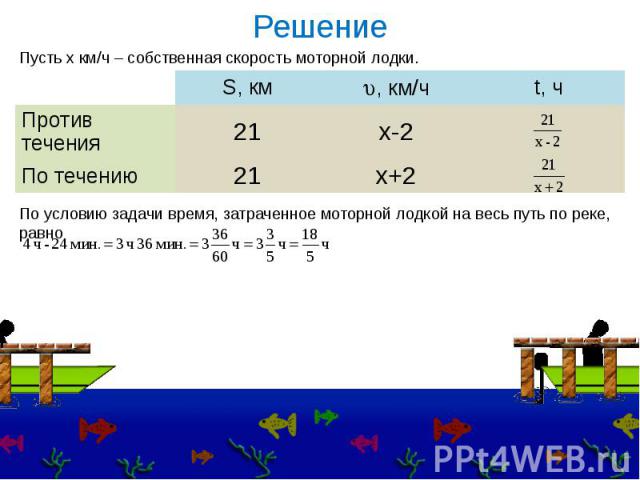
Расстояние между пристанями по реке равно 21 км. Моторная лодка отправилась от одной к другой и через 4 ч вернулась назад, затратив 24 мин. на стоянку. Найти собственную скорость лодки, если скорость течения реки равна 2 км/ч.

РешениеПо условию задачи время, затраченное моторной лодкой на весь путь по реке, равно

РешениеЧисло противоречит смыслу задачиЕсли х=12, то (х-2)(х+2)≠0, верно12 км/ч – собственная скорость моторной лодки