Презентация на тему: Последовательности

Последовательности 2011 Васильева Е.Е.

Продолжи ряд 1, 2, 3, 4, 5, 6 12, 10, 8, 6, 4 6, 9, 12, 15, 18, 21 2, 4, 8, 16, 32 1, 4, 16

Последовательности составляют такие элементы природы,которые можно пронумеровать

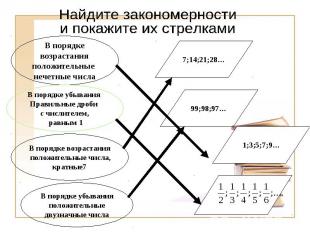
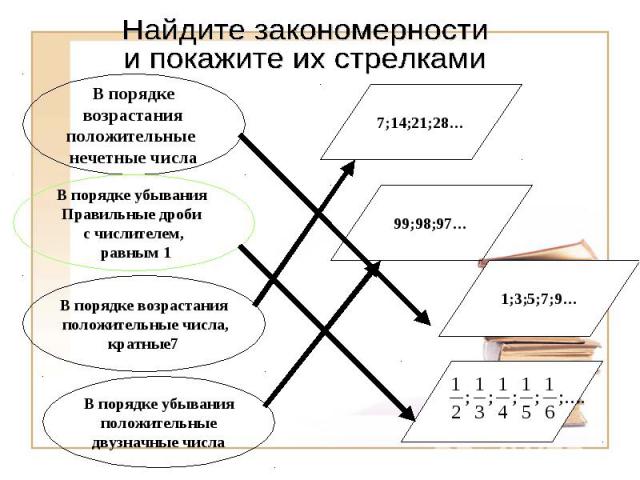
Найдите закономерностии покажите их стрелками

Определение Функцию y=f(x), определенную на множестве натуральных чисел xϵN (или его конечном подмножестве), называют числовой последовательностью и обозначают y=f(n), или y1,y2,…,yn,…. или (yn).

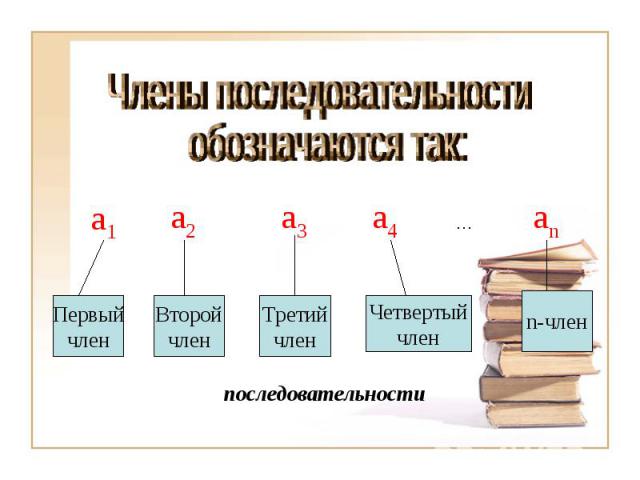
Числа y1, y2, …, yn называют членами последовательности, а член с номером n – ее n-членом, его еще называют общим членом.

Члены последовательности обозначаются так:

Задать числовую последовательность— это значит указать, как отыскивается тот или иной ее член, если известен номер занимаемого им   места.

Способы описания последовательности Последовательности можно задавать различными способами, среди которых особенно важны три: аналитическийсловесный рекуррентный

Формула1. Последовательность задана аналитически, если задана формула ее n-го члена: yn = f(n).Пример: yn = 2n – 1 Y1=2*1-1=1Y2=2*2-1=2Y3=2*3-1=5Y4=2*4-1=7Y5=2*5-1=9последовательность нечетных чисел: 1, 3, 5, 7, 9, …

Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность. Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, ….

РекурентныйРекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены.

Пример рекуррентного заданияПример 1. y1 = 3; yn = yn–1 + 4, если n = 2, 3, 4,….Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

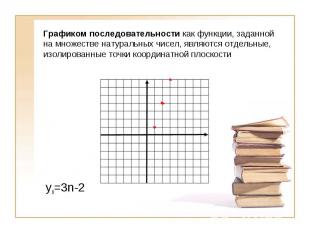
Графиком последовательности как функции, заданной на множестве натуральных чисел, являются отдельные, изолированные точки координатной плоскости

Последовательности заданы формулами1. Впишите пропущенные члены последовательности2. Укажите, какими числами являются члены этих последовательностей

По преданию, индийский царь Шерам, восхищенный  остроумием шахматной игры, призвал к себе изобретателя шахмат Сету и сказал ему: «Я желаю достойно вознаградить тебя ! Исполню любое твое желание…» Сета попросил положить на первую клетку доски 1 пшеничное зерно, на вторую – 2  зерна, на третью – 4 зерна и т. д.  Сколько нужно зерен ?  

Среднеазиатский математик Бернулли получил верный ответ:      18 446 744 073 709 551 615 зерен.Такое количество зерен пшеницы можно собрать лишь с урожая планеты, поверхность которой в 2000 раз больше поверхности Земли.

ПРОТОРГОВАЛСЯ ЛИ КУПЕЦ ? Некто продавал коня и просил за него 1000 рублей. Купец сказал, что цена велика, "Хорошо,-ответил продавец, если ты говоришь, что конь дорого стоит, то возьми его себе даром, а заплати только за одни гвозди на его подковах, а гвоздей на его каждой подкове по 6 штук, и будешь ты мне за них платить таким образом: за первый гвоздь полушку, за второй - две полушки, за третий 4 полушки, и так далее за все гвозди: за каждый в два раза больше чем предыдущий". Купец согласился, проторговался ли купец?

РЕШЕНИЕ:всего гвоздей 24 штуки, за все гвозди купец должен заплатить 1 + 2 + 2*2 + 2*2*2+ +...+2*2*...*2 полушек23 раза и того получаем 41943 рубля и 15 полушек.

Свойства числовых последовательностей Числовая последовательность называется возрастающей, если каждый ее член больше предыдущего, иными словами, если для всякого  n > 1  верно неравенство  an > a n – 1.

ПримерПоследовательность кубов натуральных чисел1,8,27

УБЫВАЮЩАЯ Числовая последовательность называется убывающей, если каждый ее член (кроме первого) меньше предыдущего, иными словами, если для всякого  n > 1  верно неравенство  an < a n – 1.

Пример

Монотонность Вместе возрастающие и убывающие последовательности называются монотонными последовательностями.

Определить монотонность1)-1,-4,-9,-16….2)-1,0,1,2….3)-1,1,-1,1

Ограниченность сверху Определение. Последовательность  a1,  a2,  a3,  … называется ограниченной сверху, если для ее такое число  M,  что неравенство  an

Пример1,-1,-3,-5Ограничена сверху М =1

Ограниченность снизуОпределение. Последовательность  a1,  a2,  a3,  … называется ограниченной снизу, если для ее такое число  m,  что неравенство  an >m  выполняется для всех номеров  n.

ПримерОграничена и сверху и снизуМ=1M=0

Упражнение 1Укажите номер функции, являющейся числовой последовательностью

Упражнение 2Найдите первые пять членов последовательности заданной рекуррентноY1=2Yn=yn-1+5

Упражнение 3

Упражнение 4Укажите номер убывающей последовательности

Упражнение 5Является ли ограниченной последовательность