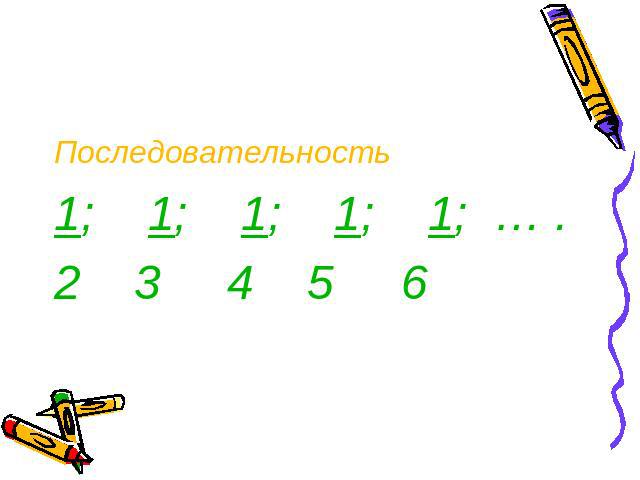Презентация на тему: Последовательности

Тема урока:Последовательности

Выпишем в порядке возрастания положительные четные числа Первое такое число равно ?, второе - ?, третье - ?, четвёртое - ? и т.д.

Получим последовательность 2; 4; 6; 8; … .На пятом месте в этой последовательности будет число ?, на десятом - ?, на сотом - ?

Для любого натурального числа п можно указать соответствующее ему положительное чётное число; оно равно 2п.

Еще одна последовательность Выпишем в порядке убывания правильные дроби с числителем, равным 1: Какие это дроби?

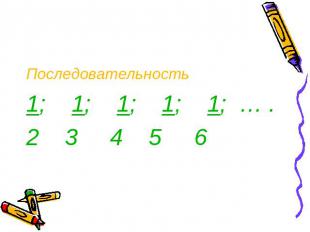
Последовательность1; 1; 1; 1; 1; … .2 3 4 5 6

Для любого натурального числа п можно указать соответствующую дробь, стоящую в этой последовательности на п- м месте; она равна 1 . п + 1Так на шестом месте должна стоять дробь ?, на тридцатом - ?, на тысячном - ?

Числа, образующие последовательность, называют членами последовательности.Члены последовательности обозначаются буквами с индексами, указывающими порядковый номер члена, например: а 1, а 2, а 3, а 4, и т.д.(читают так: «а первое , а второе, а третье , а четвертое и т.д.)

Член последовательности с номером п, или п- й член последовательности, обозначают а п, а саму последовательность - (а п)

Последовательности, содержащие бесконечно много членов, называются бесконечными.Последовательности, содержащие конечное число членов, называют конечными. Например: конечной является последовательность двузначных чисел 10; 11; 12; 13; …; 98; 99.

Часто последовательность задают с помощью формулы п- го члена последовательности

Примеры: